§3. Координаты центра тяжести некоторых простых фигур.

1. Центр тяжести треугольника. Центр тяжести треугольника лежит в точке пересечения его медиан (рис. 5). Координаты центра тяжести треугольника представляют собой среднее арифметическое из координат его вершин: x _c =1/3(x₁+x₂+x₃); y _c =1/3(y₁+y₂+y₃).

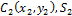
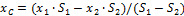
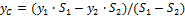
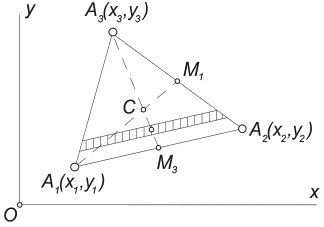
Рис. 5. Центр тяжести треугольника

2. Центр тяжести прямоугольника. Центр тяжести прямоугольника лежит в точке пересечения его диагоналей (рис. 6). Координаты центра тяжести прямоугольника рассчитываются по формулам: x _c =b/2; y _c =h/2.

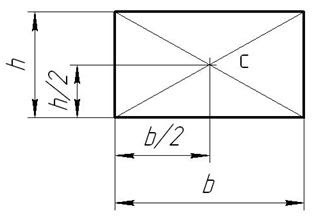
Рис. 6. Центр тяжести треугольника

3. Центр тяжести полукруга. Центр тяжести полукруга лежит на оси симметрии (рис. 7). Координаты центра тяжести полукруга рассчитываются по формулам: x _c =D/2; y _c =4R/3π.

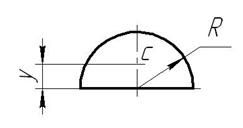
Рис. 7. Центр тяжести полукруга

4. Центр тяжести круга. Центр тяжести круга лежит в центре (рис. 8). Координаты центра тяжести круга рассчитываются по формулам: x _c =R; y _c =R.

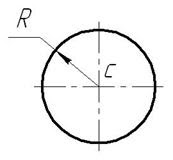
Рис. 8. Центр тяжести круга

Вопросы для самопроверки:

- Что называется центром параллельных сил?

- Что называется центром тяжести тела?

- Почему силы притяжения Земле, действующие на точку тела, можно принять за систему параллельных сил?

- Запишите формулу для определения положения центра тяжести неоднородных и однородных тел, формулу для определения положения центра тяжести плоских сечений?

- Запишите формулу для определения положения центра тяжести простых геометрических фигур: прямоугольника, квадрата, трапеции и половины круга?

- Как используются свойства симметрии при определении центров тяжести тел?

- В чем состоит сущность способа отрицательных площадей?

- Каким графическим построением можно найти центр тяжести треугольника?

- Запишите формулу, определяющую центр тяжести треугольника.

⇐ Предыдущая 12