
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
§ 7. Дифференциальные уравнения второго порядка
§ 7. Дифференциальные уравнения второго порядка
Определение. Дифференциальным уравнением второго порядка называется уравнение, которое связывает независимую переменную x, неизвестную функцию y и первую и вторую производные от этой функции:
F (x, y, y', y'') = 0.
Определение. Общим решением дифференциального уравнения второго порядка называется функция
y = φ (x, C1, C2), которая удовлетворяет дифференциальное уравнение при произвольных значениях C1 и C2.
Любое частное решение дифференциального уравнения получается из общего решения при определенных значениях C1 и C2 и удовлетворяет определенным начальным условиям. Начальными условиями для дифференциального уравнения второго порядка является задание значений функции и ее первой производной в некоторой точке x0:
 и
и 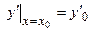
Задача Коши для дифференциального уравнения второго порядка подразумевает
нахождение частного решения дифференциального уравнения, удовлетворяющее начальным условиям.
Геометрический смысл частного решения — это интегральная кривая, проходящая через точку (x0, y0) в данном направлении, то есть, задан угловой коэффициент касательной к интегральной кривой.
§ 8. ДУ второго порядка, допускающие понижение порядка
Рассмотрим три вида ДУ второго порядка, которые можно преобразовать к разным видам ДУ первого порядка, т. е. понизить их порядок. Сведём эти уравнения в таблицу, указав их общий вид, характерные особенности и способы решения (способы понижения степени).
| Общий вид ДУ | 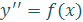
| 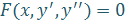
| 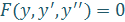
|
| Характерные особенности | Повторное интегрирование правой части | В ДУ в явном виде отсутствует искомая функция у | В ДУ в явном виде отсутствует независимая переменная х |
| Замена, приводящая к понижению порядка | - | 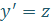
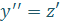
| 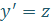 , где , где 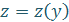
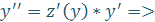
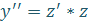
|
| Вид ДУ после понижения порядка | 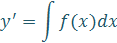
| 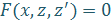
| 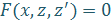
|
| Пример | Пример 1.
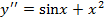
| Пример 2.
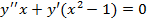
| Пример 3.
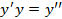 , ,
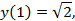
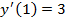
|
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|