
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Расчёт плоской статически неопределимой рамы методом сил
Шифр 530
Задача 7
Расчёт плоской статически неопределимой рамы методом сил
Для рамы (рис. 1) требуется:
а) построить эпюры изгибающих моментов, поперечных и продольных сил, раскрыв статическую неопределимость;
б) проверить правильность раскрытия статической неопределимости.
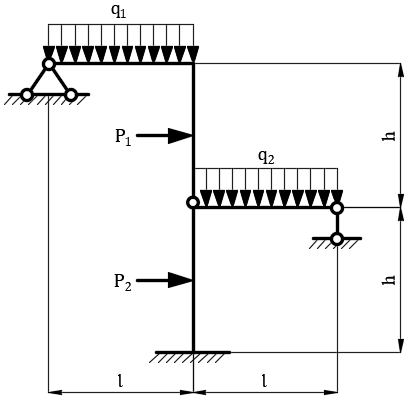
Рис. 1. Заданная схема статически неопределимой рамы
Исходные данные:
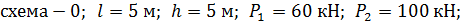
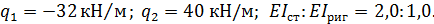
Решение
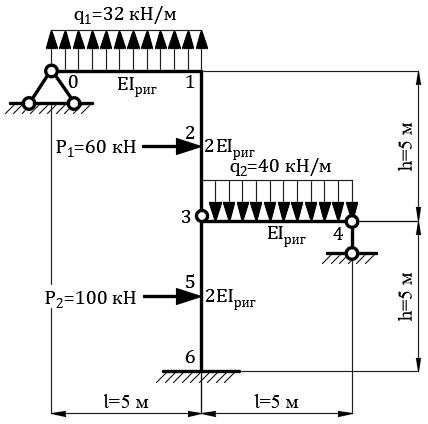
Рис. 2. Расчетная схема статически неопределимой рамы
1. Определяем степень статической неопределимости рамы:
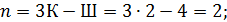
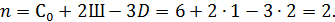
Обозначения контуров и шарниров к первой формуле приведены на рис. 3, а, а обозначения опорных связей, шарниров и дисков ко второй формуле – на рис. 3, б.
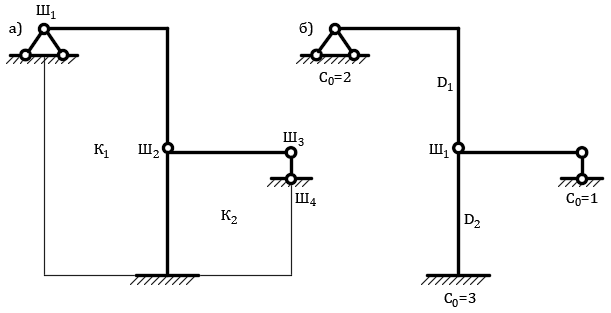
Рис. 3. Определение степени статической неопределимости
2. Выбираем основную систему метода сил (ОС). Для этого устраняем две лишние связи (рис. 4).
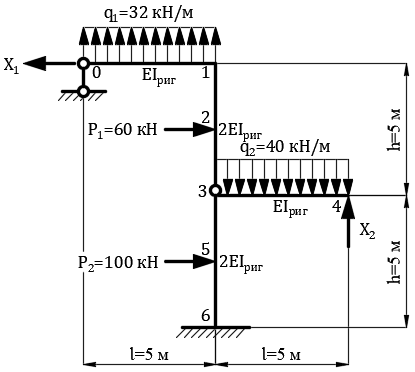
Рис. 4. Основная система
3. Записываем канонические уравнения метода сил:
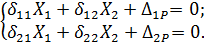
4. Вычисляем коэффициенты 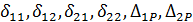 . Для этого строим в ОС эпюры изгибающих моментов
. Для этого строим в ОС эпюры изгибающих моментов 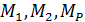 от
от 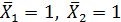 и заданной нагрузки соответственно (рис. 5), для чего определяем опорные реакции для каждого вида загружения.
и заданной нагрузки соответственно (рис. 5), для чего определяем опорные реакции для каждого вида загружения.
Эпюра моментов от внешней нагрузки

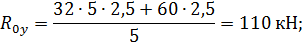
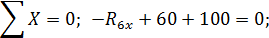
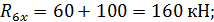
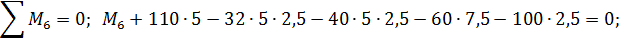
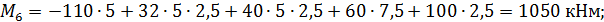
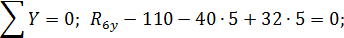
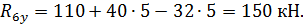
Эпюра моментов 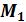 от единичной силы
от единичной силы 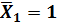
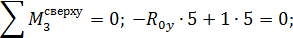
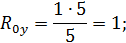
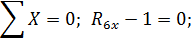
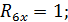
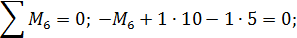

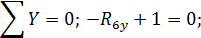
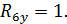
Эпюра моментов 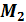 от единичной силы
от единичной силы 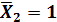
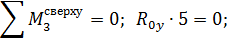
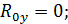
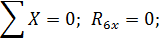
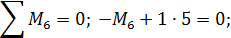
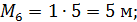
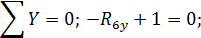
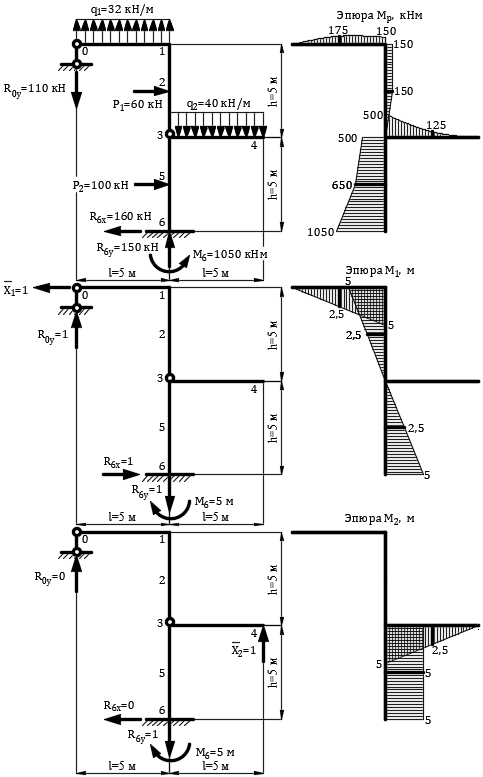
Рис. 5. Эпюры изгибающих моментов в основной системе
Вычисление перемещений 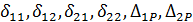 выполняем, перемножая соответствующие эпюры по правилу Верещагина:
выполняем, перемножая соответствующие эпюры по правилу Верещагина:
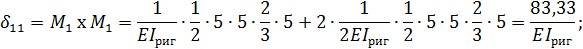
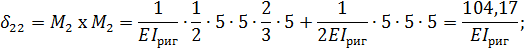
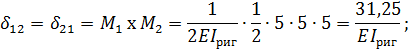
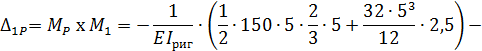

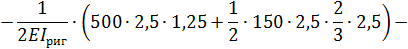
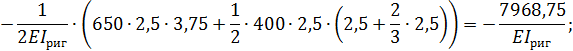
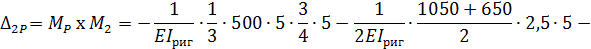
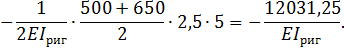
5. Для проверки правильности предыдущих вычислений строим суммарную единичную эпюру 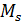 (рис. 6).
(рис. 6).
Вычисляем 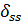 и
и 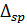 :
:
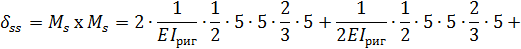
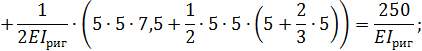
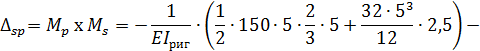

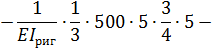

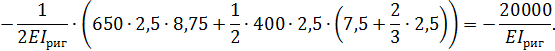
Вычисляем суммы соответствующих коэффициентов:
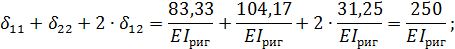
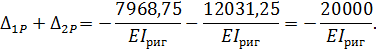
Условия выполняются:
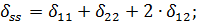
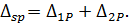
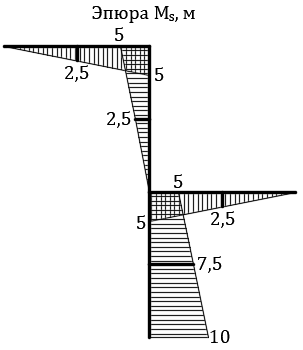
Рис. 6. Суммарная единичная эпюра 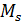
6. Подставляем найденные значения перемещений в систему канонических уравнений и умножаем всё на 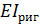 :
:
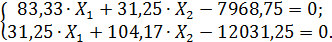
Решая эту систему, получаем:
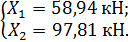
7. Построение окончательной эпюры изгибающих моментов 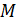 (рис. 7) производим по формуле:
(рис. 7) производим по формуле:
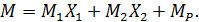

Рис. 7. Эпюры 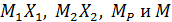
8. Выполняем деформационную проверку полученного решения. Для этого перемножаем окончательную эпюру 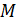 на эпюру
на эпюру 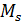 :
:
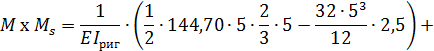
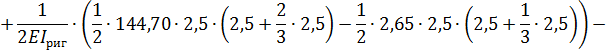
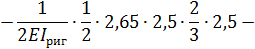
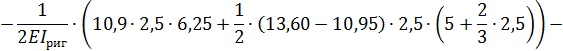
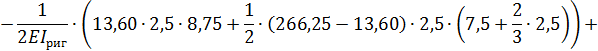
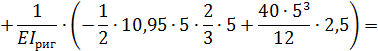

Относительная погрешность:
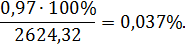
9. Строим эпюру поперечных сил.
Вычисляем значения поперечных сил на границах участков.
Участки 1-2, 2-3, 3-5 и 5-6, где 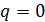 :
:
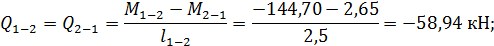
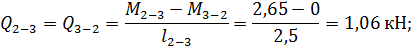
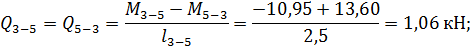
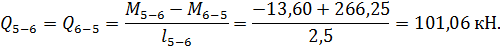
Участок 0-1, где 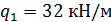 :
:
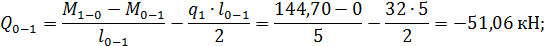
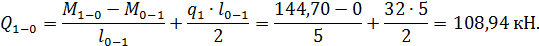
Участок 3-4, где 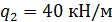 :
:
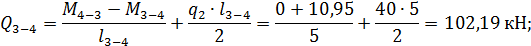
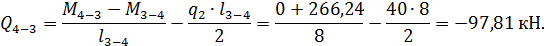
Эпюра поперечных сил 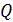 , построенная по найденным значениям, представлена на рис. 8.
, построенная по найденным значениям, представлена на рис. 8.

Рис. 8. Эпюра поперечных сил 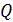
На участках рамы 0-1 и 3-4 имеются поперечные сечения, в которых 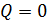 , поэтому для этих сечений необходимо вычислить экстремальные значения изгибающих моментов. Положение этих сечений найдём, используя дифференциальную зависимость:
, поэтому для этих сечений необходимо вычислить экстремальные значения изгибающих моментов. Положение этих сечений найдём, используя дифференциальную зависимость:
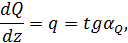
где 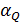 – угол наклона эпюры
– угол наклона эпюры 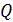 .
.
Тогда:
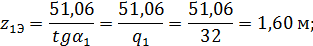
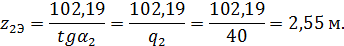
Экстремальные значения изгибающего момента вычислим с помощью интегрального соотношения между М и Q:
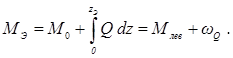
Здесь 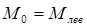 – изгибающий момент в начале (в левом сечении) рассматриваемого участка;
– изгибающий момент в начале (в левом сечении) рассматриваемого участка; 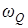 – «площадь» эпюры поперечных сил от начала участка до сечения, где
– «площадь» эпюры поперечных сил от начала участка до сечения, где 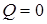 .
.
Тогда:
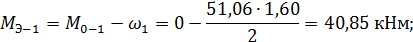
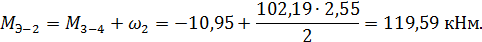
10. Строим эпюру продольных сил N. Вырезаем узлы рамы 1 и 3и прикладываем в сечениях известные из эпюры Q поперечные силы и неизвестные продольные силы. Направления поперечных сил указываем в соответствии с принятым правилом знаков, а неизвестные продольные 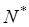 покажем «растягивающими» (рис. 9).
покажем «растягивающими» (рис. 9).
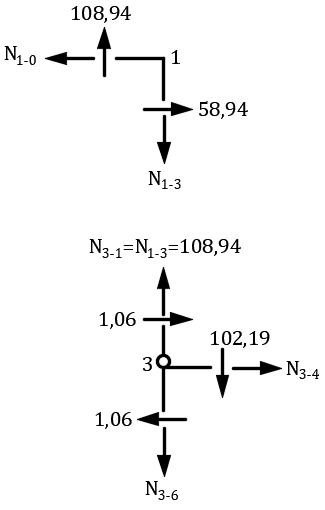
Рис. 9. Схемы узлов рамы для определения продольных сил
Из условий равновесия узла 1 получаем:
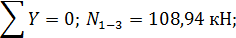
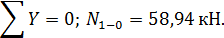
Из условий равновесия узла 3 получаем:
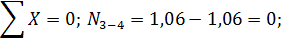
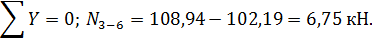
Эпюра N, построенная по найденным значениям, представлена на рис. 10.
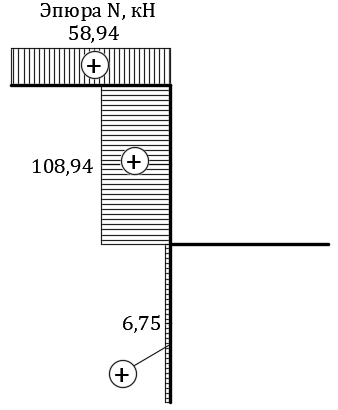
Рис. 10. Эпюра продольных сил N
11. Выполняем статическую проверку всех построенных эпюр.
На рис. 11 показана расчётная схема рамы с отброшенными внешними связями и приложенными вместо них реакциями, значения и направления которых взяты с эпюр М, Q и N в соответствии с правилами знаков внутренних усилий.
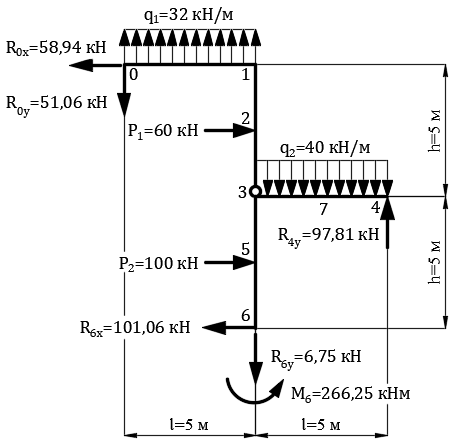
Рис. 11. Расчётная схема рамы с отброшенными опорными связями
Составляем уравнения равновесия:
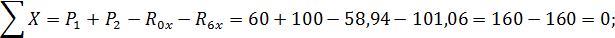
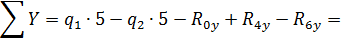
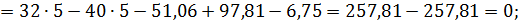
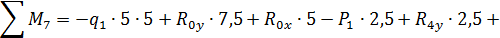
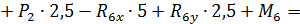
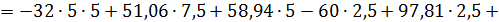
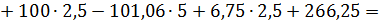
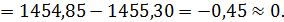
Таким образом, все проверки подтверждают правильность раскрытия статической неопределимости.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|