
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема: Разложение вектора по трем некомпланарным векторам.
Уважаемый обучающийся, все работы выполняются в рабочих тетрадях по математике. Работа выполняется синей пастой. Построения выполнять простым карандашом.
Тема: Разложение вектора по трем некомпланарным векторам.
Цель: изучить теорему о разложении вектора по трём некомпланарным векторам; научиться применять полученные знания при решении задач.
Решенные примеры писать не нужно. Они как образец для решения д/з.
1. Записать определения, теорему. Рассмотреть доказательство теоремы.
Аналогично тому, как на плоскости любой вектор можно разложить по двум неколлинеарным векторам, наверняка, в пространстве любой вектор можно разложить по трём некомпланарным векторам.
Определение. Если вектор 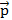 представлен в виде:
представлен в виде: 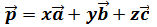
где x, y, z – некоторые числа, то говорят, что вектор 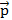 разложен по векторам
разложен по векторам 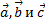 . Числа x, y, z называются коэффициентами разложения.
. Числа x, y, z называются коэффициентами разложения.
Запишем теорему. Любой вектор можно разложить по трём некомпланарным векторам, причём коэффициенты разложения определяются единственным образом.
 Докажем эту теорему для некомпланарных векторов
Докажем эту теорему для некомпланарных векторов 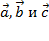 .
.
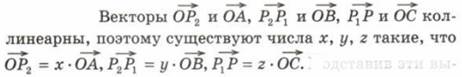
Получаем:
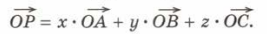
Т. к. 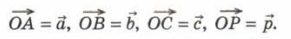 , то
, то 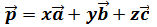
Осталось только доказать, что коэффициенты разложения x, y, z определяются единственным образом.
Допустим, что кроме полученного нами разложения есть ещё одно, в котором коэффициенты разложения равны x1, y1, z1.
Вычтем второе разложение из первого.
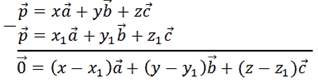
В разложении нулевого вектора по трём некомпланарным ненулевым векторам все коэффициенты разложения должны быть равны нулю.
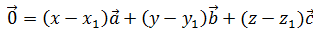
Отсюда соответственно равны коэффициенты:
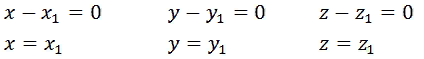
А это противоречит нашему допущению о том, что коэффициенты второго разложения вектора 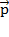 отличны от коэффициентов первого разложения.
отличны от коэффициентов первого разложения.
Отсюда получаем, что коэффициенты разложения x, y, z определяются единственным образом. Что и требовалось доказать.
2. Выполним несколько заданий.
№ 1 а
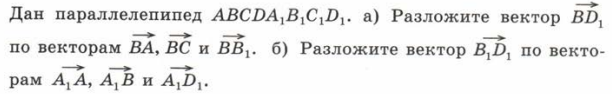
Решение:
а) Пользуясь правилом параллелепипеда сложения трёх некомпланарных векторов, нетрудно заметить, что 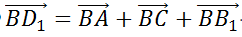 Таким образом мы разложили вектор
Таким образом мы разложили вектор 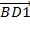 по данным векторам. Причём каждый коэффициент данного разложения равен единице.
по данным векторам. Причём каждый коэффициент данного разложения равен единице.
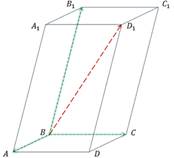
№ 2.
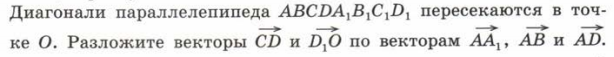
Решение: Разложим вектор 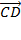 .
.
Сразу можно отметить, что 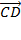 =
= 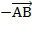 . Поэтому в разложении этого вектора по данным векторам коэффициенты разложения при векторах
. Поэтому в разложении этого вектора по данным векторам коэффициенты разложения при векторах 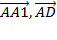 = 0, а при векторе
= 0, а при векторе 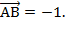
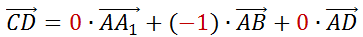
3. Домашнее задание.
№ 1 б
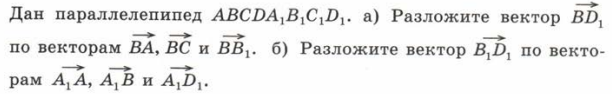
№ 2.
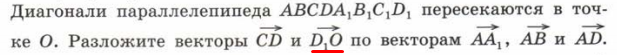
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|