
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Применение непрерывности. Метод интервалов
Применение непрерывности. Метод интервалов
На свойстве непрерывности функций основан метод решения неравенств, который называется методом интервалов.
Пример 1. Решите неравенство 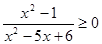 .
.
Решение.
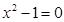 ;
;
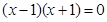 ;
;
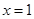 ;
; 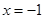 .
.
Функция  непрерывна в каждой точке своей области определения и обращается в нуль в точках
непрерывна в каждой точке своей области определения и обращается в нуль в точках 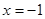 и
и 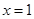 . Это «нули» функции.
. Это «нули» функции.
 ;
;
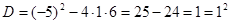 ;
;
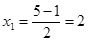 ;
; 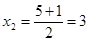
Область определения функции – вся числовая прямая, за исключением точек 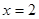 и
и 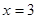 . Это точки разрыва функции.
. Это точки разрыва функции.
Исходное неравенство 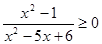 принимает вид
принимает вид 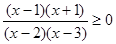 .
.
Этот неравенство эквивалентно неравенству 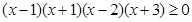 , т. е. предыдущее неравенство, переписываем в одну строчку.
, т. е. предыдущее неравенство, переписываем в одну строчку.
Особенностью решения неравенств методом интервалов является то, что во всех скобках переменная х должна стоять в начале и возле неё не должно быть никаких коэффициентов (чисел). Если возле х стоит число, то его мы обязательно выносим за скобки.
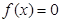 при
при 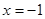 ,
, 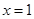 ,
, 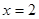 ,
, 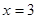 .
.
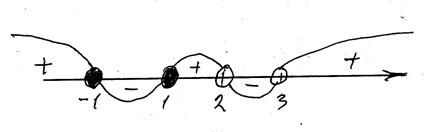
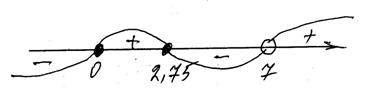
На рисунке изображаем точки 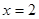 ,
, 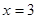 , находящиеся в знаменателе, светлыми, а точки
, находящиеся в знаменателе, светлыми, а точки 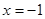 ,
, 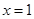 , находящиеся в числителе – тёмными.
, находящиеся в числителе – тёмными.
Правый промежуток всегда принимает положительные значения, остальные принимают поочерёдно отрицательные и положительные значения.
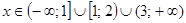 .
.
Ответ: 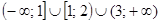 .
.
Пример 2. Решите неравенство: 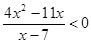 .
.
Решение.
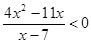 ;
;
 ;
;
В верхних скобках возле х стоит коэффициент 4, который выносим за скобки.
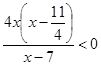 ;
;
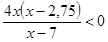 ;
;
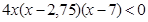 ;
;
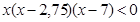 ;
;
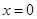 ;
; 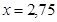 ;
; 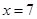 .
.
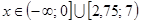 .
.
Ответ: 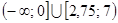 .
.
Домашнее задание.
№ 244. Решите неравенство методом интервалов.
б) 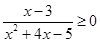 ; г)
; г) 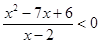 .
.
№ 245. Решите неравенство методом интервалов.
а) 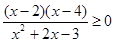 ; г)
; г) 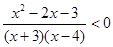 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|