
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Лекция 1. «Целые и рациональные числа. Действительные числа»
Лекция 1. «Целые и рациональные числа. Действительные числа»
Числа 1, 2, 3, …, употребляемые при счете предметов, образуют множество натуральных чисел. (только положительные числа)
Это множество обозначается буквой N.
Например, запись 27Є N читается: «27 принадлежит множеству натуральных чисел».
Ноль не является натуральным числом.
Натуральные числа, противоположные им числа и число нуль составляют множество целых чисел.
Это множество обозначается буквой Z.
Например, запись -47Є Z читается: «-47 принадлежит множеству целых чисел».
Виды дробей:
1. Обыкновенная дробь (простая дробь) – запись рационального числа в виде отношения двух чисел  . Делимое m называется числителем дроби, а делитель n – знаменателем дроби.
. Делимое m называется числителем дроби, а делитель n – знаменателем дроби.
1. 1. Правильная дробь – у которой числитель меньше знаменателя.  .
.
1. 2. Неправильная дробь – у которой числитель больше или равен знаменателю.  .
.
2. Смешанная дробь (смешанное число) – называется дробь, записанная в виде целого числа и правильной дроби и понимается как сумма этого числа и дроби. 3  .
.
3. Десятичная дробь – сначала целая часть, затем разделитель целой и дробной части точка или запятая и затем дробная часть. 3, 52.
4. Периодическая дробь – это бесконечная десятичная дробь, у которой, начиная с некоторого десятичного знака, повторяется одна и та же цифра или группа цифр.
Например, 1/3=0, 333333…=0, (3) («ноль целых три в периоде»)
Целые и дробные числа (положительные и отрицательные) составляют множество рациональных чисел.
Это множество обозначается буквой Q.
Например, запись -3, 5Є Q читается: «-3, 5 принадлежит множеству рациональных чисел».
Всякое рациональное число можно представить в виде дроби,  , где m Є Z, n Є N. Например: 5=5/1=10/2=15/3, 0, 7=7/10, -4=-4/1.
, где m Є Z, n Є N. Например: 5=5/1=10/2=15/3, 0, 7=7/10, -4=-4/1.
Каждое рациональное число может быть представлено в виде бесконечной десятичной периодической дроби.
Например: 5=5, 000…, 1/8=0, 125000…, 1/3=0, 333…, -5/11=0, 4545…, -4, 6=4, 6000….
Иррациональные числа – это числа, которые не является рациональными, то есть не могут быть представлены в виде обыкновенной дроби  . Иррациональное число может быть представлено в виде бесконечной непериодической десятичной дроби.
. Иррациональное число может быть представлено в виде бесконечной непериодической десятичной дроби.
Например: 1, 254684125648…, П ≈ 3, 145926…, √ 2=1, 41421…
Множество действительных чисел состоит из рациональных и иррациональных чисел.
Это множество обозначается буквой R.
Например, запись -3, 5Є R читается: «-3. 5 принадлежит множеству действительных чисел».
Множество действительных чисел называют также числовой прямой. Каждой точке координатной прямой соответствует некоторое действительное число, и каждому действительному числу соответствует точка на координатной прямой.
Пример 1: 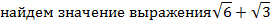
Воспользуемся калькулятором:

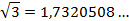
Найдем значение данного выражения с точностью до единиц.
Округлим полученные результаты до десятых:
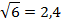
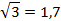
Тогда получаем:
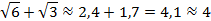
Найдем значение данного выражения с точностью до десятых.
Округлим полученные результаты до сотых:
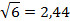
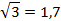 3
3
Тогда получаем:
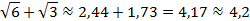
Найдем значение данного выражения с точностью до сотых.
Округлим полученные результаты до тысячных:

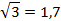 32
32
Тогда получаем:
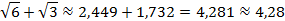 и т. д.
и т. д.
Задание:
1. Записать в виде десятичной дроби:  ,
,  ,
, 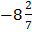 .
.
2. Вычислить: 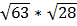 ,
,  .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|