
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
задание профильного ЕГЭ по математике
Наше занятие сегодня посвящено важной теме
задание профильного ЕГЭ по математике
мы с вами рассмотрим несколько способов решения различных уравнений, используя в том числе и материал предыдущего занятия.
Решить уравнение и найдите все корни этого уравнения, принадлежащие промежутку [1/2; 3]
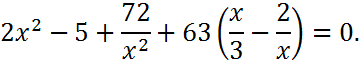
Способ 1. Приведение уравнения к уравнению четвертой степени. Умножим обе части уравнения на х2
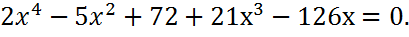
решаем уравнение, используя схему Горнера
| |
| |
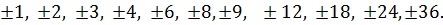
Выпишем коэффициенты уравнения, расположенные по убыванию степеней переменной x, в таблицу.
|
| -5 | -126 | |||
| Х=2 | -36 | ||||
| Х=-3 | -12 |
|
Мы понизили степень уравнения и получили уравнение второй степени.
2Х2 +19 х -12 = 0
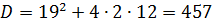
Корнями квадратного уравнения будут числа 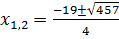
Ответ:  .
.
Способ 2. Замена переменной.
Данный метод несколько искусственный и требует некоторого опыты в применении. Рассмотрим отдельно разность в скобках.
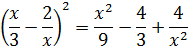
Выполним группировку
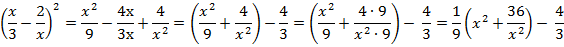
Мы получили
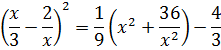
Умножим обе части выражения на 9:
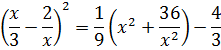
Выразим сумму в скобках в правой части равенства
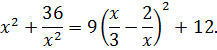
Зачем мы это Делали? Обратите, пожалуйста, внимание на само уравнение, точнее, подчеркнутую часть

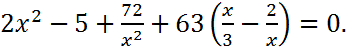
Получили, что
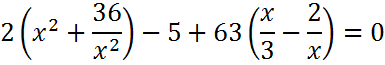
Тогда
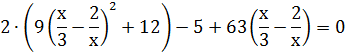
В результате получим уравнение, приводимое к квадратному
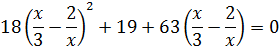
Сделаем замену переменной: 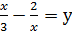
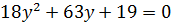
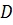 = 512 и
= 512 и 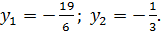
Выполним обратную замену переменной
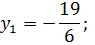
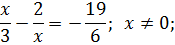
Умножим обе части уравнения на х
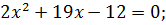

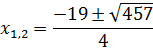
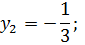
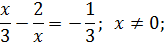
Умножим обе части уравнения на х
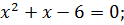
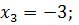

Ответ:  .
.
Найдем все корни этого уравнения, принадлежащие промежутку 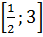
Числа 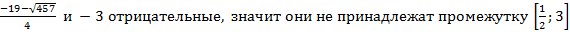 .
.
Число 2 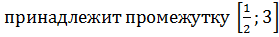 .
.
Р 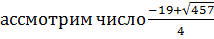
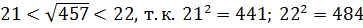 , тогда
, тогда
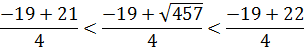
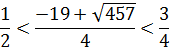
значит число 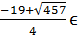
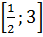
Ответ:
а) 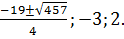
б) 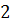 ;
; 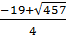
Задачи для самостоятельного решения
1. Решить уравнение и найдите все корни этого уравнения, принадлежащие промежутку [0, 25; 6, 9]
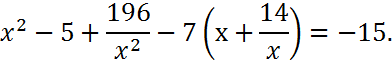
2. Решить уравнение и найдите все корни этого уравнения, принадлежащие промежутку [-10; 0, 5]
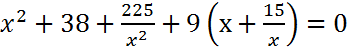
Решить неравенство: 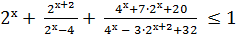
Решение: Сделаем замену переменной 2х = у, у > 0, учитывая, что
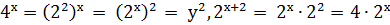 ,
,
Получаем: 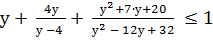
ОДЗ:
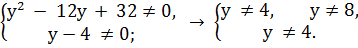
Упростим неравенство, приведя все к общему знаменателю.
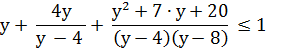
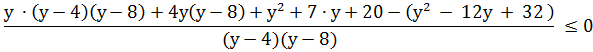
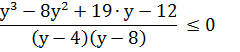
Решим неравенство методом интервалов. Для разложения на множители числителя используем схему Горнера. Выпишем коэффициенты уравнения, расположенные по убыванию степеней переменной x, в таблицу.
|
| -8 | -12 | ||
| У = 1 | -7 | |||
|
|
|
|
|
|
Корнями квадратного уравнения у2 – 7у + 12 = 0 будут числа 3 и 4.
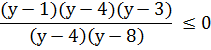
По методу интервалов

Тогда 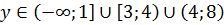
С учетом ОДЗ и 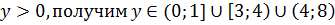
Так как 2х = у, тогда если 1 = 2х, то х = 0; если 4 = 2х, то х = 2; если 8 = 2х, то х = 3; если 3 = 2х, то х = 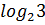 . Получаем
. Получаем
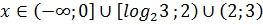
Ответ: 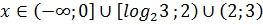
Задания для самостоятельного решения
1) 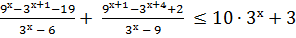
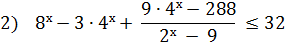
3) 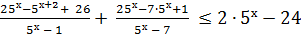
Ответы на задания принести на занятие
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|