2 Понятие корреляционного поля

2 Понятие корреляционного поля

Для визуального анализа корреляционной связи служит диаграмма рассеивания.

На рисунке 1 мы видим точечный график, данные которого дают основания предположить, что между двумя признаками х и у существует отрицательная линейная корреляционная связь: величина у в среднем приблизительно линейно убывает с ростом х.

Могут быть и другие варианты распределения, когда изменение переменной у никак не зависит от изменений х. Либо зависимость есть, но она не линейна.

Степень близости точек на диаграмме рассеивания к некоторой функциональной зависимости (например, к прямой линии) принято называть теснотой корреляции.

Рис 1. Диаграмма рассеивания

3. Измерение тесноты связи

Измерителем тесноты линейной корреляции служит выборочный (эмпирический) коэффициент корреляции.

Его принято обозначать символом r_ху или просто r

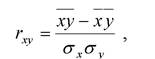
Коэффициенты корреляции — удобный показатель связи, получивший широкое применение в практике. К их основным свойствам необходимо отнести следующие:

Коэффициенты корреляции способны характеризовать только линейные связи, т. е. такие, которые выражаются уравнением линейной функции. При наличии нелинейной зависимости между варьирующими признаками следует использовать другие показатели связи.
Значения коэффициентов корреляции – это отвлеченные числа, лежащее в пределах от —1 до +1, т. е. -1 < r < 1.
При независимом варьировании признаков, когда связь между ними отсутствует,
r = 0.
При положительной, или прямой, связи, когда с увеличением значений одного признака возрастают значения другого, коэффициент корреляции приобретает положительный (+) знак и находится в пределах от 0 до +1, т. е. 0 < r < 1.
При отрицательной, или обратной, связи, когда с увеличением значений одного признака соответственно уменьшаются значения другого, коэффициент корреляции сопровождается отрицательным (–) знаком и находится в пределах от 0 до –1, т. е. -1 < r < 0.
Чем сильнее связь между признаками, тем ближе величина коэффициента корреляции к |1|. Если r = 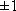, то корреляционная связь переходит в функциональную, т. е. каждому значению признака Х будет соответствовать одно или несколько строго определенных значений признака Y.
Только по величине коэффициентов корреляции нельзя судить о достоверности корреляционной связи между признаками. Этот параметр зависит от числа степеней свободы k = n –2, где: n – число коррелируемых пар показателей Х и Y. Чем больше n, тем выше достоверность связи при одном и том же значении коэффициента корреляции.

В практической деятельности, когда число коррелируемых пар признаков Х и Y не велико, то при оценке зависимости между показателями используется следующую градацию:

1) высокая степень взаимосвязи – значения коэффициента корреляции находится в пределах от 0, 7 до 0, 99;

2) средняя степень взаимосвязи – значения коэффициента корреляции находится в пределах от 0, 5 до 0, 69;

3) слабая степень взаимосвязи – значения коэффициента корреляции находится от 0, 2 до 0, 49.

Модификацией уже представленной формулы r_xy является формула Пирсона:

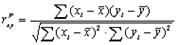
Данная формула позволяет произвести расчеты в уже известных нам (из темы «Средние величины и показатели вариации») вспомогательных таблицах.

⇐ Предыдущая 12