Задача 617.

Алгебра

Шестнадцатое февраля

Тема. Решение задач с помощью дробных рациональных уравнений

Должны знать: алгоритм решения задач с помощью дробных рациональных уравнений;

Должны уметь: формировать у учащихся умения составлять дробное рациональное уравнение по условию задачи; решать задачи с помощью дробных рациональных уравнений.

Задание

1. Повторите о с н о в н ы е э т а п ы решения текстовой задачи алгебраическим методом:

1. Анализ условия задачи и его схематическая запись.

2. Перевод естественной ситуации на математический язык (построение математической модели: введение переменной и составление дробного рационального уравнения).

3. Решение полученного уравнения.

4. Интерпретация полученного результата.

2) Посмотреть фрагмент урока по ссылке https: //youtu. be/7T4gJ22saMU

Рассмотрим примеры задач (прикреплены)

Задача 617.

Р е ш е н и е

Пусть х – числитель обыкновенной дроби, тогда (х + 3) – её знаменатель. Увеличив числитель на 7, а знаменатель на 5, мы получили дробь 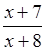. Зная, что дробь увеличилась на 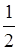, составим и решим уравнение:

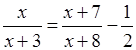; ОДЗ: х ≠ –3; х ≠ –8.

Общий знаменатель 2(х + 3)(х + 8).

2х(х + 8) = 2(х + 7)(х + 3) – (х + 3)(х + 8);

2х² + 16х = 2х² + 20х + 42 – х² – 11х – 24;

х² + 7х – 18 = 0.

х₁+х₂=-7.

х₁ * х₂= -18

По теореме, обратной теореме Виета, х₁ = 2, х₂ = –9. Смыслу задачи удовлетворяет только х = 2, тогда дробь равна .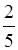

О т в е т: .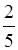

Обращаем внимание, что исходное уравнение можно было записать и по-другому:

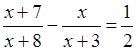(из большего значения вычитаем меньшее и получаем разницу) или .

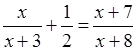3. Домашнее задание. Решить № 632 и задачу 1 по предложенным образцам.

Задача 1

Числитель обыкновенной дроби на 4 меньше её знаменателя. Если к числителю этой дроби прибавить 19, а к знаменателю 28, то она увеличится на 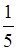. Найдите эту дробь.

В тетради записываем число:
Шестнадцатое февраля

Домашняя работа

Решение задач с помощью дробных рациональных уравнений

Результаты выполненной работы выполнить до следующего урока (17 февраля) включительно.