Контакты

Случайная статья

Критерии оценивания

Стр 1 из 2Следующая ⇒

Задача 9. 3. Торможение шайбы. Шайбу толкнули по горизонтальной поверхности. Через время τ = 0, 1 с она оказалась на расстоянии S₁ = 8 см от начальной точки, а через 2τ – на расстоянии S₂ = 12 см. Найдите значения коэффициента трения μ между шайбой и поверхностью, при которых это возможно. Ускорение свободного падения g = 10 м/с².

Возможное решение. На шайбу после начального толчка действуют 3 силы: сила тяжести, сила нормальной реакции опоры и сила трения скольжения. В результате, до остановки шайба будет двигаться с ускорением

.

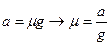Если к моменту 2τ шайба ещё не остановилась, то справедлива система уравнений:

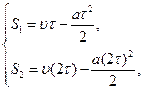(1)

где υ - начальная скорость шайбы.

Решая систему, получим:

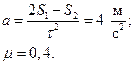
Если шайба остановилась между τ и2τ, то справедлива другая система уравнений:

(2)

Из данной системы получаем уравнение для a:

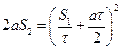. (3)

Решением данного уравнения будет соотношение: .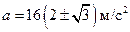

Корень с «+» при проверке даёт время остановки, меньшее, чем τ , что противоречит условию.

Корень с «–» даёт время остановки между τ и2τ , что и необходимо.

Этому ускорению соответствует коэффициент трения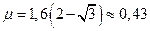

Критерии оценивания

1. Коэффициент трения выражен через ускорение 1 балл

2. Записана система уравнений [1] 1 балл

3. Найдено первое значение μ = 0, 4 2 балла

a) Получено выражение для a 1 балл

b) Получено выражение для μ или значение для a 0, 5 балла

c) Получено значение для μ 0, 5 балла

4. Указано, что возможен случай с остановкой до 2τ 1 балл

5. Записана система уравнений [2] 1 балл

6. Получено уравнение [3] 1, 5 балла

7. Найдены корни уравнения [3] 1 балл

8. Найдено второе значение 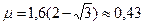1, 5 балла

a) Обоснованно выбрано одно из значений a 1 балл

b) Получено значение для μ 0, 5 балла

12 Следующая ⇒

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.