
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
КОРРЕЛЯЦИЯ И РЕГРЕССИЯ
Всем хорошо известна функциональная зависимость между числовыми множествами (рядами). Напомним её определение применительно к числовым рядам.
Между числовыми рядами Х и Y существует функциональная зависимость, если каждому значению величины Х ставится в соответствие единственное, строго определённое значение величины Y: y=f(x).
Функциональная зависимость может задаваться описательно, таблично, графически, аналитически.
Между тем, математический аппарат может быть использован для описания зависимостей, связанных между собой не только функционально, но и статистически, то есть, имеющих тенденцию зависимости, но без её строгой детерминации. Мы ограничимся здесь частным случаем статистической зависимости – корреляционной зависимостью.
Корреляционной называется зависимость между величинами Х и Y, если изменение одной величины влечёт за собой изменение математического ожидания другой величины.
Пример. Пары величин, связанные корреляционной зависимостью:
1. Масса и рост тела человека.
2. Количество внесённых удобрений и урожайность.
3. Верхнее и нижнее артериальное давление.
4. Влажность воздуха и атмосферное давление.
Естественно, что не каждая статистическая зависимость является корреляционной.
Корреляционную зависимость можно описать с помощью уравнения вида:
М(Yx)=f(x), которое называется уравнением регрессии Y на Х.
Здесь М(Yx) – условное математическое ожидание величины Y, соответствующее данному значению Х; х – отдельное значение величины Х; f(x) – некоторая функция, наиболее точно описывающая влияние значений ряда X на значения ряда Y. Уравнение регрессии показывает, на сколько будет изменяться математическое ожидание ряда Y при изменении значения варианты ряда X на единицу.
Обратную корреляционную зависимость можно описать уравнением регрессии Х на Y (существует не всегда): M(Хy)=j(y)
Графики функций регрессии f(x) и j(y) называются линиями регрессии. В зависимости от вида уравнения они могут быть линейными, степенными, показательными и так далее.
Если функции f(x) и j(y) линейны, то уравнения регрессии можно представить в виде: М(Yx)=Ax+B и М(Хy)=Сy+D
Линиями регрессии при этом являются прямые линии.
При достаточно большом числе значений величин Х и Y их математические ожидания можно заменить соответствующими средними арифметическими значениями: 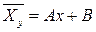 и
и 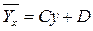
Наличие корреляционной зависимости между изучаемыми параметрами X и Y определяется вычислением коэффициента парной корреляции rxy:
 , где Cxy – корреляционный момент, а σ x, σ y – средние квадратические отклонения рядов X и Y.
, где Cxy – корреляционный момент, а σ x, σ y – средние квадратические отклонения рядов X и Y.
Основные свойства коэффициента корреляции:
1. Коэффициент корреляции двух независимых величин равен нулю (то есть, если rxy=0, то корреляционная зависимость между рядами X и Y отсутствует).
2. Коэффициент корреляции двух величин, связанных линейной функцией, равен ±1 («+», если прямая (возрастающая), а «-», если обратная (убывающая) зависимость).
3. Абсолютная величина коэффициента корреляции не превышает единицы: -1£ rxy£ 1
4. Корреляционную зависимость различают по величине коэффициента корреляции:
· rxy> 0 – корреляция прямая, то есть увеличение значений признака Х влечёт за собой увеличение значений признака Y;
· rxy< 0 – корреляция обратная;
· 0£ ½ rxy½ £ 0, 4 – слабая;
· 0, 4< ½ rxy½ £ 0, 7 – средняя;
· 0, 7< ½ rxy½ £ 1 – тесная.
На практике обычно имеют дело с ограниченным объёмом выборок изучаемых величин Х и Y, получаемых в результате независимых испытаний:
(х1; у1); (х2; у2); (х3; у3); …; (хn; yn).
1. Первым этапом статистической обработки результатов с целью определения наличия и вида корреляционной зависимости является составление корреляционной таблицы.
Корреляционная таблица содержит всю информацию, полученную в результате выборочных наблюдений величин Х и Y.
Для малых выборок (n< 30) одинакового объёма расчётная корреляционная таблица может иметь следующий вид:
| i | X | Y | X 2 | Y 2 | X∙ Y |
| x1 | y1 | 
| 
| x1∙ y1 | |
| x2 | y2 | 
| 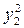
| x2∙ y2 | |
| … | … | … | … | … | … |
| i | xi | yi | 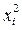
| 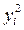
| xi∙ yi |
| … | … | … | … | … | … |
| n | xn | yn | 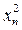
| 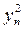
| xn∙ yn |
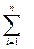 (по столбцам) (по столбцам)
| 
| 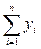
| 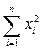
| 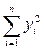
| 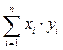
|
2. Далее, по исходной таблице вычисляем промежуточные величины (средние арифметические значения, средние квадратические отклонения случайных величин и их корреляционный момент), необходимые для исследования вида зависимости и нахождения функций регрессии.
· Средние арифметические: 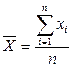 ;
; 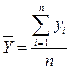 ;
;
· Дисперсии: 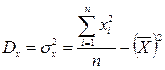 ;
; 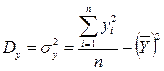 ;
;
· Выборочные средние квадратические отклонения: 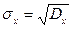 ;
; 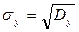 ;
;
· Корреляционный момент (коэффициент ковариации):
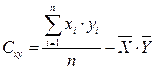
3. Проверяя гипотезу существования связи между рядами Х и Y, определяем значение выборочного коэффициента линейной корреляции:

4. По знаку и величине коэффициента корреляции оцениваем наличие, тесноту и характер корреляционной связи.
5. Для оценки достоверности коэффициента корреляции определяют его погрешность: 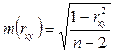 и вычисляют экспериментальное значение коэффициента Стьюдента:
и вычисляют экспериментальное значение коэффициента Стьюдента:
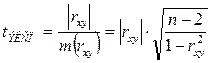
Для того, чтобы убедиться, что коэффициент корреляции, вычисленный по данным выборочного исследования, будет соответствовать размеру связи в генеральной совокупности, необходимо определить по таблице критических значений Стьюдента (табл. 1) значение критерия tКРИТ для числа степеней свободы f=n-2 и выбранной доверительной вероятности (выбранного уровня значимости α ).
Тогда:
· если tЭКСП³ tКРИТ, то при принятой вероятности делают вывод о значимости коэффициента корреляции;
· если tЭКСП< tКРИТ, то такой вывод сделать нельзя.
Найденный коэффициент корреляции указывает лишь на направление и тесноту связи между двумя переменными величинами, но не даёт возможности судить о том, как количественно меняются величины одного признака по мере изменения величины другого признака. Ответ на этот вопрос даёт применение метода регрессии.
Регрессия – это функция, позволяющая по величине одного коррелирующего признака определить средние величины другого признака.
С помощью регрессии решается задача: как количественно меняется одна величина при изменении другой величины на единицу.
Функция регрессии может иметь любой вид (линейная, степенная, показательная) и методы регрессионного анализа позволяют отыскать внешний вид этой функции.
Подробнее познакомимся с линейной регрессией.
Между коэффициентом корреляции rxy, числовыми характеристиками выборок и коэффициентами уравнения линейной регрессии существует определённая связь.
Для уравнения: 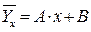 :
:  и
и 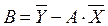
Для уравнения: 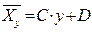 :
: 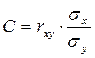 и
и 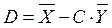
Имея частные решения уравнений линейной регрессии, можно построить их графики: (рис. 1).
Линии регрессии пересекаются в точке 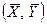 , при этом tga=A.
, при этом tga=A.
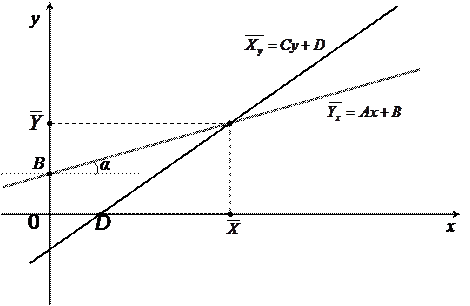 |
Рис. 1.
 |
Ориентировочно о силе корреляционной зависимости можно судить по корреляционному полю (рис. 2).
Рис. 2.
Корреляционное поле представляет собой множество точек с координатами (хi; yi):
Чем больше разброс точек (рис. 2а), тем слабее зависимость, и наоборот, если точки группируются вдоль некоторой линии (рис. 2б), то зависимость тесная и можно приближённо судить не только о силе, но и даже о виде функции регрессии.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|