
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Исследование непрерывности функции в
Исследование непрерывности функции в
заданных точках “ 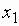 ” и “
” и “ 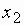 ”
”
Функция 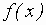 считается непрерывной в точке
считается непрерывной в точке 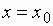 , если пределы слева и справа существуют и равны значению
, если пределы слева и справа существуют и равны значению 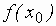 .
.
Пример
Дана функция 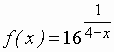 ,
,
исследовать на непрерывность в точках 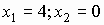 , сделать схематический чертеж.
, сделать схематический чертеж.
Решение:
Находим левосторонние и правосторонние пределы при 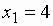 :
:
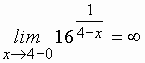 (левосторонний предел при
(левосторонний предел при 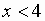 , т. е. знаменатель показателя степени
, т. е. знаменатель показателя степени 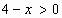 и стремится к нулю, в этом случае
и стремится к нулю, в этом случае
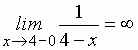 ,
,
следовательно, и 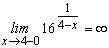 .
.
Правосторонний предел:
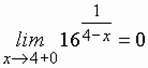 (правосторонний предел при
(правосторонний предел при 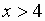 и
и 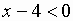 , т. е. показатель степени отрицательный, и выражение под знаком предела можно переписать в виде
, т. е. показатель степени отрицательный, и выражение под знаком предела можно переписать в виде
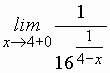 ,
,
где знаменатель стремится к бесконечности).
Таким образом, функция
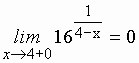
имеет разрыв в точке 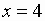 .
.
Рассмотрим эту функцию в окрестности 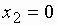 . В этом случае левосторонний и правосторонний пределы равны:
. В этом случае левосторонний и правосторонний пределы равны:
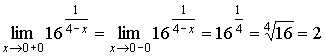 ,
,
следовательно, в точке 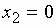 , функция непрерывна.
, функция непрерывна.
Схематический чертеж (рисунок):
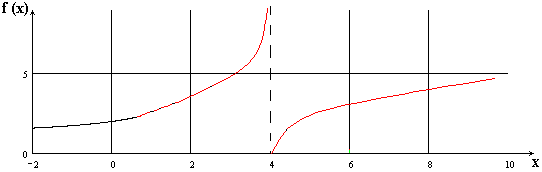
Рисунок
Теоретические вопросы к разделу 2
1. Условия непрерывности функции в точке. Левосторонние и правосторонние пределы.
2. Классификация точек разрыва.
Задание 1 к разделу 2. Задана функция y = f(x) и два значения аргумента х1 и х2.
Требуется установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента, и сделать схематический чертеж.
| 1. f(x)=91/(2-x), | x1 = 0, | x2 = 2. |
| 2. f(x)=41/(3-x), | x1 = 1, | x2 = 3. |
| 3. f(x)=121/x, | x1 = 0, | x2 = 2. |
| 4. f(x)=31/(4-x), | x1 = 2, | x2 = 4. |
| 5. f(x)=81/(5-x), | x1 = 3, | x2 = 5. |
| 6. f(x)=101/(7-x), | x1 = 5, | x2 = 7. |
| 7. f(x)=141/(6-x), | x1 = 4, | x2 = 6. |
| 8. f(x)=151/(8-x), | x1 = 6, | x2 = 8. |
| 9. f(x)=111/(4+x), | x1 = -4, | x2 = -2. |
| 10. f(x)=131/(5+x), | x1 = -5, | x2 = -3. |
| 11. f(x)=91/(2-x), | x1 = 0, | x2 = 2. |
| 12. f(x)=41/(3-x), | x1 = 1, | x2 = 3. |
| 13. f(x)=121/x, | x1 = 0, | x2 = 2. |
| 14. f(x)=31/(4-x), | x1 = 2, | x2 = 4. |
| 15. f(x)=81/(5-x), | x1 = 3, | x2 = 5. |
| 16. f(x)=101/(7-x), | x1 = 5, | x2 = 7. |
| 17. f(x)=141/(6-x), | x1 = 4, | x2 = 6. |
| 18. f(x)=151/(8-x), | x1 = 6, | x2 = 8. |
| 19. f(x)=111/(4+x), | x1 = -4, | x2 = -2. |
| 20. f(x)=131/(5+x), | x1 = -5, | x2 = -3. |
| 21. f(x)=91/(2-x), | x1 = 0, | x2 = 2. |
| 22. f(x)=41/(3-x), | x1 = 1, | x2 = 3. |
| 23. f(x)=121/x, | x1 = 0, | x2 = 2. |
| 24. f(x)=31/(4-x), | x1 = 2, | x2 = 4. |
| 25. f(x)=81/(5-x), | x1 = 3, | x2 = 5. |
| 26. f(x)=101/(7-x), | x1 = 5, | x2 = 7. |
| 27. f(x)=141/(6-x), | x1 = 4, | x2 = 6. |
| 28. f(x)=151/(8-x), | x1 = 6, | x2 = 8. |
| 29. f(x)=111/(4+x), | x1 = -4, | x2 = -2. |
| 30. f(x)=131/(5+x), | x1 = -5, | x2 = -3. |
Задание 2 к разделу 2. Задана функция y = f(x). Найти точки разрыва функции, если они существуют. Сделать чертеж.
1. 
| 6. 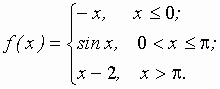
|
2. 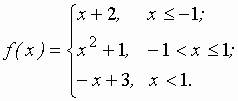
| 7. 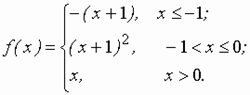
|
3. 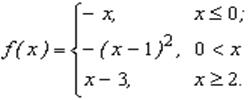
| 8. 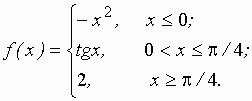
|
4. 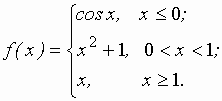
| 9. 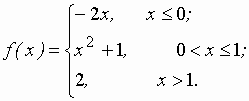
|
5. 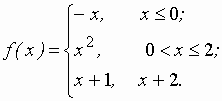
| 10. 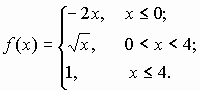
|
11. 
| 16. 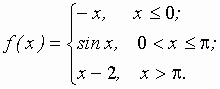
|
12. 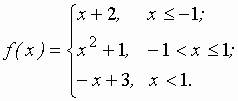
| 17. 
|
13. 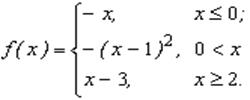
| 18. 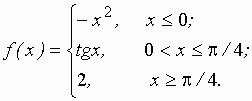
|
14. 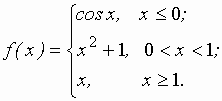
| 19. 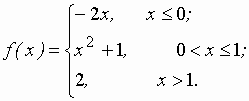
|
15. 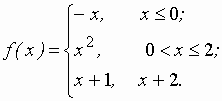
| 20. 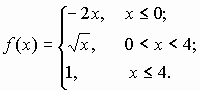
|
21. 
| 26. 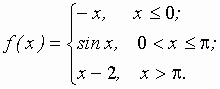
|
22. 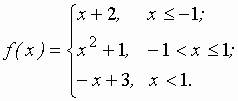
| 27. 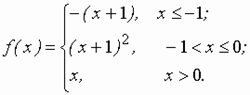
|
23. 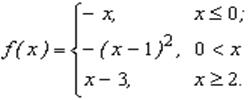
| 28. 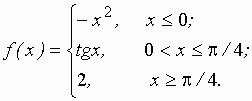
|
24. 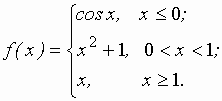
| 29. 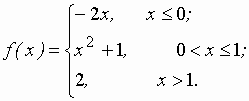
|
25. 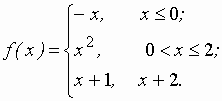
| 30. 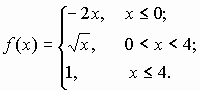
|
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|