
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Ход урока. Cmn =m!/(m-n)!n!
Группа: ПС 1-13
Дата: 01. 02. 22 (4 пара)
Дисциплина: Математика
Тема урока: Сочетания
Преподаватель: Старцева М. С.
Тип урока: Изучение нового материала.
Цель урока:
Цель
Сформировать знания о комбинаторных соединениях. Научить применять новые знания на практике; выработать и закрепить навыки определения вида комбинаторного соединения и нахождения их числа (решения задач).
Ход урока
Организационный момент
Подготовка тетради, учебника к уроку
Написать в тетрадях тему урока и дату
Изложение нового материал
Сочетаниями из m элементов по n в каждом(n≤ т) называются такие соединения, каждое из которых содержит n элементов, взятых из данных m элементов, и которые отличаются одно от другого, по крайней мере, одним элементом.
Число сочетаний обозначается Cmn(читается " це из эм по эн" ) Буква C выбрана для обозначения числа сочетаний в связи тем, что по-французски слово " сочетание" - " combinaison" - начинается с этой буквы.
Формула для подсчета числа сочетаний из m различных элементов по n элементов в каждом:
Cmn =m! /(m-n)! n!
Например, рассмотрим учебную группу, состоящую из 25 человек. Построение всевозможных списков из имеющегося числа фамилий всех студентов этой учебной группы – перестановки. Число таких списков равно числу перестановок из 25 фамилий и вычисляется Р25 = 25! Если из учебной группы нужно отобрать трех человек, то есть из общего числа 25 выбрать 3, то это комбинация – сочетания из 25 по 3. Количество таких списков по 3 фамилии из 25 будет равно числу сочетаний из 25 по 3 и вычисляться по формуле C 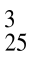 =
= 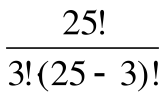 =
= 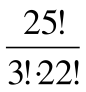 =
= 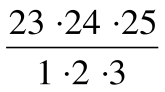 = 2300. Если из учебной группы нужно отобрать трех человек с присвоением каждому определенного номера, то есть из общего числа 25 выбрать 3 и расставить в определенном порядке, то это комбинация – размещения из 25 по 3. Количество таких списков будет равно числу размещений из 25 по 3 и вычисляться по формуле А
= 2300. Если из учебной группы нужно отобрать трех человек с присвоением каждому определенного номера, то есть из общего числа 25 выбрать 3 и расставить в определенном порядке, то это комбинация – размещения из 25 по 3. Количество таких списков будет равно числу размещений из 25 по 3 и вычисляться по формуле А 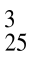 =
= 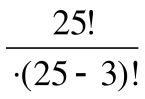 = =
= = 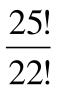 = 23∙ 24∙ 25= 13800.
= 23∙ 24∙ 25= 13800.
Пример: Решим следующую задачу. Пусть в коробке находится пять пронумерованных шаров {1, 2, 3, 4, 5}. Перечислите все способы выбора двух шаров из этих пяти.
Каждому способу выбора двух шаров из пяти соответствует некоторое двухэлементное подмножество пятиэлементного множества. Перечислим эти подмножества:

Обратите внимание, что подмножества (2, 1) и (1, 2) содержат один и тот же набор элементов и поэтому отождествляются. Итак, у пятиэлементного множества 10 двухэлементных подмножеств.
C52 = 10
Число сочетаний, перестановок и размещений связано формулой:
Amn=Cmn · Pn
Задача: Сколько рукопожатий получится, если здороваются 5 человек?
{Вася, Петя}={Петя, Вася}–одно и тоже.
Значит, порядок неважен, значит это подмножество по два элемента из 5,
значит это сочетание из пяти по два.
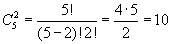
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|