Хелпикс

Главная

Контакты

Случайная статья



Степень с действительным показателем



Степень с действительным показателем

 

Определение 1. Действительные числа - это рациональные и иррациональные числа. Множество действительных чисел обозначается через R.

Или можно дать другое определение:

Определение 2. Действительные числа - числа, которые можно записать в виде конечной или бесконечной (периодической или непериодической) десятичной дроби.

Действительные числа - это любые рациональные и иррациональные числа. Приведем примеры таких чисел: 0; 6; 458; 1863; 0, 578; − 3 8; 5 √ 26; 0, 145 ( 3 ).

Нуль также является действительным числом. Согласно определению, существуют как положительные, так и отрицательные действительные числа. Нуль является единственным действительным числом, которое не положительно и не отрицательно. Еще одно название для действительных чисел - вещественные числа. Эти числа позволяют описывать значение непрерывно меняющейся величины без введения эталонного (единичного) значения этой величины.

Определение 3. Пусть дано положительное число a и произвольное действительное число x. Число 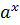 называется степенью, число a - основанием степени, число x - показателем степени.

По определению полагают:

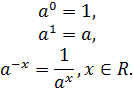
Если a и b - положительные числа, x и y - любые действительные числа, то справедливы следующие свойства.

 

Свойства степени с действительным показателем

1) ,

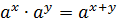2) ,

3) ,

4) ,

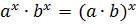5) ,

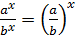6)

 

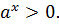
Пример 1. Упростить числовые и алгебраические выражения:

1.

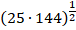
2.

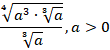
Решение.

1. .

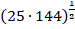Представляем 25 и 144 в виде степеней:

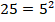
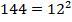
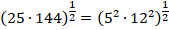
Теперь используем свойства степеней:

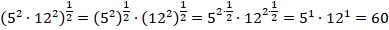
2.

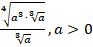
Поскольку основание степени больше нуля, можем перейти к степеням:

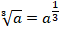
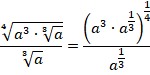
Используем свойства степеней:

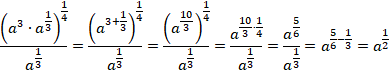
Или, если перейти к корням, или просто .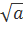

 

Задачи для самостоятельного решения (домашняя работа)



  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.