Семинар по теме «Фазовое равновесие в однокомпонентных системах» № 2

1. Определить температуру кипения хлорбензола при 26, 66 кПа (200 мм рт. ст. ), если его нормальная температура кипения 405, 4 К, а при 53, 33 кПа (400 мм рт. ст. ) он кипит при температуре 383, 2 К. Вычислить теплоту испарения, изменение энтропии, внутренней энергии, энергии Гиббса и энергии Гельмгольца при испарении 1 моль хлорбензола при нормальной температуре кипения.

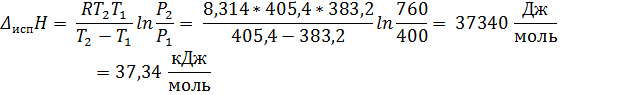
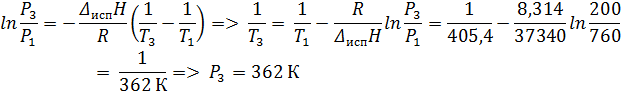
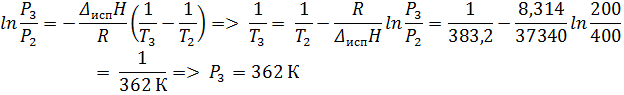
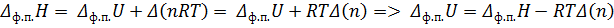
, где 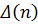изменение количества газообразных веществ, в случае испарения:

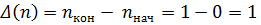
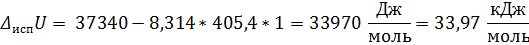
Для любого равновесного фазового перехода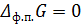

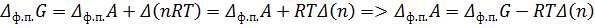
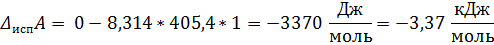
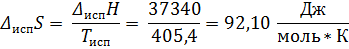
Ответ: Т = 362 К; ∆ Н_исп = 37, 34 кДж/моль; ∆ S_исп = 92, 10 Дж/(моль * К); ∆ U_исп = 33, 97 кДж/моль; ∆ G_исп = 0 кДж/моль; ∆ А_исп = -3, 37 кДж/моль.

2. Зависимость давления (Па) насыщенного пара от температуры для фреона CCl₂F₂ выражается уравнением lgP = 34, 5 – 2406, 1/T – 9, 26lgT + 0, 0037T. Определить давление насыщенного пара, теплоту испарения, изменение энтропии, энергии Гиббса и теплоёмкости при испарении 1 моля фреона при 298 К.

Подставив в исходное уравнение температуру рассчитаем давление насыщенного пара над фреоном:

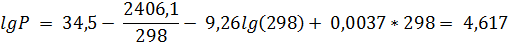
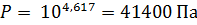
Для расчёта остальных функций переведём логарифм в натуральный:

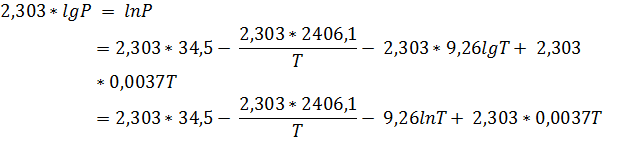
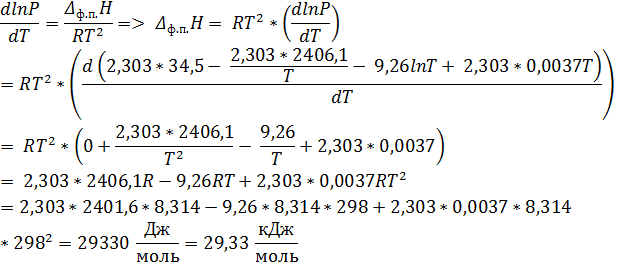
По закону Кирхгоффа:

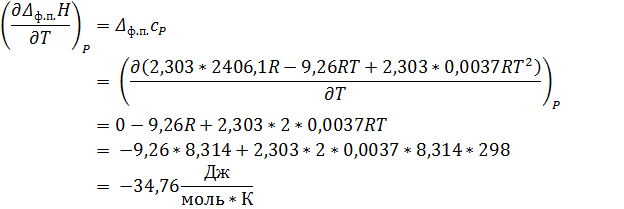
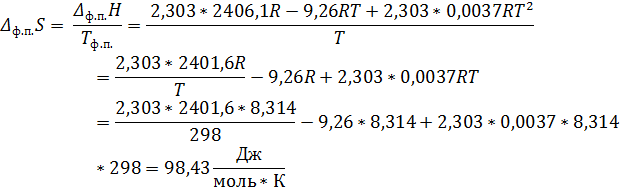
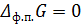
Ответ: P = 4, 14 * 10⁴ Па; ∆ Н_исп = 29, 33 кДж/моль; ∆ S_исп = 98, 43 Дж/моль К; ∆ G_исп = 0 кДж/моль; ∆ С_P = -34, 76 Дж/моль К.

3. На основании справочных данных о значениях температуры кипения при различном внешнем давлении рассчитайте температурный коэффициент давления насыщенного пара (dP/dT) для метилового спирта при нормальной температуре кипения. Теплоту испарения метанола в интервале 45 – 65 º С принять постоянной величиной.

Для самостоятельного решения.

Ответ: P₁ = 400 мм рт. ст.; Т₁ = 49, 9 º С; P₂ = 760 мм рт. ст.; Т₂ = 64, 5 º С (стр. 30 спр. Равделя); ∆ Н_исп = 39, 87 кДж/моль; dP/dT = 4261 Па/К.

4. При 1, 01 * 10⁵ Па и -38, 87 º С жидкая ртуть имеет плотность 13, 69 г/см³, а твёрдая 14, 19 г/см³. Рассчитайте температуру плавления ртути при давлении 3 * 10⁸ Па, если удельная теплота плавления ртути равна 9, 74 Дж/г.

Запишем уравнение Клаузиуса:

Разделим переменные:

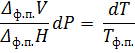
Необходимо выразить разницу между объёмами твёрдой и жидкой фаз через имеющиеся плотности ртути:

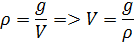
, где 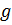масса вещества

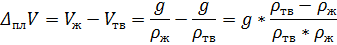
Если в качестве массы взять величину равную молярной массе, то получится молярное изменение объёма, если 1 кг – то изменение объёма при плавлении 1 килограмма ртути. Поскольку теплота плавления дана в Дж/г, в качестве массы удобнее брать 1 кг и все используемые величины переводить в систему СИ. Тогда:

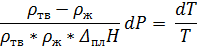
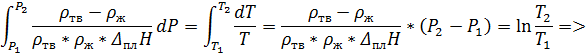
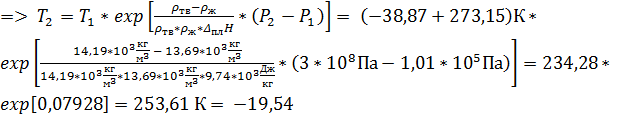º С

Ответ: 253, 61 К.

5. Зависимость температуры плавления калия от давления (атм), по Бриджмену, выражается уравнением

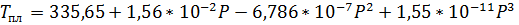Определите температуру плавления и теплоту плавления при давлениях 1, 6 атм и 12000 атм, если изменение объёма 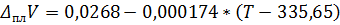, см³/г.

Рассчитаем температуры плавления:

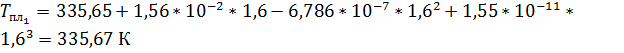
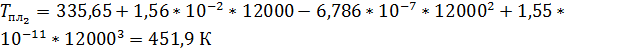
Запишем уравнение Клаузиуса:

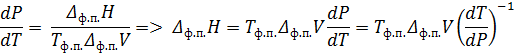
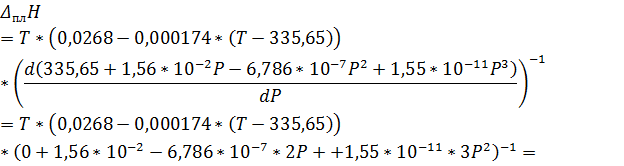
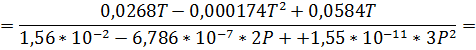
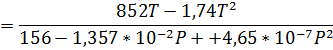
Обратите внимание, что знаменатель был получен из уравнения зависимости температуры от давления, выраженного в атмосферах. Т. е. приведённые коэффициенты имеют смысл, только при подстановке давления в атмосферах. Числитель же содержал зависимость объёма от температуры выраженную в см³/г. Таким образом, рассчитывая теплоту плавления по уравнению выше ответ будет получаться в .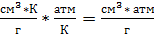

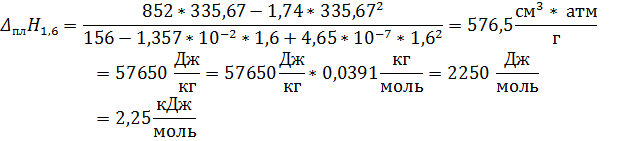
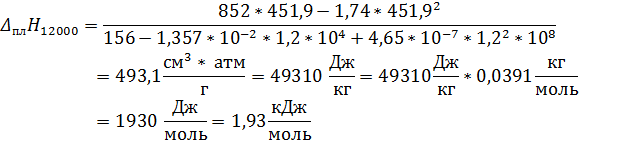
Ответ: Т_пл1 = 335, 67 К; Т_пл2 = 451, 9 К; Δ _плH₁ = 2, 25 кДж/моль; Δ _плH₂ = 1, 93 кДж/моль.

12 Следующая ⇒