Распределение Больцмана

Распределение Больцмана определяет распределение частиц в силовом поле в условиях теплового равновесия.

Пусть идеальный газ находится в поле консервативных сил в условиях теплового равновесия. При этом концентрация газа будет различной в точках с различной потенциальной энергией, что необходимо для соблюдения условий механического равновесия. Так, число молекул в единичном объеме n убывает с удалением от поверхности Земли, и давление, в силу соотношения P = nkT, падает.

Если известно число молекул в единичном объеме, то известно и давление, и наоборот. Давление и плотность пропорциональны друг другу, поскольку температура в нашем случае постоянна. Давление с уменьшением высоты должно возрастать, потому что нижнему слою приходится выдерживать вес всех расположенных сверху атомов.

Исходя из основного уравнения молекулярно-кинетической теории: P = nkT, заменим P и P₀ в барометрической формуле (2. 4. 1) на n и n₀ и получим распределение Больцмана для молярной массы газа:

рис. 1

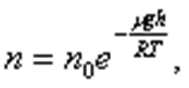
где n₀ и n - число молекул в единичном объёме на высоте h = 0 и h.

Так как 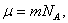а 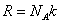, то рис. 1 можно представить в виде

рис. 2

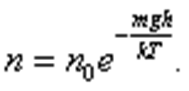
С уменьшением температуры число молекул на высотах, отличных от нуля, убывает. При T = 0 тепловое движение прекращается, все молекулы расположились бы на земной поверхности. При высоких температурах, наоборот, молекулы оказываются распределёнными по высоте почти равномерно, а плотность молекул медленно убывает с высотой. Так как mgh – это потенциальная энергия U, то на разных высотах U = mgh – различна. Следовательно, рис. 2 характеризует распределение частиц по значениям потенциальной энергии:

рис. 3

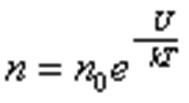– это закон распределения частиц по потенциальным энергиям – распределение Больцмана. Здесь n₀ – число молекул в единице объёма там, где U = 0.

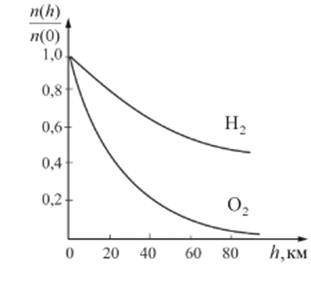
На рис. 4 показана зависимость концентрации различных газов от высоты. Видно, что число более тяжелых молекул с высотой убывает быстрее, чем легких.

рис. 4

Из рис. 3 можно получить, что отношение концентраций молекул в точках с U₁ и i > U₂ равно:

рис. 5

Больцман доказал, что соотношение (рис. 3) справедливо не только в потенциальном поле сил гравитации, но и в любом потенциальном поле, для совокупности любых одинаковых частиц, находящихся в состоянии хаотического теплового движения.