
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тульский государственный университет
Тульский государственный университет
Кафедра " Автоматизированные станочные системы"
ТЕОРИЯ ВЕРОЯТНОСТЕЙ, МАТЕМАТИЧЕСКАЯ СТАТИСТИКА И СЛУЧАЙНЫЕ ПРЦЕССЫ
Контрольная работа.
Оценка параметров функции распределения и построение гистограммы по опытным данным
Студент гр. 220901 Селищева Н. О ___________
Преподаватель проф. каф. АСС Пасько Н. И. ___________
Тула - 2012
1. Построение вариационного ряда
Построим вариационный ряд, расположив все числа выборки в порядке возрастания. Полученный вариационный ряд представлен ниже.
0. 26 0. 80 0. 90 0. 95 1. 31 1. 42 1. 48 1. 58
1. 59 1. 65 1. 67 1. 97 2. 09 2. 20 2. 34 2. 41
2. 44 2. 52 2. 55 2. 60 2. 68 2. 76 2. 80 2. 99
3. 07 3. 12 3. 12 3. 18 3. 24 3. 30 3. 31 3. 31
3. 39 3. 65 3. 65 3. 76 3. 78 3. 81 3. 86 3. 98
4. 13 4. 29 4. 39 4. 46 4. 50 4. 77 4. 78 4. 88
4. 93 5. 07 5. 07 5. 08 5. 12 5. 13 5. 15 5. 16
5. 29 5. 30 5. 41 5. 43 5. 51 5. 60 5. 66 5. 69
5. 72 5. 87 5. 90 5. 92 5. 94 6. 00 6. 18 6. 23
6. 42 6. 70 6. 76 6. 79 6. 80 6. 84 6. 89 6. 94
7. 04 7. 11 7. 34 7. 43 7. 45 7. 53 7. 56 7. 79
7. 91 8. 15 8. 41 8. 42 8. 54 8. 56 8. 86 8. 87
8. 99 9. 11 9. 33 9. 55
2. Нахождение Xmin и Xmax
X min = 0, 26
X max = 9, 55
3. Нахождение размаха
R = X max – X min = 9, 55-0, 26=9, 29;
4. Нахождение медианы
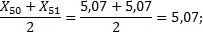
5. Нахождение среднего арифметического (математического ожидания)
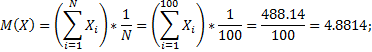
6. Нахождение статической дисперсии
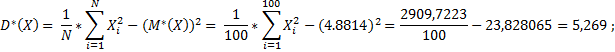
7. Нахождение квадратичного отклонения
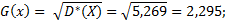
8. Построение функции распределения
Функцию распределения построим по формуле: 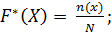 где n(x) – число точек вариационного ряда меньших X. График изображен на рис. 1.
где n(x) – число точек вариационного ряда меньших X. График изображен на рис. 1. 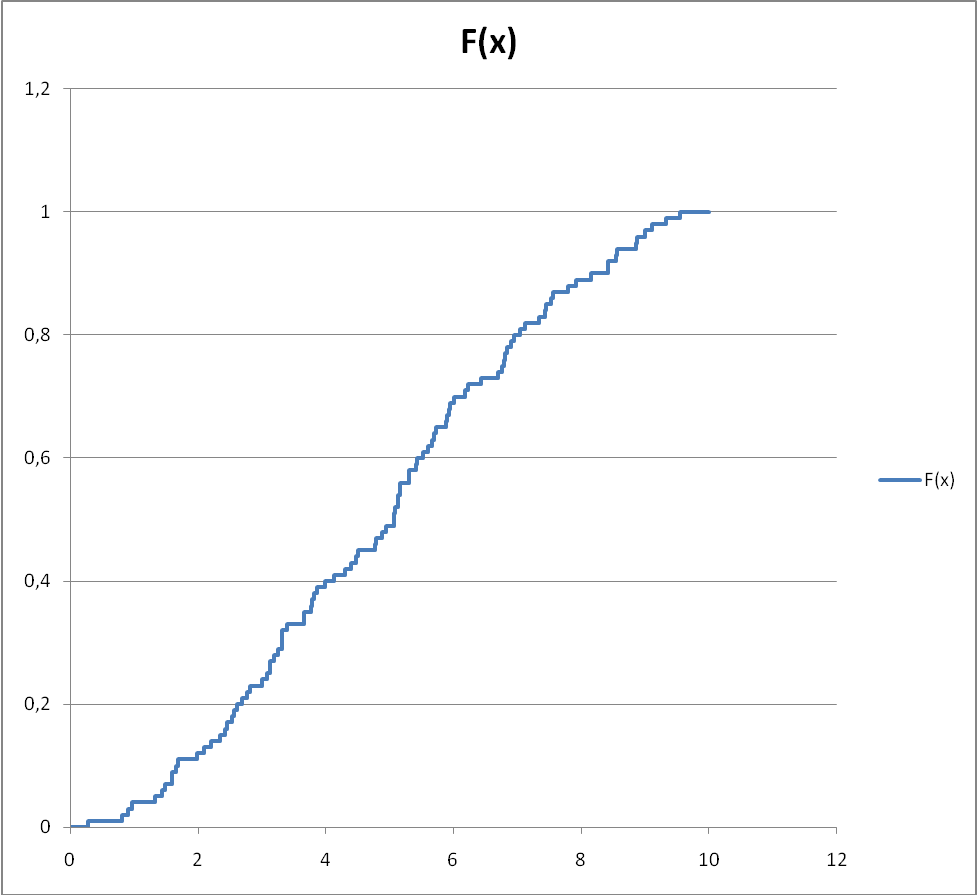
Рисунок 1 – График функции распределения.
9. Построение гистограммы
Построим следующую таблицу, для построения гистограммы.
| Номер интервала | ||||||||||
| Интервал | 0-1 | 1-2 | 2-3 | 3-4 | 4-5 | 5-6 | 6-7 | 7-8 | 8-9 | 9-10 |
| Nj* | ||||||||||
| Pj* | 0. 04 | 0. 08 | 0. 12 | 0. 16 | 0. 09 | 0. 2 | 0. 11 | 0. 09 | 0. 08 | 0. 03 |
| fj* | 0. 04 | 0. 08 | 0. 12 | 0. 16 | 0. 09 | 0. 2 | 0. 11 | 0. 09 | 0. 08 | 0. 03 |
Для построения таблицы использовались следующие формулы:
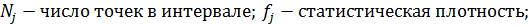
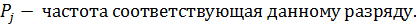
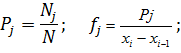
Построенная гистограмма изображена на рис. 2.
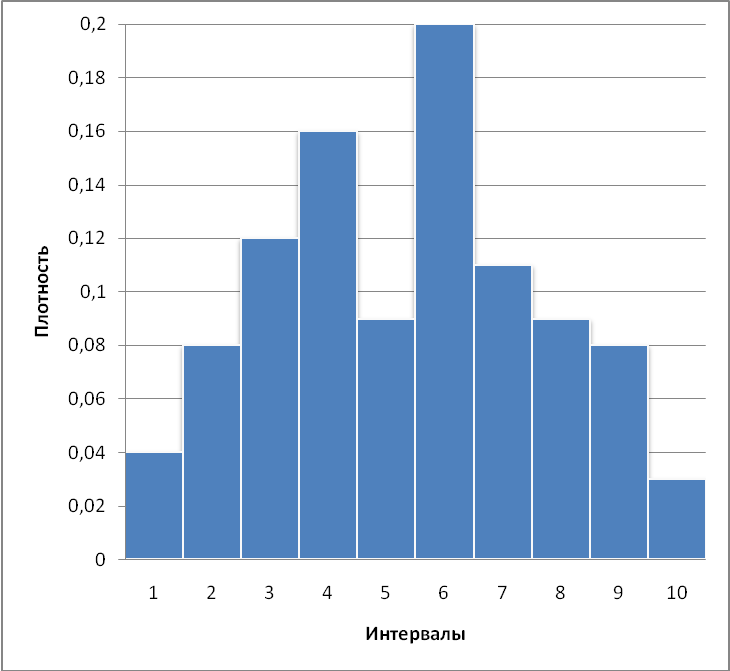
Рисунок 2 – Гистограмма статистического распределения.
Из гистограммы определяем статистическую моду 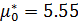 .
.
10. Оценка параметров распределения.
а) метод моментов
Исходное распределение имеет два параметра 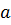 и
и 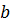 , поэтому для их оценки имеем два уравнения, полученные приравниванием математических ожиданий и дисперсий:
, поэтому для их оценки имеем два уравнения, полученные приравниванием математических ожиданий и дисперсий:
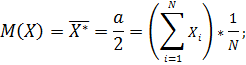
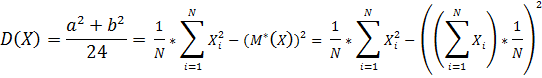
Найдем параметр 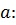
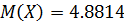 (см. 5 пункт), то
(см. 5 пункт), то 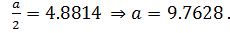
Найдем параметр 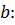
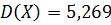 (см. 6 пункт), то
(см. 6 пункт), то 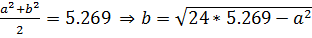 .
.
Так как 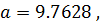
то 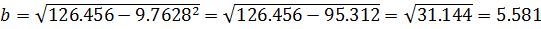 .
.
б) метод наибольшего правдоподобия
Так как функция распределения имеет непрерывную плотность распределения:
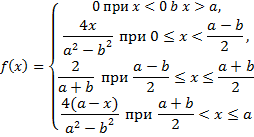
В этом случае функция правдоподобия имеет вид:
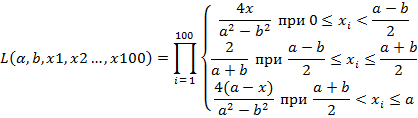
Максимум этой функции достигается если 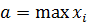 ,
,
то есть в качестве оценки для 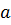 следует брать наибольшее значение из выборки.
следует брать наибольшее значение из выборки.
Найдем параметр 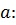
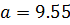 .
.
Найдем параметр 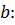
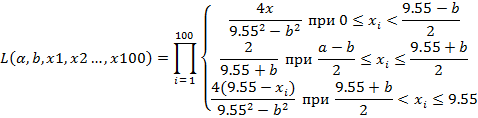
Решая данное уравнение с помощью пакета Wolfram Mathematica 8. 0, получаем значение параметра 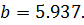
Найденные значения 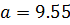 и
и 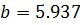 совпали с найденными значениями по методу моментов. Следовательно, данные параметры найдены правильно.
совпали с найденными значениями по методу моментов. Следовательно, данные параметры найдены правильно.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|