- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное автономное образовательное учреждение
высшего образования
«Севастопольский государственный университет»
Кафедра «Информационные системы»
Контрольная работа
По дисциплине: «ТЕОРИЯ ВЕРОЯТНОСТЕЙ ВЕРОЯТНОСТНЫЕ ПРОЦЕССЫ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА»
Вариант № 2
Выполнил:
Студент курса
Заочного отделения
Группа №
Сербин Александр Александрович
Проверил:
Преподаватель
Профессор Доценко Станислав Васильевич
Севастополь
задание для выполнения Комплексной контрольной работы
по дисциплине «Теория вероятностей вероятностные процессы и математическая статистика»
Вариант № 2
1. Тестовые вопросы
| Номер вопроса | Номер вопроса из общего списка |
2. Комплексное задание
Вариант 2.
|
1. Тестовые вопросы:
1. (2) Случайное явление — это такое явление, которое:
1) можно точно предсказать;
2) при каждом испытании дает один и тот же результат;
3) для выяснения его закономерностей достаточно провести небольшое количество опытов;
4) при многократном проведении одного и того же опыта протекает каждый раз несколько по-иному, причем эти отличия заранее точно не предсказуемы.
Ответ: 4.
2. (8) Вероятности 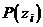 исходов эксперимента
исходов эксперимента 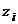 представляют собой:
представляют собой:
1) целые числа;
2) рациональные числа;
3) вещественные числа, лежащие в диапазоне 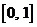 ;
;
4) комплексные числа.
Ответ: 3.
3. (10) Имеются два случайных исхода 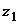 и
и 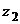 эксперимента с вероятностями
эксперимента с вероятностями 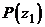 и
и 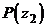 . Какое из соотношений верно:
. Какое из соотношений верно:
1) 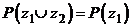 ; 2)
; 2) 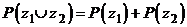 ;
;
3) 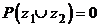 ; 4)
; 4) 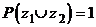 .
.
Ответ: 2.
4. (14) Какая из следующих формул описывает свойство дистрибутивности случайных событий 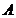 ,
, 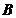 и
и 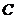 :
:
1) 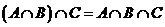 ; 2)
; 2) 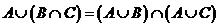 ;
;
3) 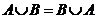 ; 4)
; 4) 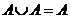 .
.
Ответ: 2.
5. (16)Укажите в приведенных формулах закон де Моргана:
1) 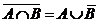 ; 2)
; 2) 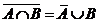 ; 3)
; 3) 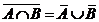 ; 4)
; 4) 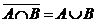 .
.
Ответ: 3.
6. (22) Случайные события 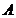 и
и 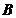 находятся в отношении
находятся в отношении 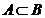 . Укажите правильное значение формулы для вероятности
. Укажите правильное значение формулы для вероятности 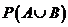 :
:
1) 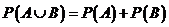 ; 2)
; 2) 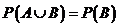 ;
;
3) 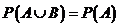 ; 4)
; 4) 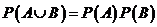 .
.
Ответ: 2.
7. (25) 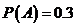 и
и 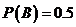 — вероятности случайных событий
— вероятности случайных событий 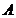 и
и 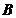 . Известно, что условная вероятность события
. Известно, что условная вероятность события 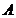 при условии, что
при условии, что 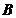 произошло, есть
произошло, есть 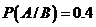 . Чему равна вероятность
. Чему равна вероятность 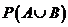 :
:
1) 0. 5; 2) 0. 6; 3) 0. 7; 4) 0. 8.
Ответ: 2.
8. (33)
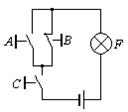
| Кнопки 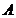 , , 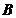 и и 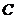 нажимаются случайно независимо друг от друга с вероятностями нажимаются случайно независимо друг от друга с вероятностями 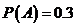 , , 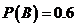 и и 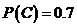 . Какова вероятность горения лампочки F:
1) 0. 215; 2) 0. 302; 3) 0. 406; 4) 0. 512? . Какова вероятность горения лампочки F:
1) 0. 215; 2) 0. 302; 3) 0. 406; 4) 0. 512?
|
Ответ: 4.
9. (36) Случайные величины могут быть получены:
1) в результате сложения неслучайных величин;
2) в результате измерения характеристик природных явлений;
3) при аналитическом решении дифференциальных уравнений;
4) при умножении неслучайных величин.
Ответ: 2.
10. (42) Какая характеристика является законом распределения дискретной случайной величины:
1) математическое ожидание;
2) дисперсия;
3) медиана;
4) интегральная функция распределения?
Ответ: 4.
11. (45) Какое из указанных свойств имеет интегральная функция распределения 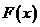 :
:
1) 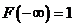 ; 2)
; 2) 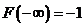 ; 3)
; 3) 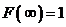 ; 4)
; 4) 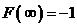 ?
?
Ответ: 3.
12. (47) Какие числовые характеристики случайных величин не являются
характеристиками положения:
1) математическое ожидание;
2) среднеквадратическое отклонение;
3) мода;
4) медиана?
Ответ: 2.
13. (51) Плотность вероятности непрерывной случайной величины 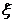 есть
есть 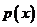 . Что представляет собой ее числовая характеристика
. Что представляет собой ее числовая характеристика 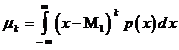 :
:
1) начальный момент порядка 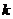 ;
;
2) дисперсия;
3) центральный момент порядка 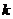 ;
;
4) математическое ожидание величины 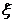 ?
?
Ответ: 3.
14. (55) Какая числовая характеристика пары непрерывных случайных величин 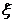 и
и 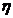 вычисляется с помощью выражения
вычисляется с помощью выражения 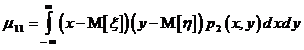 :
:
1) математические ожидания величин 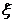 и
и 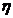 ;
;
2) дисперсии величин 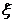 и
и 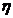 ;
;
3) корреляционный момент величин 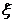 и
и 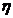 ;
;
4) коэффициенты асимметрии величин 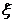 и
и 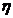 ?
?
Ответ: 3.
15. (58)Для двух дискретных случайных величин x и h заданы множества их возможных значений 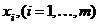 и
и 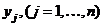 и совместные двумерные распределения вероятностей
и совместные двумерные распределения вероятностей

Какие множества чисел из указанных ниже являются одномерными распределениями вероятностей 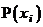 и
и 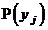 случайных величин x и h:
случайных величин x и h:
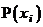
1) 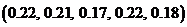 ; 2)
; 2) 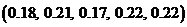 ;
;
3) 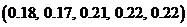 ; 4)
; 4) 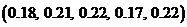 ;
;
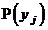
1) 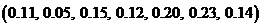 ; 3)
; 3) 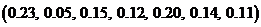 ;
;
2) 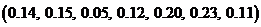 ; 4)
; 4) 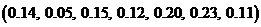 ?
?
Ответ: 2, 4.
16. (60) Для двух дискретных случайных величин x и h заданы множества их возможных значений 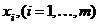 и
и 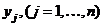 и совместные двумерные распределения вероятностей
и совместные двумерные распределения вероятностей
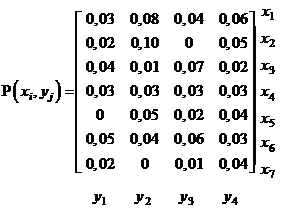
Какие множества чисел из указанных ниже являются одномерными распределениями вероятностей 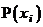 и
и 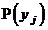 случайных величин x и h:
случайных величин x и h:
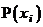
1) 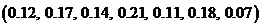 ;
;
2) 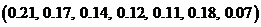 ;
;
3) 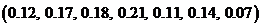 ;
;
4) 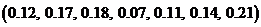 ;
;
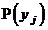
1) 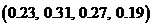 ; 2)
; 2) 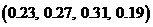 ;
;
3) 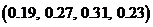 ; 4)
; 4) 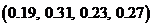 ?
?
Ответ: 2, 4.
17. (63) Для двух дискретных случайных величин x и h заданы множества их возможных значений 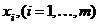 и
и 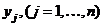 и совместные двумерные распределения вероятностей
и совместные двумерные распределения вероятностей

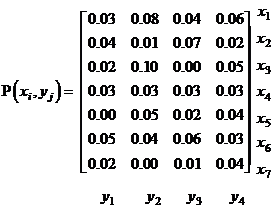
Какие множества чисел из указанных ниже являются одномерными распределениями вероятностей 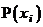 и
и 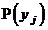 случайных величин x и h:
случайных величин x и h:
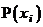
1) 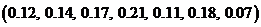 ; 3)
; 3) 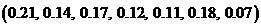 ;
;
2) 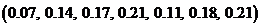 ; 4)
; 4) 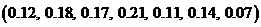 ;
;
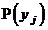
1) 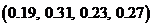 ; 2)
; 2) 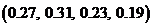 ;
;
3) 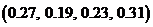 ; 4)
; 4) 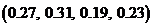 ?
?
Ответ: 3, 1.
18. (66) Для двух дискретных случайных величин x и h заданы множества их возможных значений 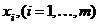 и
и 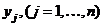 и совместные двумерные распределения вероятностей
и совместные двумерные распределения вероятностей


Какие множества чисел из указанных ниже являются одномерными распределениями вероятностей 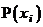 и
и 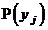 случайных величин x и h:
случайных величин x и h:
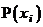
1) 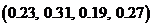 ; 2)
; 2) 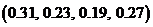 ;
;
3) 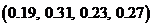 ; 4)
; 4) 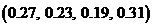 ;
;
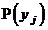
1) 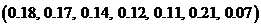 ; 3)
; 3) 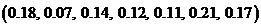 ;
;
2) 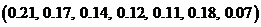 ; 4)
; 4) 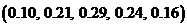 ?
?
Ответ: 3, 2.
19. (76) Каким из указанных свойствобладают взаимные спектры 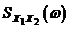 пары стационарных случайных процессов:
пары стационарных случайных процессов:
1) они являются комплексными функциями частоты;
2) вещественная часть взаимных спектров – нечетная функция частоты;
3) мнимая часть взаимных спектров – четная функция частоты;
4) амплитудный спектр – нечетная функция частоты?
Ответ: 1.
20. (79) О каких «больших числах» идет речь в законе больших чисел:
1) о больших величинах исследуемых неслучайных чисел;
2) о больших величинах исследуемых случайных чисел;
3) о большом числе исследуемых неслучайных чисел;
4) о большом числе исследуемых случайных чисел
Ответ: 4.
2. Комплексное задание:
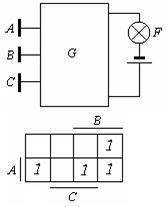
| Блок 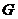 представляет собой комбинационную схему, содержащую различное число нормально разомкнутых и нормально замкнутых контактов, соединенных между собой проводами и случайно независимо друг от друга переключаемых кнопками представляет собой комбинационную схему, содержащую различное число нормально разомкнутых и нормально замкнутых контактов, соединенных между собой проводами и случайно независимо друг от друга переключаемых кнопками 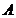 , , 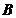 и и 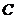 с вероятностями с вероятностями 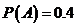 , , 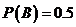 , , 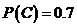 . Логика работы схемы задана картой Карно. Какова вероятность горения лампочки F:
1) 0. 27; 2) 0. 35; 3) 0. 41; 4) 0. 53? . Логика работы схемы задана картой Карно. Какова вероятность горения лампочки F:
1) 0. 27; 2) 0. 35; 3) 0. 41; 4) 0. 53?
|
Решение.
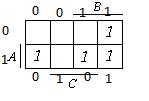
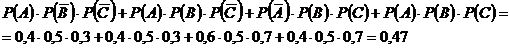
| А | В | С | 
|
Тогда вероятность горения лампочки 1-0, 47=0, 53.
Ответ: 4.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|