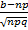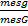- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
49 вопрос. Простейший поток событий.
| 48 вопрос. Основные понятия систем массового обслуживания. При решении практических задач часто приходится сталкиваться с системами, предназначенными для многоразового использования с решением однотипных задач. Так же системы называются системами массового обслуживания. Примерами являются магазины, парикмахерские, ремонтные мастерские. Каждая такая СМО состоит из определенного числа обслуживающих единиц. Заявки СМО на обслуживание поступают не регулярно, а случайно, образуя случайный поток заявок. Случайные характеристики потока заявок и случайного время обслуживания приводит к тому, что СМО загружена не равномерно, могут быть как очереди заявок, так и простые СМО. В связи с этим существует след классификация СМО: СМО: 1) СМО с отказами 2) СМО с очередями А)неограниченная очередь Б)ограничена длина очереди В)ограничено время пребывания в очереди. В СМО с отказами заявка, поступившая в момент, когда все каналы заняты получает отказ в обслуживании и покидает систему необслуженной. В СМО с очередями заявка в такой же ситуации становится в очередь. Очередь может быть неограниченной длины, либо с ограниченной длиной очереди, либо ограниченной временем пребывания в очереди. В качестве показателя эффективности СМО в зависимости от их типа выделяют: 1) Вероятность отказа в обслуживании 2) Средняя длина очереди 3) Среднее время пребывания в очереди 4) Среднее время обслуживания и т. д. |
49 вопрос. Простейший поток событий. По своей сущности процесс работы СМО представляет собой случайный процесс с дискретными состояниями и непрерывным временем. В отличии от цепей Маркова где время дискретное. Это означает, что возможные состояния системы S0, S1, …. Sn известны и переход из одного состояния в другое происходит мгновенно (скачком) в случайный момент времени. В процессе работы СМО, ее анализ проще представить, если использовать графическую схему называемую графом состояния системы. Например, если система может быть в следующем состоянии: S0-все каналы свободны, S1- один занят, остальные свободны, S2—2 занято, остальные свободны……Sn– все каналы заняты. Тип СМО – система с отказами, тогда граф состояний имеет вид:
Стрелками указаны возможные переходы из одного состояния в другое. Основными факторами перехода системы из одного состояния в другое является входящий поток заявок и поток обслуживания заявок. Под потоком событий понимаются последовательность однородных событий, следующих один за другим в случайные моменты времени. Основная характеристика потока- это его интенсивность х(t), которая представляет собой среднее число событий, поступивших в единицу времени в момент t. Поток событий называется стационарным, если его временные характеристики не зависят от времени. В частности β (t)=β =const. Поток событий называется потоком без последствия, если для любых непересекаемых временем интервалов Т1 и Т2 число событий, поступающих на один из их не зависит от того, сколько событий поступило на другой. Поток событий называется ординарным, если вероятность попадания намалый интервал времени дельта t 2-х и более собственно пренебрежимо мала по сравнению с вероятностью попадания на дельта t одного события. Иначе поток ординарен, если собственно появляется по одиночке, а не группами. Опред 1: поток событий называется простейшим( Пуассоновским), если он одновременно стационарен, однороден и не имеет последствия. Рассмотрим по оси времени простейший поток, как неограниченную последовательность случайных точек. µ t Β Показано, что для простейшего потока число событий точек, попадающих на интервал времени β подчиняется закону Пуассона. Pm=(µβ )me-µβ /m! Так же доказано, что Т- интервал времени между 2-мя соседними событиями простейшего потока имеет показательное распределение. F(t)=1-eµt M(t)=1/µ D(t)=1/µ2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3. Случайное событие. Классификация событий. Случайным соб. (просто событием)-наз-ся любой факт, который при осуществлении совокупности усл-ий может либо произойти либо нет. Пример1: выйгрыш авто по билету денежной лотереи Пример2: выход бракованного изделия с конвеера предприятия. Обозначения: Осуществление совокупн. условий--- произведено испытаний. Событие-обознач. прописными буквами A, B, C (при необх. с индексами) *Если в испытании вместе с появлением событий А всегда происходит событие В, то говорят что событие А влечет за собой событие В, др. словами событие В включает в себя событие А и символьно обозначают Аϲ В *Два события наз-ют-несовместными, если наступление одного из них исключает появление другого в одном и том же испытании. В противном *случае события наз-ют – совместными. ( пример: с бросание игральной кости А1, А2, А3, А4, А5, А6 –вариант исхода один! *Событие наз-ся достоверным и обозн-ся буквой Омега если в рез-те испытания оно обязательно должно произойти. (Пример: при бросании игральн. костиОмега, т. е достоверное, то выпадение от 1 до 6 очков) *Событие наз-сяневозможным, обозн-сяØ, если в рез-те испытания оно вообще не может произойти. (пример: когда при бросании игральн. кости выпадает 7 очков и оно не явл-сяслуч. событием) *Из этих определений следует что достоверное и невозможное событие являя-ся неслучайным(согласно определению об случайных событиях! ) *События наз-ют равновозможными, если есть основания полагать, что в рез-те испытания ни одно из них не явл-ся более возможным чем другое. *Несколько событий образуют полную группу, если в рез-те испытания должно пройзойти одно и только одно из этих событий. (Пример: бросание игральн. кости 1очко, 2, 3, 4, 5, 6 они образуют полную группу) *Частным случаем событий, образ-х полную группу явл-ся противоположные события. *Два несовместных события, одно из которых в рез-те испытания обязательно должн произойти наз-ся противоположными. Событие противоположное событию А обозначается Ā
| 4. Классическое определение вероятности. Свойства вероятностей. В практической деят-ти важно уметь сравнивать события по степени возможности их наступления в испытаниях. Такой мерой сравнения явл-ся вероятность событий. В наст. времясущ-ет несколько определений вероятн. Определении №1 Классич. определение. Пусть исходы некоторого испытания образуют полную группу, все они равновозможны и число их конечно, такие исходы наз-ют элементарными исходами. А само испытание схемой случая. *Элементарный исход наз-ют благопритствующий событию А, еслипоявл. этого исхода влечет за собой появл-я события А. Определение №2 Вероятностью события А, наз-ся отношение числа m благоприятствующих этому событию исхода к общему числу n всех равновозможных элементарных исходов, образ-х полную группу, т. е. верна формула: P(A)=m/n Формула (1) Пример: вероятность выпадения четного числа P(A)=3/6=1/2 Формула(1) не явл-ся универсальной например ее нельзя применить если элементарные исходы не явл-ся равновозможными или когда число исходов испытаний не явл-сяконечным, а бесконечное. Поэтому в наст. время формулу(1) рассматривают не как определение, а как метод вычисления вероятности события для испытания сводящихся к схеме случаю. Из формулы(1) вытекают лед-е важное свойство вероятности событий: 1) P(Ώ )=1 (вероятность достоверности равна единице) 2) P(Ø )= 0 (вероятность невозмож. события равна нулю) 3) 0≪ P(A)< 1 (верятностьлюбогособытиязаключенамеждунулемиединицей. Т. евероятн. любогослучайногособытиябудетлежатьмежду 0 и 1. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7. Условной вероятностью Р_А (В) события В называется вер-ть этого события при условии, что событие А уже произошло. Т1(теорема умножения). Вероятность произведения двух событий равна произведению вер-тей одного из этих событий на условную вер-ть другого найденную предположений, что первое событие уже произошло. Р(ВА)=Р(А)*Р_А (В)=Р(В)*Р_В (А) (1) Замечание: теорема умножения может быть обобщена на случай произв-го конечного числа событий. Пример: P(ABCD)=P(A)*P_A (B)*P_AB (C)*P_ABC (D) Опр. 5. Событие В назыв независимой от события А, если появление события А не изменяет вер-ть события В, т. е. Р_А (В)=Р(В) Если В не зависит от А, то и А не зависит от, т. е. события взаимонезависимы. Для незав. событий А и В формула (1) упрощается: Р(АВ)=Р(А)*Р(В) (2) Т2(теорема сложения). Вероятность суммы Р(А+В) двух событий А и В равна сумме вер-тей этих событий без вер-ти их произведения. Р(А+В)=Р(А)+Р(В)-Р(АВ) (3) Если события А и В несовместны, т. е. АВ=∅, Р(АВ)=0, тоР(А+В)=Р(А)+Р(В) Следствие из теоремы: сумма вер-тей противоположных событий равна 1 А, А ̅ А+А ̅ =Ω Р(А+А ̅ )=Р(А)+Р(А ̅ )=Р(Ω )=1 Р(А+А ̅ )=1 Р(А)=1-Р(А ̅ ) А+В+С+…+К – хотя бы одно из них А ̅ *В ̅ *С ̅ *…*К ̅ - ни одно событие не происходит Т. е. указанные события яв-ся противоположными и стало быть несовм-ми Тогда по следствию: Р(А+В+С+⋯ +К)=1-Р(А̅ *В̅ *С̅ *…*К̅ ) | 8. Пусть некоторое событие А наступает на условии появления одного из несовместных событию А ….. (ребят допишите, у меня не дописано в лекции: (( ) образующих полную группу В_1, В_2, …, В_n. B_i, i=(1, n) ̅
Такие события называются гипотезами
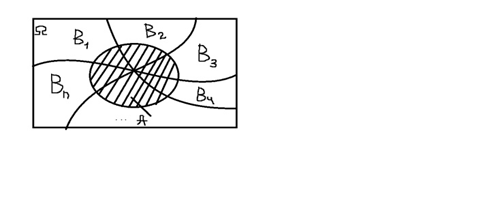 Пусть известны все вер-ти события, а также условные вер-ти события А: P_(B_i ) (A), i=(1, n) ̅
Вероятность события А, которая может наступить лишь при условии одного из несовм-ых событий B_1, B_2, …, B_(n ), образующих полную группу, равна сумме произведений вер-тей каждого из этих событий на соответствующую условную вер-ть события А, т. е.:
P(A)=P(B_1 )*P_(B_1 ) (A)+P(B_2)*P_(B_2 ) (A)+⋯ +P(B_n )*P_(B_n ) (A)=∑ _(i=1)^n▒ P(B_i ) *P_(B_i ) (A) (5) формулаполнойвер-ти.
Пример: В группе спортсменов 20 лыжн, 6 велосип. и 4 бегунна. Вероятность выполнить квалиф-ую норму: для лыж. 0, 9; для вел. 0, 8; для бегуна 0, 75. Найти вер-ть того, что спортсмен выбранный на удачу выполнит квалиф-ую норму.
Решение: А – выбранный спортсмен, который вып-илквал-ую норму.
В_1- лыжи; В_2 〖 - вел; В〗 _3- бегун
Р(В_1 )=20/30; Р(В_2 )=6/30; Р(В_3 )=4/30
Р_(В_1 ) (А)=0, 9; Р_(В_2 ) (А)=0, 8; Р_(В_3 ) (А)=0, 75
По формуле 5 находим:
Р(А)=20/30*0, 9+6/30*0, 8+4/30*0, 75=0, 86
Пусть известны все вер-ти события, а также условные вер-ти события А: P_(B_i ) (A), i=(1, n) ̅
Вероятность события А, которая может наступить лишь при условии одного из несовм-ых событий B_1, B_2, …, B_(n ), образующих полную группу, равна сумме произведений вер-тей каждого из этих событий на соответствующую условную вер-ть события А, т. е.:
P(A)=P(B_1 )*P_(B_1 ) (A)+P(B_2)*P_(B_2 ) (A)+⋯ +P(B_n )*P_(B_n ) (A)=∑ _(i=1)^n▒ P(B_i ) *P_(B_i ) (A) (5) формулаполнойвер-ти.
Пример: В группе спортсменов 20 лыжн, 6 велосип. и 4 бегунна. Вероятность выполнить квалиф-ую норму: для лыж. 0, 9; для вел. 0, 8; для бегуна 0, 75. Найти вер-ть того, что спортсмен выбранный на удачу выполнит квалиф-ую норму.
Решение: А – выбранный спортсмен, который вып-илквал-ую норму.
В_1- лыжи; В_2 〖 - вел; В〗 _3- бегун
Р(В_1 )=20/30; Р(В_2 )=6/30; Р(В_3 )=4/30
Р_(В_1 ) (А)=0, 9; Р_(В_2 ) (А)=0, 8; Р_(В_3 ) (А)=0, 75
По формуле 5 находим:
Р(А)=20/30*0, 9+6/30*0, 8+4/30*0, 75=0, 86
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9 Формула Бэйеса Следствием теорема умножения, вероятность и формула полной вероятности является теорема Бейеса. Пусть по прежнему события А может произойти только из одной из гипотез. Пусть эксперимент проведён из события А –произошло. Как при этом изменится вероятность гипотезы на этот вопрос отвечает формула Бейеса. РА(ВJ)= P(ВJ)*PВJ(A) = P(ВJ)XPВJ(A) (6) ∑ _(i=0)^n▒ 〖 P(ВJ)*PВJ(A) 〗 P(A) | 10. Повторные независимые испытания. Формула Бернулли Пусть производится несколько испытаний, причём вероятность некоторого события А не зависит от исходов других испытаний. Такие испытания называют независимыми относительно события А. Такая последовательность испытания получило название схемы Бернулли. Теорема1: Если вероятность p наступление события А в каждом испытании схемы Бернулли постоянно, то вероятность m m n-m m m n-m Pn(m)= C p (1-p) = C p q, nn m=0, 1, …., n где q=1-p Формула(1)называется формулой Бернулли. Часто возникает задача определить число m0 как навероятнейшее число наступлений события А в n независимых испытаний. Очевидно, число m0 должно определится путём решения следующей системы неравенств: Pn(m0)> =Pn(m0+1) Pn(m0)> =Pn(m0-1) C использование формулы(1) не трудно получить следующие двойное неравенство для m0: np-q< =m0< =np+p (2) np+p-(np-q)=np+p-np+q=p+q=1 Стало быть такое m0 существует. При этом если np+p целое число, то существует два невероятнейшие значения m0: m0=np+p m0=np-q | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
16. Математические операции над СВ. Две СВ Х и Y называются независимыми если закон распределения одной из них не зависит от того какие значения приняла другая СВ, в противном случае СВ называются зависимыми. Пусть Х и Y заданы своими рядами распределения: Х Х1 X2 … Xn Р Р1 Р2 … Рn Y Y1 Y2 … Yn Q Q1 Q2 … Qn 1)произведением константы С на СВ Х называют такую СВ Z которая принимает значения Zi=Cxi c Pi Z Z1 Z2 … Zn P P1 P2 … pn 2)m-ой степенью ХmСВ Х называется СВ Z значение которой определяется Zi=xim c Pi 3)суммой Х+Y называют такую СВ Z значение которой равны суммам каждого возможного значения СВ Х с каждым возможным значением СВ Y. Z=X+Y P(Z=Zij)=P(Xi+Yi)=Pij= PI*Qi если Х, Y независимы = Pi*P(yi|X=Xi) если Х, Y зависимы. Замечание: некоторые значения Хi+Yi могут повторятся, тогда вероятность значения суммы будет равна сумме соответствующих вероятностей. Х1+Y3=X2+X5; Z13=Z25 P(Z=Z13)=P1*Q3: P(Z=Z25)= P25=P2*Q5 P(Z=Z13)=P(Z=Z25)=P13+P25 4)произведением двух ДСВ Х и Y назыв. такую СВ Z=X*Y возможн. значение которых равны произведению каждого возможного значения Х на каждое возможное значение Y. P(Z=Zij)=P(XiYi)=Pij= PiQi, если X, Yнезависимые =Pi P(Y=yi|X=xi), если зависимы. Здесь также верно Замечание для суммы двух СВ
| 17. Числовые характеристики дискретной СВ. Если закон распределения ДСВ либо неизвестен, либо исчерпыв. описания не требуется ограничив. меньшими сведениями о СВ. Часто для описания СВиспольз. числа которые называются числовыми характеристиками. СВ различают числ. характер. положения (мат. ожидание, мода, медиана и т. д) и числ. характер. рассеивания (дисперсия, среднее квадратичное отклонение, коэф. вариации) Определение: Математическим ожиданием ДСВ называется сумма произведений всех ее возможных значений на соответсв. вероятность. т. е M(Х)=mx=m=x1p1+x2p2+…+xnpn=∑ xipi Замечание: если ДСВ принимает бесконечное счетное значение то мат. ожиданием называют сумму M(X)=∑ xipi Если ряд сходится, в противн. случае ДСВ мат. ожидание не имеет. Мат. ожидание является не СВ и оно характеризует некоторое среднее ожид. значение ДСВ. Мат. ожидание обладает след. св. ми: 1) М(С)=С 2) М(СХ)=С*М(Х) 3) М(X+-Y)=M(X)+-M(Y) 4) M(XY)=M(X)*M(Y), если X, Y независимые СВ Модой ДСВ называется наиболее вероятное значение ДСВ, если pk=maxpi M0(X)=Xk P(X=Xk)=Pk=max pi X=X-m -центриров. СВ M(X)=0 Определение: Дисперсией ДСВ Х называется мат. ожидание квадрата ее отклонения от мат. ожидания. т. е. D(X)=σ 2=M((X-m)2=∑ (xi-m)2pi Дисперсия обладает след. св. ми: 1) D(C)=0 2) D(CX)=C2D(X) 3) D(X+-Y)=D(X)+D(Y), если X, Y независим. СВ. Дисперсия описывает рассевание СВ относит. мат. ожидания. Средним квадратич. отклонением СВназыв. квадратный корень из дисперсии. σ (х)=σ =√ D(x) Коэф. вариации V=σ: |m|*100% В % характериз. рассеивание СВ от мат. ожидания. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
19. Непрерывной СВназыв. случ. величина Xесли её ф-ияраспред-я непрерывна в любой точке и дифференцирована всюду кроме конечного числа точек.
Плотностью распред-я вероятности будем обозначать f(x), назыв. производная от её функции распред-я. Плотность распред-я вероятности назыв. дифференциация законом распред-я НСВ. Плотность распределения вероятности для ДСВ не существует. Основные свойства плотности распред-я: 1)Ф-я f(x) всюду не отриц-я ф-я т. е. f(x)> 0 как производная неубывающей ф-ии.
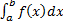
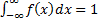 (в прямоугольнике это знак бесконечности) (в прямоугольнике это знак бесконечности)
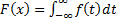
| 20. Числовые характеристика непрерывной случайной величины (НСВ). Понятие числовых характеристик введенных для ДСВ распространяется и для НСВ. Для этого от суммы требуется перейти к интегралу. Математическое ожидание для НСВ по определению находится по следующей формуле: 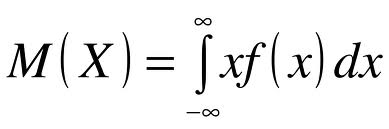 если данный несобственный интеграл сходится. Если он расходится, то матем. ожидание СВ не существует. Если областью реализации СВ является отрезок [a; b] (например, для равномерно распределенной СВ, то несобственный интеграл заменяется определенным интегралом с пределами интегрирования от а до b). Дисперсия непрерывной случайной величины: если данный несобственный интеграл сходится. Если он расходится, то матем. ожидание СВ не существует. Если областью реализации СВ является отрезок [a; b] (например, для равномерно распределенной СВ, то несобственный интеграл заменяется определенным интегралом с пределами интегрирования от а до b). Дисперсия непрерывной случайной величины: 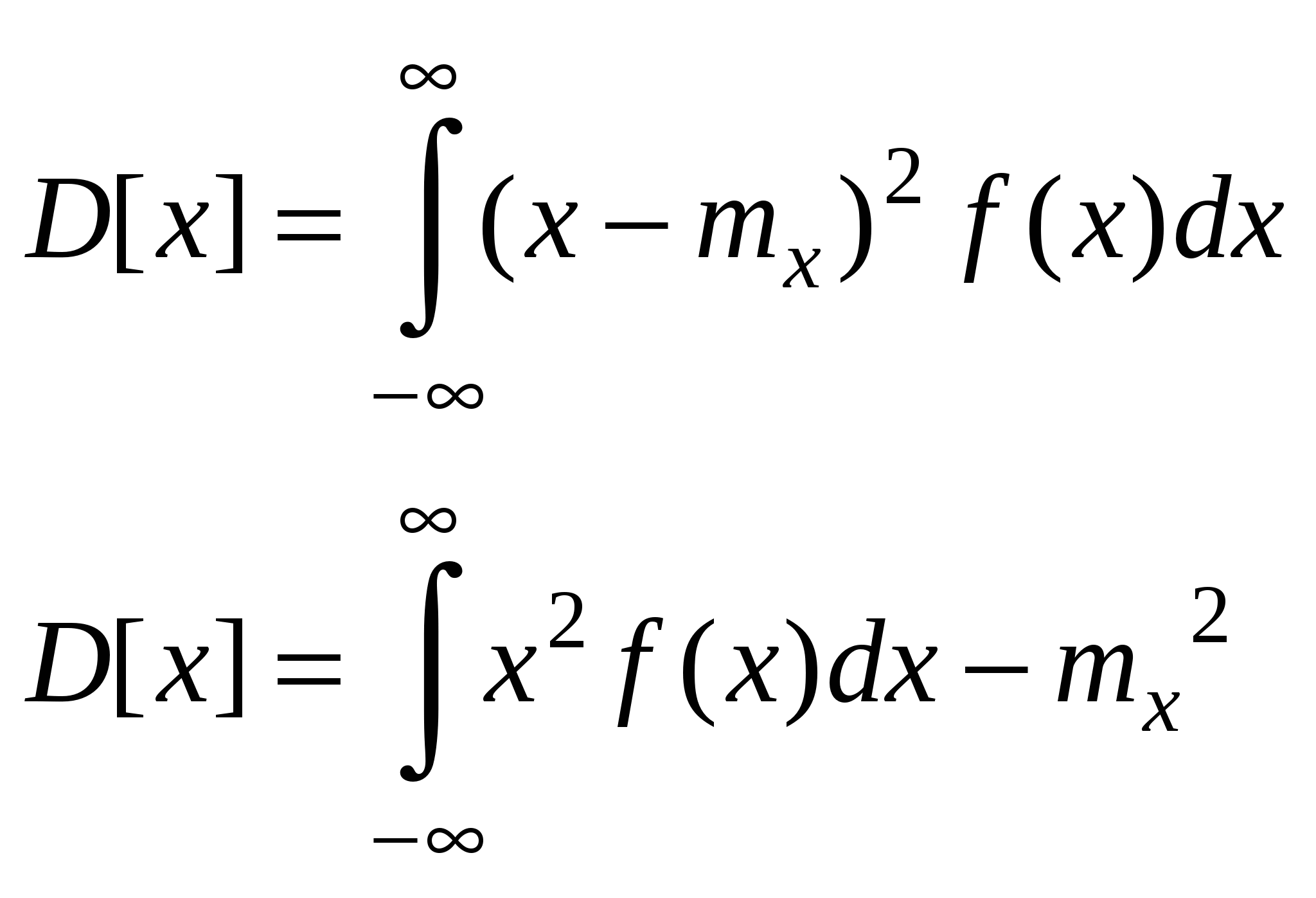 Кроме названных применяются и другие числовые характеристики. Модой СВ Х называют наиболее ее вероятное значение ДСВ или точка max.
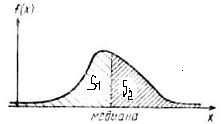
Кроме названных применяются и другие числовые характеристики. Модой СВ Х называют наиболее ее вероятное значение ДСВ или точка max.  Медианой НСВ Х называется такое значение СВ, когда выполняется равенство: Р(Х< Ме(х))=Р(Х> Ме(х))=1/2.
Медианой НСВ Х называется такое значение СВ, когда выполняется равенство: Р(Х< Ме(х))=Р(Х> Ме(х))=1/2.
 Квантилем уровня qназыв. такое значение ХqСВ Х при котором функция распределения принимает значения равное: F(xq)=P(x< xq)=q. Наиболее часто используются децили Х0. 1, х0. 2 и т. д., процентили Х0. 01, Х0. 02 и т. д. Начальным моментом К-го порядка НСВ Х называют математическое ожидание его к-ой степени Ѵ к=М(ХК). Нейтральным моментом К-го порядка НСВ называют математич. ожидание к-ой степени отклонения СВ Х от матем. ожидания: µк=М((х-m)k)=M(xk). Отсюда мат ожидание есть начальный момент 1-ой степени, К=1, дисперсия центра: D(x)=µ2, М(Х)= Ѵ 1. Третий центральный момент служит для вычисления ассиметрии: А=(µ3: G3) – они характер склонность распределения. Четвертый центральный момент служит для вычисления эксцесса Е=(µ4: G4)-3, которое характер остроконечность.
Квантилем уровня qназыв. такое значение ХqСВ Х при котором функция распределения принимает значения равное: F(xq)=P(x< xq)=q. Наиболее часто используются децили Х0. 1, х0. 2 и т. д., процентили Х0. 01, Х0. 02 и т. д. Начальным моментом К-го порядка НСВ Х называют математическое ожидание его к-ой степени Ѵ к=М(ХК). Нейтральным моментом К-го порядка НСВ называют математич. ожидание к-ой степени отклонения СВ Х от матем. ожидания: µк=М((х-m)k)=M(xk). Отсюда мат ожидание есть начальный момент 1-ой степени, К=1, дисперсия центра: D(x)=µ2, М(Х)= Ѵ 1. Третий центральный момент служит для вычисления ассиметрии: А=(µ3: G3) – они характер склонность распределения. Четвертый центральный момент служит для вычисления эксцесса Е=(µ4: G4)-3, которое характер остроконечность.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 21 Биномиальное распределение. дискретная случайная величина Х имеет биномиальное распределение с параметрами числа n, р если она принимает конечное число 0, 1, 2… n с вероятность, Если (1) видно что вероятности находятся по формуле Бернулли и биномиальный закон распределения, является закон распределения n появен. События А, в n независ. Испытаний в каждом из котор. Данное событие появится. Ряд распределения данной случ. величины имеет вид xᵢ 0 1 2 … n
Не трудно показать что СВ X имеет след. Числовые характеристики. M(x)=np D(x)=npq q=1-p такая мода СВ выделяется из неравенства np-q≤ M_0 (x)≤ np+q некоторые СВ распределенные по биномиальному закону имеют единственную моду (унимодальные), а некоторые две равные по вероятности моды (бимодальные).
| 22 Дискретная СВ X имеет распределение Пуассона с параметрами если она принимает значение 0, 1, 2… n (бесконечное множество) с вероятностьюP=(x=m)=P_m (⋏ )=(⋏ ^m e^(-⋏ ))/m! , m=0, 1, 2.. (2)
Из (2) видно что вероятности определяются с использованием функции Пуассона.
Ряд распределения представляет ∞ -ную таблицу
Числовые характеристики M(x)=⋏ D(x)=⋏, смыслпараметра⋏ Данные СВ широко используются при моделировании систем массового обслуживания, а также технич. систем, отказы котор. часто имеет распределение Пуассона. Отметим следующие распределения Пуассона. Если X и Y- распределение по закону Пуассона, то их сумма (X+Y) также распределена по закону Пуассона. При p→ 0, n→ np=⋏ =const Биномиальное распределение стремится к распределению Пуассона. Отсюда вычисление по формуле Бернулли приближено заменяются вычислениями по формуле Пуассона. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 23. Геометрическое распределение ДСВ X имеет геометрическое распределение с параметром p, если она принимает значения 1, 2, 3, …, n,.. (бесконечное, но счётное множество) с вероятностью P(x=m) =pqm-1, q=1-p, 0< p< 1, m=1, 2,... . Ряд распределения представляет собой бесконечную таблицу
| 24. Равномерный закон распределения.
НСВ X имеет равномерное распределение на отрезке [a; b] если её плотность распред-я постоянна на этом отрезке и равна 0 вне его.
(рис)
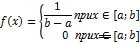 f(x)= F´ (x)
f(x)= F´ (x)
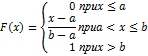
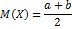
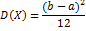 Случайная величина X имеющая равномерное распред-е на отрезке [0; 1], которая назыв. «случайное число» от 0 до 1 используют часто в качестве генератора случ. чисел, а также для получения генерирования распределения других законов распред-я.
Случайная величина X имеющая равномерное распред-е на отрезке [0; 1], которая назыв. «случайное число» от 0 до 1 используют часто в качестве генератора случ. чисел, а также для получения генерирования распределения других законов распред-я.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
25. Нормальный закон распределения Данное распределение наиболее часто используется на практике. Не прерывание СВ Х имеет нормальный закон распределения закон Гаусса с параметрами m и ʛ, если ее плотность распределения имеет вид:
m
m M(X)=m; D(X)=
Для того, чтобы указать что Х имеет нормальный закон распределения используют короткую запись: Х˞ N(m; ʛ 2). В частном случае, когда m=0; ʛ 2=1, X˞ N(0; 1), говорят о стандартном нормальном распределении и плотность распределения симметрична, относительна оси Х.
кривая
Для нормальной распределения СВ справедливо 3х сигма (ʛ ): P(m-3 ʛ ≤ X≤ m+3 ʛ )=0, 9973/
P(x1≤ X≤ x2)= Замечание: в некоторых приложениях функция Лапласа определяется по след. Формуле:
| 26. Показательный закон распределения
Непрерывные СВ Х имеет показательный (экспонициальный) закон распределения с параметром ʎ, если ее плотности распределения имеет вид:
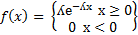 Если воспользоваться формулой связывающей функцию распределения с плотностью, то не трудно получить след. Формулу для распределения:
Если воспользоваться формулой связывающей функцию распределения с плотностью, то не трудно получить след. Формулу для распределения:
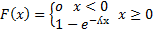
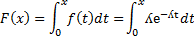
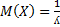 ; ; 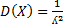 ; ;  Показательное распределение широко применяется при моделировании систем массового обслуживания и теории надежности тех. Систем.
Показательное распределение широко применяется при моделировании систем массового обслуживания и теории надежности тех. Систем.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
27)Понятие многомерной СВ. Закон распределения вектора. Упорядоченный набор С Вназыв. многомерной СВ, системойслучайныйх величин и n-мерным случ вектором ЧВ Хi- компоненты вектора могут быть либо дискретными и принимает конечное число значений, то закон распределения случ вектора можно задать в виде матрицы или таблицы, которая будет аналогом ряда распределения одномерной СВ. Такая таблица для двумерного случ вектора (Х, Y).
Pij=P((X=Xi)(Y=Yj)) Qj=∑ Pij, j=1, m Pi=∑ Pij, i=1, n ∑ Pi=∑ qj=1 Числовой столбец ∑ Pij(pi) вместе со столбцом Xi представляют ряд распределения компонента Х, т. е:
Cтрока ∑ Pij(qi) вместе со строкой yi образует ряд распределения однмернойслцч величины y, т. е:
Если зафиксировать значение одного из случ аргументов, например Y=yi, то полученное распределение другого случ аргумента Х, назыв условным распределением Х при Y=yi. Вероятность X=xi при условии что событии Y=yj произошло назыв условной вероятность и вычисляется:
P(x=xi/yi)= =P(x=xi)(Y=yi)/P(Y=yi)=Pij/qj
P(Y=yj/Xi)= =P((x=xi)(Y=yi))/P(X=Xi)= Pij/Pi
| 15)Законы распределения дискретной случ величины
Наиб полным исчерпывающим описанием СВявл её закон распределения.
Определение: Законом распределения ДСВ назыв всякое соотношение, устан связь между возможными значениями СВ и соотв им вероятностям. Закон распределения ДСВ может быть задан в виде матрицы, графически или аналитически. Пусть дискретслуч значение Xx1, x2, …., xn; p(x=xi)=pi, i=1, n
p(x=xi), i=1, n- события несовместны и образуют полную группу. ∑ Pi=1 Приведенная таблица со св-ом что ∑ Pi=1, назыв рядом распределения ДСВ. Иногда законы распред ДСВ задают в виде матрицы:
X=(x1 x2 xn) p1 p2 pn законы распред ДСВ можно изобразить графически, не нарушая общности рассуждения, будем считать, что возможное значение Xi ДСВ ранжированы по возрастанию Построенный график назыв многоугольником или полигоном распред вероятности ДСВ. Аналитическое задание закона распред ДСВ выраж в записи конкретной формулы для вычисления вероятности принятия ДСВ своих возмож значений. Например в схеме независимых испытаний вероятность события А ровно m раз в n испытаниях опред формулой: Pn(m)=C*p (1-p), m=0, 1, …, n
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
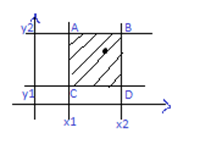
28. Функция распределения многомерной СВ и ее св-ва. Функция распределения вероятн. n-мерн. случайного вектора функции F(x1, x2.. xn) выраж. вероятн. совместн. выполн. неравенств x1< x1, x2< x2… xn< xnт. еF(x1, x2…xn)=P(x1< x1, x2< x2, …, xn< xn). в частном случае (n=2) F(x, y)=P(X< x, Y< y)
Геометрич. средн. распред. F(x, y)выржает вероятность попадания случайной точки (X, Y) бесконечн. квадрат лежащий ниже и левее точки M (X, Y). Правая верхняя граница этой области в квадрат не включ. т. е F(X, Y) явл. непрерывной слева по кажд. арг., если компоненты X и Y явл. ДСВ, то среднее распределение такой двухмерной СВопред. по форм. F(X, Y)=∑ ∑ Pij Суммирование по i выполн. по тем значен. i, когда xi< x, по j выполн. когда yj< y. Отметим св-ва функции распределения двумерного случ. вектора: 1) F(x, y) явл. не отриц. функцией, ее значение наход. 0≤ F(x, y)≤ 1 2)функция распределения F(x, y) явл. не убывающ. функц. своих аргументов т. е при х2 > x1 → F(x2, y)≥ F(x1, y) при y2> y1 F(x, y2)≥ F(x, y1) 3) Если хотя бы 1 из аргументов обращ. в -∞ то функция распред. =0 F(-∞, y)=F(x, -∞ )=F(-∞, -∞ )=0 4)Если один из аргументоа обращается в +∞, то функция распред. F(x, y)= функции распред. др. аргумента. т. е F(∞, y)=F2(y); F(x, ∞ )=F1(x). 5)Если оба аргумента обращ. в ∞, то функция распред. =1 F(∞, ∞ )=1 Геометр. функц. распред. двухмерн. случ. вектора представл. собой некотор. поверхность в пространстве с указ. для ДС вектора это будет ступенчатая поверхность со скачками в угловых точках табл. распред. вероятн. Зная F(x, y) произв. прямоугольн. ABCD
P(X1≤ X≤ X2) (y1≤ Y≤ y2)=F(x2, y2)-F(x1, x2)-F(x2, y1)+F(x1, y1)
42. Закон больших чисел. Теорема Чебышева. Теорема: если последовательность попарно независимой СВ имеет М(х)=
Отметим смысл теоремы Чебышева при выполнении ее условия, если n- велико, то СВ Из теоремы Чебышева не следует выполнение этого предела: В смысле классичопредел-я предела измат анализа. СВ В частном случае, если все СВ
Рассмотрим применение т. Чебышева для решения след практич задачи: обычно для изменения некотфизич величины производят несколько измерений этой величины на нескольких реальных объектах и их сред арифметич использует для определ-я искомого размера. В каких случаях такой подход оказ-сяоправданным? На этот воп отвечает частный случай т. Чебышева. Если рез-ты измерений обозначать так: Х1, Х2, …, Хn, то к ним можно применить теорему, если: 1. Хi попарно независимые, то это условие выпол-ся, если рез-ты измер-я не зависят от других. 2. СВ Хi имеют одно и тоже М(х). Это будет выпол-ся, если измер-я производ-ся без систематич ошибок (одного знака). 3. D(x) равномерно ограничены. Это условие будет также выпол-ся, если прибор обеспечивает одинак точку соизмер-я.
|
41. Неравенство Маркова и Чейбышева.
Под законом больших чисел в широком смысле понимается общий принцип согласно которому совокупное действие большого числа случайных факторов приводит к результату части независящему от случая. Под законом больших чисел в узком смысле понимается ряд теории в которых устанавливается факт приближения средних характеристик большого числа испытаний к некоторым постоянным. Прежде чем формулировать эти теоремы сформулируем вспомогательные неравенства Маркова и Чейбышева.
Теорема1: (Неравенства Маркова)
Если СВ Х принимает неотрицательное значения и имеет мат. ожидание, то для любого А> 0 определено неравенство.
Р(Х> А)< =М(Х)(1)
А
Т. к. события (Х> А) и (Х< =А) явл-ся противоположным то существует 2 редакций неравенства Маркова а именно Р(Х< =А)> =1-M(X) (2)
A
Теорема2: (Неравенства Чейбышева)
Для любо СВ Х имеющей мат. ожиданиеM(Х)и D(X) для ¥ E> 0 справедливо неравенство P(/Х-М(Х)/> =E)< =D(X) (3)
2
E
Поскольку событие /X-M(X)/< E
/X-M(X)> =E
P(/X-M(X)/< E)> =1-D(X) (4)
E
Неравенство Чейбышева имеет для практики ограниченное значение, т. к зачастую даёт грубую а
2
порой и тривиальную оценку. Например, если дисперсия СВ> E, то D(X) 1-D(X)< 0
2
E
Но вероятность случайного события по определению явл-ся не отрицательной величиной и неравенство (4) утверждает что явл-ся тривиальной. Однако для теории значения неравенств Чейбышева весьма велико, т. к с его помощью доказывается теоремы закона больших чисел.
43. Закон больших чисел. Теорема Бернулли.
Теорема: если в каждом из n-независим испыт-й вер-тьpпоявл-сянекот события А постоянна, то относит частота  появл-я события А в n-испытаниях сходится по вероятности числу р, т. е. для любого полож. появл-я события А в n-испытаниях сходится по вероятности числу р, т. е. для любого полож. 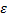 . .
 47. Марковские случайные процессы.
Случайные процесс протекающей в некоторой системе с возможными состояниями S1, S2,.., Sn….
Называется Марковским или случайным процессом без последействия если для любого момента времени t вероятные характеристики процесса в будущем t0(t> t0) определяется только его состоянием в момент t0 и не зависят от того когда и как система пришла это состояние т. е не зависит от поведения системы в прошлом (t< t0).
Пример: В грубом приближении Марковского процесса явл-ся игра в шахматы.
Марковским случайным процессом с дискретными состояниями и дискретным временем (целью Маркова) наз-ся Марковский процесс в котором его возможные состояния S1, S2, …, Sm можно заранее перечислить, а переход из одного состояния в другое происходит мгновенно в определённые моменты времени t0, t1, t2, … называемые шагами. Если обозначить через pij вероятности перехода системы из состояния Si в состояние Sj то систему можно охарактеризовать матрицы перехода которые имеют вид:
P11 p12…p1m
P1= ( P21 p22…p2m )
Pm1 pm2…. pmm
m
Не трудно показать что ∑ pij=1
J=1
Обозначим через pij(n)-вероятность того что за n шагов система из состояния Si перейдёт в состояние Sj. Не трудно видеть что pij(1)=P1.
Для того чтобы найти Pij(n) воспользуемся равенством Маркова.
m
Pij(n)=∑ Pir(k)prj(n-k)
r=1
Когда система из состояния Siв начале переходит в промежуточное состояние Sr за k шагов и затем из Sr в Sj(n-k) шагов. Предположим n=2, K=1, тогда по равенству Маркова:
m 2
Pij(2)=∑ pir91)prj(1)=P1*P1=P1
n=1 3
Возьмём n=3 и k=2 тогда не трудно показать что Pij(3)=∑ pir(1)*prj(2)=P1*P2=P1
n
Pij(n)=P1
47. Марковские случайные процессы.
Случайные процесс протекающей в некоторой системе с возможными состояниями S1, S2,.., Sn….
Называется Марковским или случайным процессом без последействия если для любого момента времени t вероятные характеристики процесса в будущем t0(t> t0) определяется только его состоянием в момент t0 и не зависят от того когда и как система пришла это состояние т. е не зависит от поведения системы в прошлом (t< t0).
Пример: В грубом приближении Марковского процесса явл-ся игра в шахматы.
Марковским случайным процессом с дискретными состояниями и дискретным временем (целью Маркова) наз-ся Марковский процесс в котором его возможные состояния S1, S2, …, Sm можно заранее перечислить, а переход из одного состояния в другое происходит мгновенно в определённые моменты времени t0, t1, t2, … называемые шагами. Если обозначить через pij вероятности перехода системы из состояния Si в состояние Sj то систему можно охарактеризовать матрицы перехода которые имеют вид:
P11 p12…p1m
P1= ( P21 p22…p2m )
Pm1 pm2…. pmm
m
Не трудно показать что ∑ pij=1
J=1
Обозначим через pij(n)-вероятность того что за n шагов система из состояния Si перейдёт в состояние Sj. Не трудно видеть что pij(1)=P1.
Для того чтобы найти Pij(n) воспользуемся равенством Маркова.
m
Pij(n)=∑ Pir(k)prj(n-k)
r=1
Когда система из состояния Siв начале переходит в промежуточное состояние Sr за k шагов и затем из Sr в Sj(n-k) шагов. Предположим n=2, K=1, тогда по равенству Маркова:
m 2
Pij(2)=∑ pir91)prj(1)=P1*P1=P1
n=1 3
Возьмём n=3 и k=2 тогда не трудно показать что Pij(3)=∑ pir(1)*prj(2)=P1*P2=P1
n
Pij(n)=P1
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
52. Системы массового обслуживания с отказами. Рассмотрим n-канальную (с каналами одинаковой производительности) систему с отказами. Заявка на поступившие в системе и заставшая все каналы занятыми покидает систему необслуженной. В системе действуют два простейших потока: входной поток заявок, с интенсивностью λ (константа) и поток обслуженных заявок с одного канала с интенсивностью µ. Требуется найти предельные вероятности состояний системы (если они существуют), а так же показатели эффективности системы, к которым относят абсолютную пропускную способность A, т. е. среднее число заявок, обслуженных системой за единицу времени. Р отказа, т. е. вероятность того, что заявка не будет обслужена. Q – относительная пропускная способность, т. е. средняя доля пришедших заявок, которая будет обслужена. К (с чертой) – среднее число занятых каналов, характеристика показывает степень загрузки СМО. Поставленную задачу называют задачей Эрлонга. Система имеет n+1 каналов, S0 – все каналы свободны, простое состояние, Sk – k= изменяется от 1 до n, в системе заняты k каналов, n-k каналов свободны. Граф состояния системы имеет следующий вид: Система переходит из левого состояния в правое с одной и той же интенсивностью λ, интенсивность же потока обслуживания, переводящего систему из любого правого состояния в левое зависит от самого состояния. Например, если система находится в S2 (2 канала заняты) тогда потоки обслуживающие каждый канал порождают свой поток, с интенсивностью µ, в итоге суммарная интенсивность будет 2µ. Из графа видно, что это процесс гибели разложения и можно записать формулы, для вычисления предельных вероятностей, например: Р0= (1+(1: µ)+ (λ 2: 2µ)+( λ 3: (1*2*3*µ3))+…+( λ n: (1*2*…n*µ*n))-1. Введем следующую величину, которую называют приведенной интенсивностью входного потока и обозначаем как: ρ («ро»). Она представляет среднее число заявок, переходящей в переходящих во время обслуживания одной заявки, тогда формула для p0 примет вид: р0= (1+ ρ +(S2: 2! )+(S3: 3! )+…+(Sn: n! ))-1, р1=ρ *Р0, р2=(ρ 2: 2! )*р0, р3=(ρ 3: 3! )*Р0, рn= (ρ n: n! )*p0. Далее можно определить показатели эффективности СМО: Ротказа=Рn=(ρ n: (n! *p0), Q=1-Pотказа - это относительная пропускная способность, А=Qλ – абсолютная пропускная способность, K(с чертой)=А: µ
| 64 вопрос. Статистическая гипотеза и общая схема ее проверки.
Прежде чем, изучать методы проверки гипотез сформулируем принцип практической уверенности на котором они основаны: если вероятность события А в данном испытании очень мала, то при однократном выполнении этого испытания можно быть уверенными в том, что событие А в нем не произойдет. Статистической гипотезой называется любое предложение о виде закона распределения СВ, либо предположение о параметрах известных распределений. Выдвинутую гипотезу называют основной или нулевой, и обозначают обазначают Н0. На ряду с ним всегда рассматривают альтернативную, конкурирующую гипотезу Н, которая противоречит гипотезе Н0.
Н0: М(х)=10
Н1: М(х) не равно 10
Н1: М(х)> 10
Н1М(х)< 10
H1M(x)=15
Гипотеза Н0 называется простой, если она содержит одно конкретное предположение. Н0: θ =θ θ из конечного или бесконечного числа гипотез. Например: Н0: θ > θ θ .
Проверку или тестирование гипотезы не выполняют на основе имеющихся выборочных данных. Если она им противоречит, то гипотезу Н0 отклоняем, в противном случае гипотезу Н0 принимаем. Для этого возможны 2 ложных решения, которые совершаются с вероятностями α и β.
Вероятность α совершить ошибку 1 рода, т. е. отвергнуть гипотезу Н0, в то время как она верна назыв. Уровнем значимости правила принятия решения. Вероятность ошибки 2 рода Н0 будет принят, в то время, как она не верна обозначают β. Вероятность 1-β назыв. мощностью правила выбора решения. При принятии решения по гипотезе Н0 требуется минимизировать ошибки 1 и 2 рода, но одновременно уменьшение α и β достигнуть не удается, т. к. они противоречат друг другу. Рассмотрим как технически выполняется тестирование Н0. Пусть выдвинута гипотеза Н0. Для проверки этой гипотезы используется специально подобранная для некоторой СВ к, законы проведения которых, либо точно известны, либо приближенно, но тоже достаточно сложно. СВ к назыв. статистическим критерием или статистикой. К=К(х1, х2, ……хn) Cтатистический критерий представляет собой нек-ю функцию элементов выборки к, если из генеральной совокупности извлекается некоторая выборка СВ к получает реализацию Кнаб. Множество всех возможных значений СВ к разбивается на 2 непересекающихся подмножества: одно из них содержит значение критерия К, когда гипотеза Н0принемается, а другое, те значения К, при которых гипотеза Н0 отвергается. Первое подмножество назыв. областью принятия гипотезы Н0, а второе подмножество- критическое. Точки, разделяющие указанные подмножества назыв. критическими. В зависимости от вида альтернативной гипотезы 1 различают 3 вида критической области: -двусторонняя, -правосторонняя, -левосторонняя. Критическую область выбирают так, чтобы вероятность попадания в нее СВ К была равна вероятности ошибки 1 рода α, т. е. уровню значимости. α =(0, 1-0, 001) В этом случае вывод о судьбе гипотезы не выполняется с надежностью γ =1-α. Поскольку закон распределения К известен, то без труда находятся границы критической области, т. е. критические точки. Если уровень значимости найден, то критические точки находятся: Н0 F(k(H0) Н1 Н1 α /2 Kkp1 Kkp2 к P(k< kkp1)P(k> kkp2)=1/2. H1: θ не равно θ θ P(k> kcp)=α H1: θ > θ θ P(k< kcp)=α H1: θ < θ θ . | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
13. Если вероятность р наступления события А в каждом испытании постоянна отлична от 0 и 1, то вероятность того, что в n независимых испытаниях событие Апоявл. В пределах от А до В(включит) при достаточно большом n приближенно равна: Р(а≤ m≤ в) Ф(х)= Функция Ф(х) определяемая формулой наз. Функцией Лапласа и вычислено в спец. Табл.
| 14. Случайная величина в теории вероятностей, величина, принимающая в зависимости от случая те или иные значения с определёнными вероятностями. Так, число очков, выпадающее на верхней грани игральной кости, представляет собой С. в., принимающую значения 1, 2, 3, 4, 5, 6 с вероятностью 1/6 каждое. Если С. в. Х принимает конечную или бесконечную последовательность различных значений, то её распределение вероятностей (закон распределения) задаётся указанием этих значений: x1, x2,..., xn,... ДСВ может быть задана рядом распределения, когда каждому отдельному изолированному знач. ДСВ ставится в соответ. вероятность. Для НСВ это невозможно, т. к. НСВ бесчисленное множество значений, ряд распределения невозможен. Для описания закона распределения НСВ возможен др. подход связанный не с опред. Вероятностью Р=(Х=х), когда СВ Х принимает конкретное фиксированное знач. х, а с вероят. Знач. Р(Х< х), когда Х принимает значение строго меньше нек-ого фиксир. Знач. х. НСВ наз. Случ. Величина Х, если ее ф-ия распределения непрерывна в любой точке и дифференцируема всюду, кроме конечного числа точек. Ф-ей распр. Вероятностей СВ Х назыв. Ф-ияF(x) определяющая вероят. того, что СВ Х примет значение строго меньше х, т. е. F(x)=P(X< x) Ф-ияF(x) назыв. Интегральным законом распределения закона СВ. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5. Статистической вероятностью событий А назыв. относительная частота повторения этого события в n производимых испытаниях, т. е. Ṕ (А)=W(А)= Если в одинаковых условиях производить серии испытаний число к-ых должно быть велико, то относит. Частота события обнаруживает св-во устойчивости. Этосв-во состоит в том, что в различных сериях испытаний относит. Частота изменяется мало и колеблится около нек-ого числа-это число и явл. вероятностью появл. События в испытании. Геометрич. Вероят. события А назыв отношение площади области g благоприятствующей событию А к площади всей области G, т. е. Р(А)= Область на к-ую падает случайная точка может быть одномерной и трехмерной, отсюдадлина, площадь, объемобознач. Общим символом mes.
38. Распределения Хи-квадрат. Распределение χ 2(k) ckстепенями свободы называется распределение суммы квадратов k независимых СВ распределен. по стандартному нормальному закону. т. еχ 2(k)=∑ Zi2когда Z~N(0, 1) независимые СВ. M(χ 2)=k D(χ 2)=2k
k→ ∞ χ 2→ N(m, σ 2)
| 6. Суммой А+В двух событий А и В назыв. Событие состоящие в появлении хотя бы одного из этих событий, т. е. либо появл. События А либо появл. События В либо обоих вместе.
Произведением 2ух событий А и В назыв. Событие состоящее в совместном появлении событий А и В.
Разностью 2ух событий А и В (А\В) назыв. Событие, если А происходит, а событие В не происходит.
Геометрически действие над событиями хорошо иллюстрируются диаграммами Венна.
 

| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|
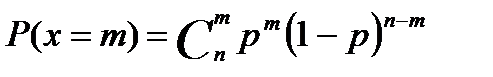 ,
, 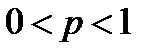 ,
, 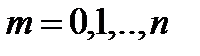 , (1)
, (1)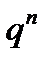
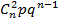
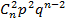
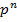
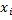
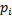
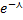
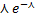

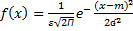
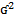 ; ʛ (X)= ʛ
; ʛ (X)= ʛ 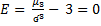 ;
; 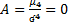
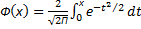 - функция Лапласа
- функция Лапласа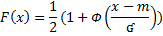
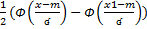 .
. 
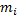 и D(
и D( 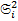 равномерно огранич. ( т. е. непревышающиеобщий постоянные…, то среднее арифметич этих СВ сходится по вероят-ти к сред арифметич их мат ожид-й).
равномерно огранич. ( т. е. непревышающиеобщий постоянные…, то среднее арифметич этих СВ сходится по вероят-ти к сред арифметич их мат ожид-й). 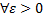 справедливо
справедливо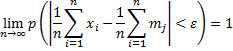
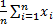 сколь угодно мала, отлич-ся от неслуч величины
сколь угодно мала, отлич-ся от неслуч величины 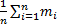 .
. 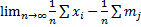
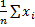 в отдельных случаях даже при n
в отдельных случаях даже при n 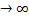 может существенно отличаться от мат ожид-я, но вер-ть отклонения СВ
может существенно отличаться от мат ожид-я, но вер-ть отклонения СВ 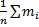 ) ед. равна 1. В этом и заключается понятие сходимости по вероятности.
) ед. равна 1. В этом и заключается понятие сходимости по вероятности. 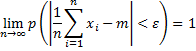
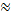 Ф(
Ф( 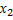 )-Ф(
)-Ф( 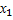 )
)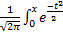 dt
dt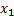 =
= 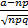 ;
; 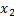 =
=