Распределение Стьюдента

Случайная величина 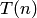есть отношение двух независимых случайных величин 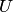и 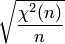, то есть

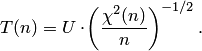
Распределение случайной величины 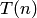называется распределением Стьюдента с 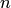степенями свободы. Его плотность задаётся формулой

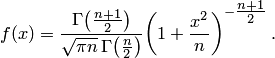
Математическое ожидание и дисперсия случайной величины, подчинённой распределению Стьюдента 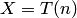, есть

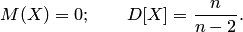
Кривые распределения Стьюдента (для различных значений ) изображены на рис. 26.

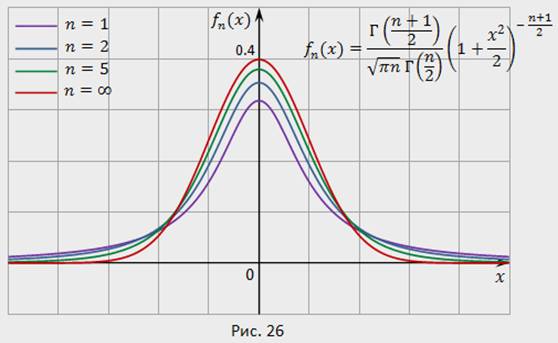
При увеличении распределение Стьюдента стремиться к нормальному, более того, стандартизованному нормальному (то есть с нулевым математическим ожиданием и единичной дисперсией). Распределение Стьюдента широко применяется в задачах математической обработки измерений.

Задача№1 Найти симметричный интервал, в который случайная величина, распределенная по закону Стьюдента с 12-ю степенями свободы, попадает вероятностью 0, 9.

Решение. Очевидны соотношения:

P(–x < t < x) = P(|t| < x) = 1 – P(|t| ≥ x) = 0, 9.

Из последнего равенства следует:

P(|t| ≥ x) = 0, 1, (n = 12).

Определяем из таблицы: x=1, 782. Нестрогое неравенство в скобках в левой части последней формулы нас не должно смущать, так как мы имеем дело с непрерывной случайной величиной, и вероятность того, что она примет конкретное значение, равна нулю.

Задача№2 Найти значение x из условия P(t > x) = 0, 995, где t – случайная величина, распределенная по закону Стьюдента с 12-ю степенями свободы.

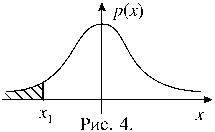
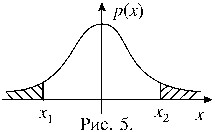
Решение. На рисунке 4 изображен график плотности распределения Стьюдента с 12-ю степенями свободы. Вероятность того, что случайная величина примет значение из области справа от точки x1 равна 0, 995, следовательно, в область левее этой точки случайная величина попадает с вероятностью 0, 005. Чтобы найти x1, рассмотрим две симметричные области, изображенные на рисунке 5. Допустим, что в каждой из этих областей значение случайной величины оказывается с вероятностью 0, 005. Тогда получаем: x1= –x, x2=x, причем x определяется из условия P(|t|> x)=0, 01. Из таблицы 2 находим: x=3, 055. Теперь можно выписать ответ задачи:

P(t > –3, 055) = 0, 995.