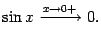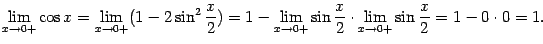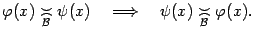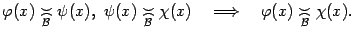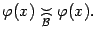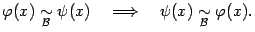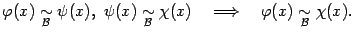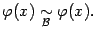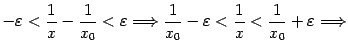- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Пусть функции f(x) и g(x) непрерывны в точке х0. Тогда функция f(x) не равная g(x), f(x)g(x) и (если g(x) не равно 0) непрерывны в точке x0.
1. Промежутки, окресности. Верхняя и нижняя грань числового множества. Точные грани и их свойства.
Интервалы и отрезки - это конечные числовые промежутки. Промежутки бывают следующих типов:
Интервал: строгое неравенство(a< X< b); Отрезок [a; b]; Открытый справа([a; b)) и слева.
: ε –окрестностью числа а называется множество чисел х удовлетворяющие неравенству
 a-ε < x< a+ε Û |x-a| Û (////·////) x Û Оε (а)
a-ε < x< a+ε Û |x-a| Û (////·////) x Û Оε (а)
Числовое множество называется ограниченным сверху если все числа данного числового множества меньше некоторого числа В
Точная верхняя грань-найменьшая из всех верхних граней(sup{X}). inf{X}-точная нижняя грань
Свойства точных граней: Теорема:
M=Sup{X} необходимо и достаточно выполнение: 1)x> M=> x не принадлежит X. 2)Для любого С < M есть хотя бы 1 х из Х => C< x< =M
Док-во
1Необходимость. Дано M=Sup{X} Доказать 1, 2. Док-во
1. т. к. M-sup{X}=> 1 из верхних граней, то по определению для х из Х=> х< =М, а значит он не может быть > M => x не из Х
2. Берем С< M. Пусть нету х, удовлетвор. 2му свойству=> для всякого х< =с, а это значит, что С есть М и при этом С< М, а значит М не есть sup{X}, что противоречит условию=> x> c
2. Достаточность. Дано: 1, 2. Доказать: что М=sup{X}. Док-во.
1. Из 1пункта следует, что М есть верхняя грань{X}, (x> M=> х не их Х=> любое х из Х меньше М)
2. Из пункта 2 есть х> с=> с ни есть верхняя грань=> М наименьшая из всех верхних граней.
В2. Абсолютная величина и ее свойства.
Модуль числа x - это найбольшее из {+x и -x}. Так же модулем числа x называется само число x, если x> =0 и –x при x< 0
Свойства
1)|x|> =0 из определения(|x|=max{x, -x})
2)-|x|< =x< =|x|
a)x=0 -0=0=0
б)x< 0 x=-|x| |x|=-x -|x|=x< |x|
в)x> 0 -|x|< x=|x|
3)если a> =0, |x|< =aó -a< =x< =a
x> 0, |x|=x x(> =0)< =a -a(< =0)< =x(> =0) => -a< =x< =a
x< 0, |x|=-x a(< 0)> -x(> 0) x< =a a> =x> =-a
4) |x+y|< =|x|+|y|
-|x|< =x< =|x| |x|=max{x, -x}
-|y|< = y< =|y| |x|=max{x, -x}
-(|x|+|y|)(это -а)< =x+y< =(|x|+|y|)(это а) –max{x, -x}=-|x|
x> =-max{x, -x} |x-y|< =|x|+|y|
5. |x-y|> =||x|-|y||
|x|=|x-y+y|< =|x-y|+|y| |x-y|> =|x|-|y| |y|=|y-x+x|< =|y-x|+|x|=|x-y|+|y| |x-y|> =|y|-|x| |x-y|> =|y|-|x| |x-y|> =max{|x|-|y|, |y|-|x|}
6. |x*y|=|x||y|
3. Определение функции, способы ее задания. Функции четные и нечетные
Функция - это зависимость одной величины от другой.
Если существует взаимооднозначное соответствие между переменной х одного множества и переменной у другого множества, то она называется функциональной зависимостью. y=f(x).
Определение способа задания:
-аналитически (y=kx+b)
-графический (график)
-таблично
| x | |||
| y |
-алгоритмически (с помощью ЭВМ)
Классификация функций:
Чётная функция, функция, удовлетворяющая равенству f(-х)=f(x) при всех х.
Нечётная функция, функция, удовлетворяющая равенству f (-x) = -f (x).
Монотонная функция функция, которая при возрастании аргумента либо всегда возрастает (или хотя бы не убывает), либо всегда убывает (не возрастает).
Определение f(x) монотонности: Пусть Х принадлежит области определение D ( ]xÌ D)
Пусть Х подмножество в области определения в f(x).
Функция у=f(x) называется:
1) Возрастающая на Х, если для любого х1; х2 принадлежащие Х: х1< x2Þ f(x1)< f(x2)
2) Убывающий на Х, если для любого х1; х2 принадлежащие Х: х1< x2Þ f(x1)> f(x2)
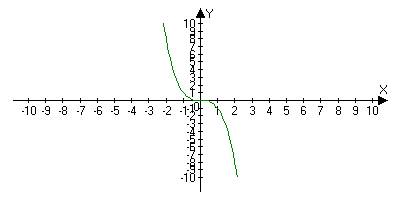
3) Не убывающий на Х, если для любого х1; х2 принадлежащие Х: х1< x2Þ f(x1)£ f(x2)
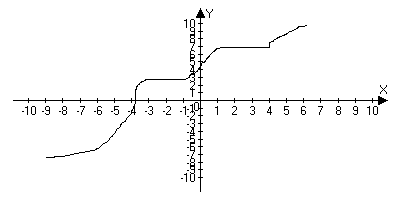
4 Не возрастающая на Х, если для любого х1; х2 принадлежащие Х: х1< x2Þ f(x1)³ f(x2)
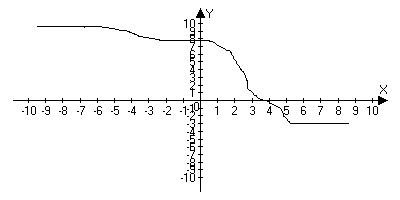
Определение:
Ограниченность. Пусть Х включает D y=f(x) называется:
1) Ограниченной сверху на Х если существует В, так что для любого х принадлежащего Х выполняется x£ R
2) Ограниченной снизу на Х если существует А, так что для любого х принадлежащего Х выполняется А£ х
3) Ограниченной и сверху и снизу на Х если существует А, В, так что для любого х принадлежащего Х выполняется А£ х£ В, или существует С, так что для любого х принадлежащего Х выполняется |х|£ С
Обратная функция, функция, обращающая зависимость, выражаемую данной функцией. Так, если у = f(x) — данная функция, то переменная х, рассматриваемая как функция переменной у: х = ((у), является обратной по отношению к данной функции у = f(x). Например, х = есть О. ф. по отношению к у = х3.
Определение (обратной функции):
Пусть существует D, E, C, R
На D: y=f(x) с областью значений Е. Если для каждого у из y=f(x) найдётся единственный х, то говорят, что на множестве Е задана функция обратная к функции f(x), с областью значений D. Иными словами две функции y=f(x) и x=g(y) являются взаимно обратными если выполняется тождества:
 | 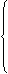 |
y=f(g(y)), " yÎ E y=f(g(y)), для любого уÎ Е
Û
x=g(f(x)), " xÎ D x=g(f(x)), для любого хÎ D
Примеры:
1)y=x3 Û x=3Ö y
D=R
E=R
Элементарные: - функции, которые получаются из основных элементарных ф-ций с помощью алгебраических действий (+, -, *, /, введение в степень). Основные элементарные ф-ции:
1. y=xn - степенная
2. y=ax - показательная
3. y=logax - логарифмическая
4. y=sinx, y=cosx - тригонометрические.
5. y=c где c -постоянная
Сложные:
Y=f(U), где U=j(x), Y=f[j(x)]
Если ф-ция у зависит от промежуточного аргумента U, который зависит от независимой переменной х, то y=f[j(x)] называется сложным заданием х.
Пусть задано D, E, G, C, R
На D: y=f(x) с областью значения E
На E: z=g(y) с областью значения G
Тогда на множестве D определена сложная функция z=g(f(x)) с областью значения G. Тогда говорят, что g(f(x)) есть суперпозиция функций g, f.
Пример: Пример
z=sin ex w=arctgcos exx-ln x
y=ex=f(x)
z=sin y=g(y)
D=R
E=R+
G=[-1; 1]
4. Предел функции и его единственность. Бесконечно малые и их свойства. Связь предела с бесконечно малыми.
Число А называется пределом ф-ции f(x) при х®x0, если для каждого, как угодно малого на период заданного числа e. -e> 0, найдется такое как угодно малое на период заданного d> 0, что будут выполняться неравенства: Если 0< |x-x0|< d, то |f(x)-A|< e и х! =х0
Основные св-ва:
1. Если величина имеет предел, то только 1.
Док-во
{xn} имеет два разл. Предела a и b, а¹ b. Тогда согласно определению пределов любая из окрестностей т. а содержит все эл-ты посл-ти xn за исключением конечного числа и аналогичным св-вом обладает любая окрестность в точке b. Возьмем два радиуса e = (b-a)/2, т. к. эти окрестности не пересекаются, то одновременно они не могут содержать все эл-ты начиная с некоторого номера. Получим противоречие теор. док-на.
2. limC=C, где С- постоянная величина
Св-ва б. м. в.:
Если a-б. м. в., то lima=0
Это по определению(d(x) –называется БМВ в точке х0, если lin d(x)=0 при x-> x0)
1. Если 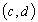 и
и 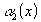 - бесконечно малые при
- бесконечно малые при  , то сумма
, то сумма 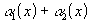 - тоже бесконечно малая при
- тоже бесконечно малая при  ;
;
2. Если 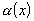 - бесконечно малая и
- бесконечно малая и 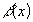 - ограниченная при
- ограниченная при  , то произведение
, то произведение 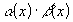 есть бесконечно малая при
есть бесконечно малая при  .
.
3. Если 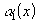 и
и 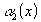 - бесконечно малые при
- бесконечно малые при  , то произведение
, то произведение 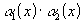 - тоже бесконечно малая при
- тоже бесконечно малая при  ;
;
Доказательство
1. В качестве 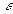 выберем такое число
выберем такое число 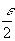 , что
, что
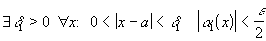
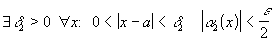
Обозначив 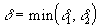 , получаем:
, получаем:
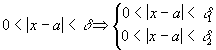
 .
.
По свойству модулей: 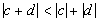 , обозначив
, обозначив 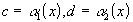 получаем:
получаем: 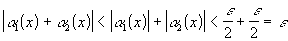 . Таким образом,
. Таким образом, 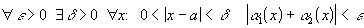 , т. е.
, т. е. 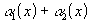 - бесконечно малая.
- бесконечно малая.
2. 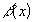 - ограничена при
- ограничена при  , т. е.
, т. е. 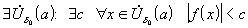 .
.
Тогда в качестве 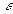 можно выбрать число
можно выбрать число 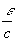 . Тогда
. Тогда 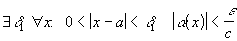 .
.
Обозначив за  получаем:
получаем: 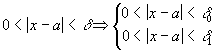
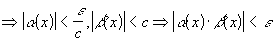 . Значит,
. Значит,  , т. е.
, т. е. 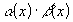 - бесконечно малая при
- бесконечно малая при  .
.
3. Докажем лемму. Если  - бесконечно малая при
- бесконечно малая при  , то она ограничена при
, то она ограничена при  . (наоборот - неверно! ). Доказательство: возьмем
. (наоборот - неверно! ). Доказательство: возьмем 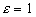 и получим, что
и получим, что 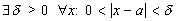
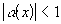 . Таким образом, при
. Таким образом, при 
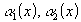 - бесконечно малые. По доказанной лемме
- бесконечно малые. По доказанной лемме 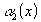 - ограничена. Следовательно, по свойству 2 данной теоремы
- ограничена. Следовательно, по свойству 2 данной теоремы 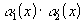 - бесконечно малая.
- бесконечно малая.
Cвязь предела и БМВ
Теорема Для того, чтобы f(x) имела конечный предел в х0. Необходимо и достаточно, чтобы она была представима: f(x)= a+A(x), где A(х)- БМВ в х0 a=Lim f(x) при x-> x0
Док-во: 1. Необходимость. есть хотябы 1 a=Lim f(x) x-> 0 Доказать: f(x)=a+A(x)Док-во.
Обозначим A(X)=f(x)-a и любое E> 0 есть хотябы 1 D> 0 тогда, любое х: 0< |x-x0|< D => |f(x)-a|=A(x)< E чтд
2. Достаточность. Есть f(x)=a+A(x) Доказать a=LimF(x) при х-> x0 Док-во
| любое E> 0 есть хотябы 1 D> 0 тогда, любое х: 0< |x-x0|< D => |f(x)-a|=|A(x)|< E чтд
В5. Неограниченные величины. Бесконечно большие и их связь с БМВ.
Неограниченной величиной(НВ)-g(x) неограниченна в х0, если любое М> 0 и любое D> 0 есть хотябы 1 х: 0< |x-x0|< D => |g(x)|> M
График- правая ветвь параболы.
g(x) -, бесконечно большая в х0, если Lim(g(x))=беск x-> x0
Всякая ББВ величина неограничена
Св-ва:
-величина обратная б. б. в. явл. б. м. в. (1/¥ =0; 1/0=¥ )
Док-во Пусть f(x) ББВ, то, если любое E> 0 и любое D> 0 есть хотябы 1 х: 0< |x-x0|< E => f(x) > 1/E=> |1/f(x)|< E
-сумма б. б. в. (с одинаковым знаком) есть б. б. в.
-произведение 2х б. м. величин=б. м. в.
-частное от деления 2х б. б. в = неопределенность
В6. Предел последовательности. Ограниченность последовательности, имеющей предел. Предел монотонной функции.
Последовательность- функция целочисленного аргумента.
Предел последовательности:
y=f(Un), где U1, U2,... Un, а Un=n/(n2+1)
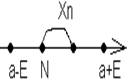 Предел: число а называется пределом переменной xn, если для каждого “+” как угодно малого числа e(эпсилон) существует такой номер N, что при n> N разность |xn-a|< e
Предел: число а называется пределом переменной xn, если для каждого “+” как угодно малого числа e(эпсилон) существует такой номер N, что при n> N разность |xn-a|< e
limxn=a
n®¥ -e< Xn-a< e a-e< Xn< a+e
Если последовательность монотонно возрастает и ограниченна сверху, то она имеет предел.
Последовательность монотонно возрастает, если последующий член> предыдущего (xn+1> xn)
Последовательность ограничена сверху, если существует такое М, что xn< =M.
Ограниченность последовательности, имеющей конечный предел.
Lim an=a n-> беск возмем m и M любое n => m< =an< =M любое E> 0 есть хоть 1 N любое n> N=> |an-a|< E=> -E< an-a< E=> a-E< an< a+E m1-min из послед an M-max из послед an m=min{m1, a-E} M=max{M1, a+E} m< an< M чтд
Функция 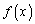 монотонно возрастающей, если из
монотонно возрастающей, если из 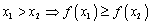 -строго монотонно возрастающей, если из
-строго монотонно возрастающей, если из 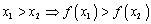 - монотонно убывающей, если из
- монотонно убывающей, если из 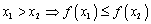 -строго монотонно убывающей, если из
-строго монотонно убывающей, если из 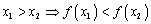 . Докажем одну из возможных здесь теорем. Теорема. Если
. Докажем одну из возможных здесь теорем. Теорема. Если 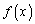 монотонно возрастает и ограниченна сверху при
монотонно возрастает и ограниченна сверху при 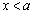 , то существует конечный предел слева
, то существует конечный предел слева 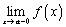 . Доказательство. Рассмотрим множество
. Доказательство. Рассмотрим множество 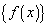 значений функции
значений функции 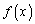 при
при 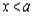 . По условию теоремы, это множество ограниченно сверху, т. е.
. По условию теоремы, это множество ограниченно сверху, т. е. 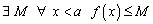 . По теореме о существовании супремума(1. Если последовательность
. По теореме о существовании супремума(1. Если последовательность 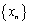 монотонно возрастает и ограниченна сверху, то она сходится к конечному пределу; 2. Если последовательность
монотонно возрастает и ограниченна сверху, то она сходится к конечному пределу; 2. Если последовательность 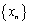 монотонно возрастает, но неограниченна сверху, то
монотонно возрастает, но неограниченна сверху, то 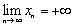 . ) отсюда следует, что существует конечный
. ) отсюда следует, что существует конечный 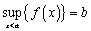 . Покажем, что
. Покажем, что 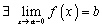 . По свойствам супремума 1.
. По свойствам супремума 1. 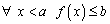 2.
2. 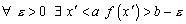 Обозначим
Обозначим 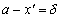 . Возьмем любое x, для которого
. Возьмем любое x, для которого 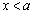 , но
, но 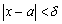 . Как видно из рисунка, из этого следует, что
. Как видно из рисунка, из этого следует, что 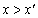 . Но тогда, в силу монотонности
. Но тогда, в силу монотонности 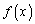 а)
а) 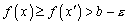 б)
б) 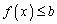 Поэтому имеем
Поэтому имеем 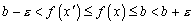 Выбрасывая лишнее получим, что
Выбрасывая лишнее получим, что 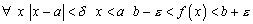 или, что то же самое,
или, что то же самое, 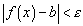 . По определению предела функции это означает, что
. По определению предела функции это означает, что 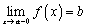 .
.
В7. Предельный переход в равенствах в неравенства. Теорема о “двух милиционерах. ”
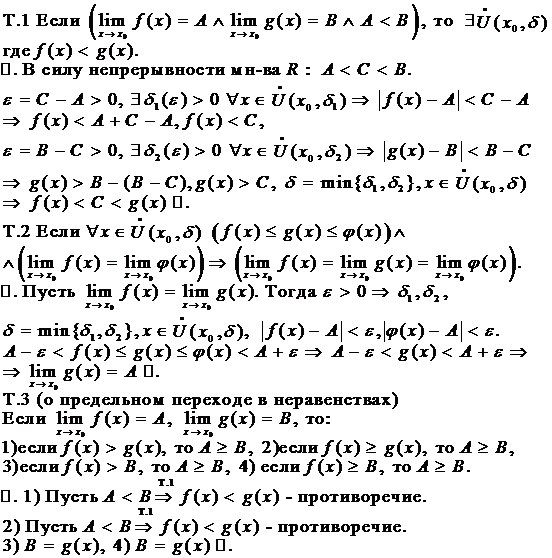
Теорема. Пусть во всех точках некого мн-ва f(x)< =g(x) и при этом есть конечные пределы, тогда a< b…. f(x)< =g(x) Lim f(x)=a Lim g(x)=b при x-> x0 получаем a< =b.
Док-во. Пусть a> b и E=(a-b)/4 есть хоть1 D1 и любой х: |x-x0|-D1=> |f(x)-a|< E=(a-b)/4=> -(a-b)/4< f(x)-a< (a-b)/4 (3a+b)/4< f(x)< (5a-b)/4
есть хоть1 D2 и любой х: 0< |x-x0|< D1=> |g(x)-b|< E=(a-b)/4
Теорема о “двух милиционерах”: Пусть нам заданы 3 функции на определенном промежутке, связанные следующим образом f(x)< =g(x)< =h(x) и еще выполняется Lim f(x)=a Lim h(x)=a при x-> x0, то получаем, что Lim g(x)=a при x-> x0.
Док-во: берем E1 и D1 для h хоть одно E> 0 любое D> 0 любое х: 0< |x-x0|< D => |f(x)-a|< D и |h(x)-a| < D => -D< f(x)-a< D -D< h(x)-a< D a-D< f(x)< D+a a-D< h(x)< D+a a-D< f(x)< =g(x)< =h(x)< a+D a-D< g(x)< a+D => |g(x)-a|< E
В8. Первый замечательный предел.
Терема lim (sin(x)/x)=1
x®0
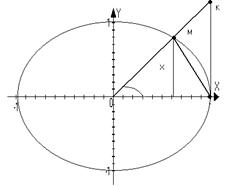 Доказательство:
Доказательство:
S∆ OMN=1/2 sin(x)
SсекOMN=1/2(x)
S∆ OKN=1/2 tg(x)
S∆ OMN< SсекOMN< S∆ OKN
1/2sin(x)< 1/2(x)< tg(x)
sin(x)< x< tg(x)
1< x/sin(x)< 1/cos(x)
lim (1-cos(1/n))=0
n®+¥
lim (1-cos(x))=0 Þ lim (cos(x))=1
x®0 x®0
lim (x/sin(x))=0
x®0
x> 0 lim (x/sin(x))=1
x®0
lim(1/(x/sin(x)))= lim(sin(x)/x)=1 что и требовалось доказать
x®0 x®0
В8. Первый замечательный передел
Первым замечательным пределом называется предел
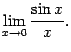
Теорема 2. 14 Первый замечательный предел равен 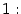
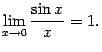
Доказательство. Рассмотрим два односторонних предела 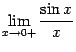 и
и 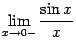 и докажем, что каждый из них равен 1. Тогда по теореме 2. 1 двусторонний предел
и докажем, что каждый из них равен 1. Тогда по теореме 2. 1 двусторонний предел 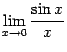 также будет равняться 1.
также будет равняться 1.
Итак, пусть 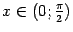 (этот интервал -- одно из окончаний базы
(этот интервал -- одно из окончаний базы 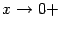 ). В тригонометрическом круге (радиуса
). В тригонометрическом круге (радиуса  ) с центром
) с центром  построим центральный угол, равный
построим центральный угол, равный 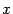 , и проведём вертикальную касательную в точке
, и проведём вертикальную касательную в точке 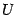 пересечения горизонтальной оси с окружностью (
пересечения горизонтальной оси с окружностью ( 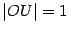 ). Обозначим точку пересечения луча с углом наклона
). Обозначим точку пересечения луча с углом наклона 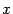 с окружностью буквой
с окружностью буквой 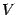 , а с вертикальной касательной -- буквой
, а с вертикальной касательной -- буквой 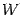 ; через
; через 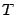 обозначим проекцию точки
обозначим проекцию точки 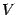 на горизонтальную ось.
на горизонтальную ось.
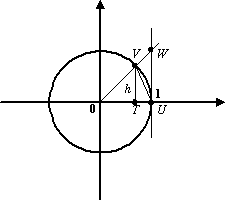
Рис. 2. 27. Тригонометрический круг
Пусть 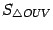 -- площадь треугольника
-- площадь треугольника 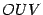 ,
, 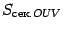 -- площадь кругового сектора
-- площадь кругового сектора 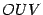 , а
, а 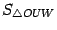 -- площадь треугольника
-- площадь треугольника 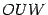 . Тогда очевидно следующее неравенство:
. Тогда очевидно следующее неравенство:
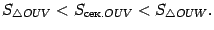
Заметим, что горизонтальная координата точки 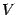 равна
равна 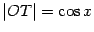 , а вертикальная --
, а вертикальная -- 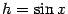 (это высота треугольника
(это высота треугольника 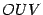 ), так что
), так что 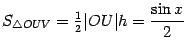 . Площадь центрального сектора круга радиуса
. Площадь центрального сектора круга радиуса 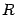 с центральным углом
с центральным углом 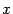 равна
равна 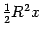 , так что
, так что 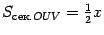 . Из треугольника
. Из треугольника 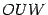 находим, что
находим, что 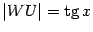 . Поэтому
. Поэтому 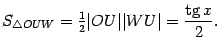 Неравенство, связывающее площади трёх фигур, можно теперь записать в виде
Неравенство, связывающее площади трёх фигур, можно теперь записать в виде
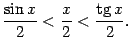
Все три части этого неравенства положительны, поэтому его можно записать так:
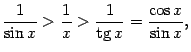
или (умножив на 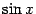 ) так:
) так:
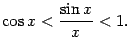
Предел постоянной 1 в правой части неравенства, очевидно, равен 1. Если мы покажем, что при 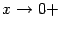 предел
предел 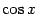 в левой части неравенства тоже равен 1, то по теореме " о двух милиционерах" предел средней части
в левой части неравенства тоже равен 1, то по теореме " о двух милиционерах" предел средней части 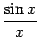 также будет равен 1.
также будет равен 1.
Итак, осталось доказать, что 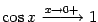 . Сперва заметим, что
. Сперва заметим, что 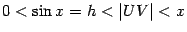 , так как
, так как 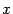 равняется длине дуги окружности
равняется длине дуги окружности 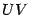 , которая, очевидно, длиннее хорды
, которая, очевидно, длиннее хорды 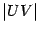 . Применяя теорему " о двух милиционерах" к неравенству
. Применяя теорему " о двух милиционерах" к неравенству
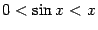
при 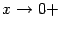 , получаем, что
, получаем, что
|
| (2. 3) |
Простая замена переменной  показывает, что и
показывает, что и 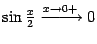 . Теперь заметим, что
. Теперь заметим, что 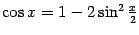 . Применяя теоремы о линейности предела и о пределе произведения, получаем:
. Применяя теоремы о линейности предела и о пределе произведения, получаем:
|
| (2. 4) |
Тем самым показано, что
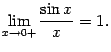
Сделаем теперь замену 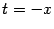 ; при этом база
; при этом база 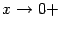 перейдёт в базу
перейдёт в базу 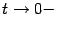 (что означает, что если
(что означает, что если 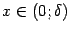 , то
, то 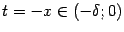 ). Значит,
). Значит,
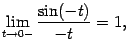
но 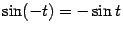 (
( 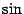 -- нечётная функция), и поэтому
-- нечётная функция), и поэтому 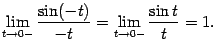 Мы показали, что левосторонний предел также равен 1, что и завершает доказательство теоремы
Мы показали, что левосторонний предел также равен 1, что и завершает доказательство теоремы
В9. Второй замечательный предел
Теорема lim(1+1/x)x=e
x®+¥
Доказательство: Пусть n – целая часть х – n=[x] n£ x< n+1
[1+1/(n+1)]n£ (1+1/x)x£ (1+1/n)n+1
Если x®+¥, то n®+¥
[1+1/(n+1)]n+11/[1+1/(n+1)]£ (1+1/x)x£ (1+1/n)n(1+1/n) Þ lim(1+1/x)x=e
x®+¥
В10. Пределы, связанные со вторым замечательным пределом.
В11. Арифиметические операции над переменными, имеющими предел. Неопределенные случаи.
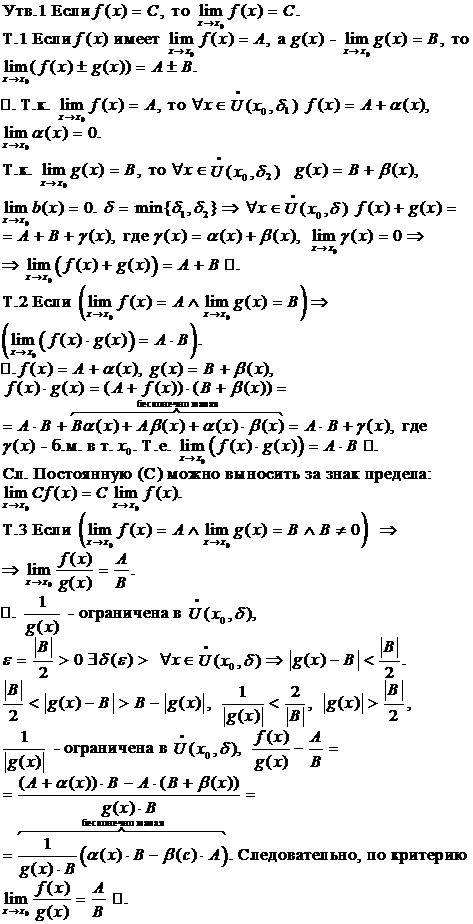
В12. Непрерывность функции в точке и на промежутке. Арифметические операции над непрерывными функциями
Определение: функция f(x) непрерывна, если: 1)она определена в х0 и некоторой ее окресности. 2. Lim f(x)=f(x) при x-> x0
Функция непрерывна на множестве, если она непрерывна в каждой точке этого множества. в качестве примера y=x2.
Арифметические опрерации: f(x)+-/*g(x) если функции непрерывны в х0


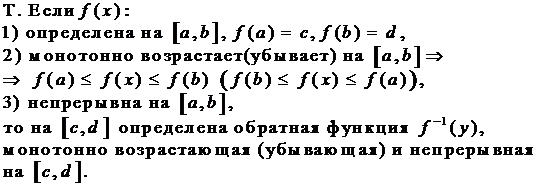
В13. Непрерывность сложной функции. Непрерывность основных элементарных и принадлежащих классу элеменетарных функции.
Пусть функции f(x) и g(x) непрерывны в точке х0. Тогда функция f(x) не равная g(x), f(x)g(x) и (если g(x) не равно 0) непрерывны в точке x0.
Доказательство.
Пусть f(x) и g(x) непрерывны в точке x0. Это значит, что 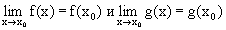 . Но тогда, по свойствам пределов
. Но тогда, по свойствам пределов
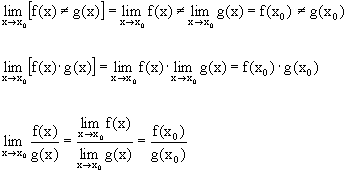
Последнее свойство верно, если 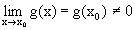 . <
. <
Пусть y=f(x), но x, в свою очередь, является функцией некоторого аргумента t: x=j(t). Тогда комбинация y=f(j(t)) называется сложной функцией, или суперпозицией функции j(t).
Примеры:
а) y=sin(x), x=et => y=sin(et)
б) y= ex, x=sin(t) => y= esin(t)
Целая и дробная рациональные функции. Непрерывность f(x)=const и f(x)=x непосредственно ясна. На основании теоремы о произведении непрерывных функций вытекает непрерывность любого одночленного выражения axm, по теореме о сумме непрерывных функций - непрерывность многочлена a0xn + a1xn-1 +... +an-1 + an. Непрерывность данных функций имеет место на всем интервале  . Частное двух многочленов
. Частное двух многочленов 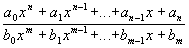 непрерывно всюду, кроме точек b0xm + b1xm-1 +... + bm-1x + bm = 0 (в этих точках - либо разрыв 2-го рода, либо устранимый разрыв).
непрерывно всюду, кроме точек b0xm + b1xm-1 +... + bm-1x + bm = 0 (в этих точках - либо разрыв 2-го рода, либо устранимый разрыв).
Показательная функция y=ax(a> 1) монотонно возрастает на всем интервале  . Ее значения заполняют весь интервал
. Ее значения заполняют весь интервал 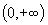 . Из существования логарифма следует непрерывность данной функции.
. Из существования логарифма следует непрерывность данной функции.
Логарифмическая функция 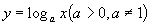 . Рассмотрим случай a> 1. Эта функция возрастает при
. Рассмотрим случай a> 1. Эта функция возрастает при 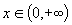 , и принимает любое значение из
, и принимает любое значение из 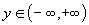 . Отсюда следует ее непрерывность.
. Отсюда следует ее непрерывность.
Степенная функция 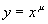 . При возрастании x от 0 до
. При возрастании x от 0 до 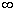 возрастает
возрастает 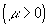 или убывает
или убывает 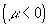 на интервале
на интервале 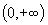 . Следовательно, данная функция непрерывна.
. Следовательно, данная функция непрерывна.
Тригонометрические функции 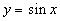 ,
, 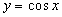 ,
, 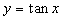 ,
, 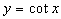 ,
, 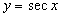 ,
, 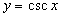 . Остановимся на функции
. Остановимся на функции 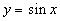 . Ее непрерывность на отрезке
. Ее непрерывность на отрезке 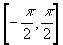 вытекает из ее монотонности, а также из факта (устанавливаемого геометрически), что при этом она принимает все значения от -1 до 1. То же относится к любому промежутку
вытекает из ее монотонности, а также из факта (устанавливаемого геометрически), что при этом она принимает все значения от -1 до 1. То же относится к любому промежутку 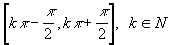 . Следовательно, функция
. Следовательно, функция 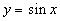 непрерывна для всех значений x. Аналогично - для функции
непрерывна для всех значений x. Аналогично - для функции 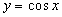 . По свойствам непрерывных функций вытекает непрерывность функций
. По свойствам непрерывных функций вытекает непрерывность функций 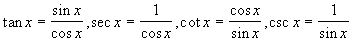 . Исключение для первых двух функций - значения x вида
. Исключение для первых двух функций - значения x вида 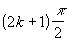 , при которых
, при которых 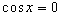 , для других двух - значения вида
, для других двух - значения вида 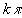 , при которых
, при которых 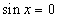 .
.
Обратные тригонометрические функции 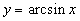 ,
, 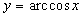 ,
, 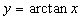 ,
, 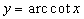 . Первые две непрерывны на
. Первые две непрерывны на 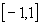 , остальные - на
, остальные - на 
В14. Сравнение и порядок бесконечно малых. Эквиваленты бесконечно малых. Основные примеры
Сравнение бесконечно малых
Определение 2. 16 Пусть фиксирована некоторая база 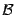 и на некотором её окончании
и на некотором её окончании 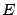 заданы две функции
заданы две функции 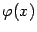 и
и 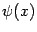 , бесконечно малые при базе
, бесконечно малые при базе 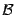 . Предположим также, что
. Предположим также, что 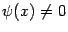 при всех
при всех 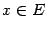 . Пусть существует
. Пусть существует
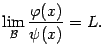
Если 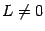 , то бесконечно малая
, то бесконечно малая 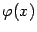 имеет тот же порядок малости, что и
имеет тот же порядок малости, что и 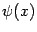 . Этот факт обозначается так:
. Этот факт обозначается так:
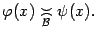
Если же 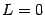 , то
, то 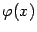 имеет больший порядок малости, чем
имеет больший порядок малости, чем 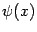 . Это обозначается так:
. Это обозначается так:
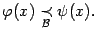 Заметим, что если
Заметим, что если 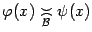 , то для всех
, то для всех 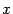 из некоторого окончания
из некоторого окончания 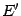 базы
базы 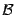 будет выполнено неравенство
будет выполнено неравенство 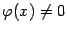 . Это сразу следует из того, что
. Это сразу следует из того, что 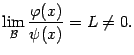
Предложение 2. 2 Если при базе 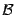 бесконечно малая
бесконечно малая 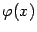 имеет тот же порядок малости, что
имеет тот же порядок малости, что 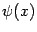 , то и
, то и 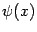 имеет тот же порядок малости, что
имеет тот же порядок малости, что 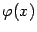 , то есть
, то есть
|
| (S) |
Если две бесконечно малых 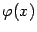 и
и 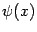 одного порядка малости, и две бесконечно малых
одного порядка малости, и две бесконечно малых 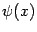 и
и 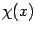 тоже одного порядка малости при базе
тоже одного порядка малости при базе 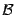 , то две величины
, то две величины 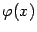 и
и 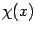 также имеют один и тот же порядок малости при базе
также имеют один и тот же порядок малости при базе 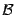 , то есть
, то есть
|
| (T) |
Кроме того, бесконечно малая величина 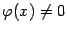 имеет тот же порядок малости, что она же сама:
имеет тот же порядок малости, что она же сама:
|
| (R) |
Доказательство. Поскольку 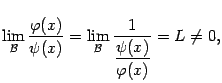 то
то 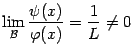 , откуда следует первое из доказываемых утверждений.
, откуда следует первое из доказываемых утверждений.
Второе утверждение следует из первого и цепочки равенств
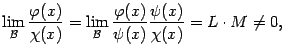
где
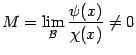
по условию предложения.
Наконец, третье утверждение сразу следует из очевидного соотношения 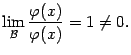
Итак, свойство двух или нескольких бесконечно малых величин иметь один и тот же порядок малости, то есть отношение 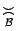 , заданное в множестве бесконечно малых при данной базе
, заданное в множестве бесконечно малых при данной базе 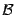 величин
величин 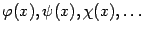 , является рефлексивным, транзитивным и симметричным.
, является рефлексивным, транзитивным и симметричным.
Рефлексивность какого-либо отношения 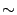 , заданного в некотором множестве объектов
, заданного в некотором множестве объектов 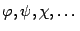 , означает, что выполнено свойство
, означает, что выполнено свойство
(R): 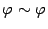 ,
,
транзитивность -- что выполнено свойство
(T): 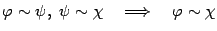 ,
,
а симметричность -- что выполнено свойство
(S): 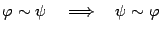 .
.
Любое рефлексивное, транзитивное и симметричное отношение 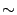 разбивает множество объектов, для которых оно определено, на классы объектов, эквивалентных по данному отношению: в один класс с объектом
разбивает множество объектов, для которых оно определено, на классы объектов, эквивалентных по данному отношению: в один класс с объектом 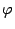 попадают все объекты
попадают все объекты 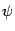 , для которых
, для которых 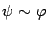 .
.
Поэтому все бесконечно малые при данной базе 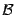 величины разбиваются на классы по отношению
величины разбиваются на классы по отношению 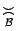 , в каждый из которых входят все величины, имеющие один и тот же порядок малости.
, в каждый из которых входят все величины, имеющие один и тот же порядок малости.
Пример 2. 31 При базе 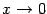 величины
величины 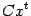 и
и 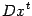 , где
, где 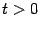 и
и 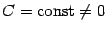 ,
, 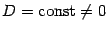 , имеют один и тот же порядок малости (так как, очевидно, их отношение постоянно и его предел
, имеют один и тот же порядок малости (так как, очевидно, их отношение постоянно и его предел 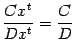 постоянно и его предел равен
постоянно и его предел равен 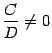 . Например, при
. Например, при 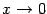 величины
величины 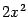 и
и 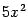 имеют один и тот же порядок малости.
имеют один и тот же порядок малости.
При базе 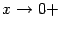 величина
величина 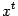 имеет больший порядок малости, чем
имеет больший порядок малости, чем 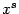 , при
, при 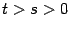 :
:
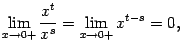
так как 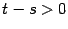 . Если степени
. Если степени 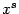 и
и 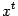 определены и при
определены и при 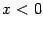 , то аналогичное утверждение верно и для двусторонней базы
, то аналогичное утверждение верно и для двусторонней базы 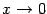 . Например, при
. Например, при 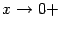 величина
величина 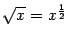 -- большего порядка малости, чем
-- большего порядка малости, чем 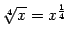 . При
. При 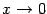 величина
величина  -- большего порядка малости, чем
-- большего порядка малости, чем 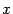 , а
, а 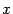 -- величина большего порядка малости, чем
-- величина большего порядка малости, чем 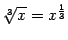 .
.
Пример 2. 34 Поскольку, как мы видели в примерах выше, 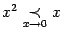 и
и 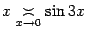 , то
, то  -- величина большего порядка малости, чем
-- величина большего порядка малости, чем 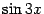 .
.
Определение 2. 17 Пусть 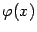 и
и 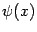 -- бесконечно малые при базе
-- бесконечно малые при базе 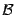 и
и
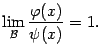
Тогда бесконечно малая 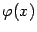 называется эквивалентной бесконечно малой
называется эквивалентной бесконечно малой 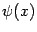 при базе
при базе 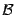 . Это обозначается следующим образом:
. Это обозначается следующим образом:
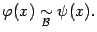
Очевидно, что если величина 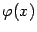 эквивалентна величине
эквивалентна величине 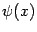 , то они имеют один и тот же порядок малости (так как при этом
, то они имеют один и тот же порядок малости (так как при этом 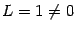 ). Кроме того, свойство двух бесконечно малых величин быть эквивалентными, то есть отношение
). Кроме того, свойство двух бесконечно малых величин быть эквивалентными, то есть отношение 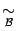 , (так же, как и отношение
, (так же, как и отношение 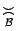 ) рефлексивно, транзитивно и симметрично. А именно, имеет место
) рефлексивно, транзитивно и симметрично. А именно, имеет место
Предложение 2. 4 Если при базе 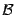 бесконечно малая
бесконечно малая 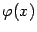 эквивалентна бесконечно малой
эквивалентна бесконечно малой 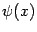 , то и
, то и 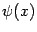 эквивалентна
эквивалентна 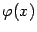 :
:
|
| (S |
Если две бесконечно малых 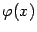 и
и 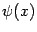 эквивалентны, и две бесконечно малых
эквивалентны, и две бесконечно малых 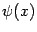 и
и 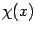 тоже эквивалентны при базе
тоже эквивалентны при базе 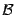 , то две величины
, то две величины 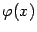 и
и 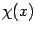 также эквивалентны при базе
также эквивалентны при базе 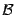 :
:
|
| (T |
Кроме того, величина 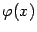 эквивалентна себе самой:
эквивалентна себе самой:
|
| (R |
Доказательствоповторяет доказательство предложения 2. 2. Нужно только учесть, что 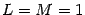 .
.
Итак, отношение эквивалентности 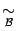 обладает свойствами симметричности (S
обладает свойствами симметричности (S 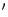 ), транзитивности (T
), транзитивности (T 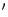 ) и рефлексивности (R
) и рефлексивности (R 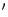 ) и, следовательно, разбивает множество всех бесконечно малых при данной базе
) и, следовательно, разбивает множество всех бесконечно малых при данной базе 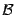 величин на классы эквивалентных между собой бесконечно малых. Эти классы более мелкие, чем классы бесконечно малых величин одного порядка малости, на которые то же самое множество бесконечно малых разбивается отношением
величин на классы эквивалентных между собой бесконечно малых. Эти классы более мелкие, чем классы бесконечно малых величин одного порядка малости, на которые то же самое множество бесконечно малых разбивается отношением 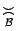 .
.
Пример 2. 35 Согласно первому замечательному пределу, 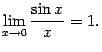 Это означает, что
Это означает, что
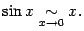
Кроме того, в примере 2. 20 мы показали, что  Это означает, что
Это означает, что
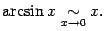
Польза для вычисления пределов от использования эквивалентности бесконечно малых, а также от бесконечно малых большего порядка выражается следующими утверждениями.
Предложение 2. 5 Пусть существует предел 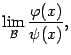 где
где 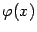 и
и 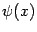 -- бесконечно малые при базе
-- бесконечно малые при базе 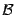 . Пусть также
. Пусть также 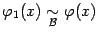 и
и 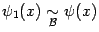 . Тогда существует предел
. Тогда существует предел
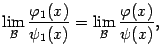
то есть бесконечно малые как в числителе, так и в знаменателе неопределённости вида 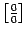 можно заменять на эквивалентные им бесконечно малые: величина предела от этого не изменится.
можно заменять на эквивалентные им бесконечно малые: величина предела от этого не изменится.
Доказательство. Для доказательства напишем такое равенство:
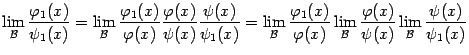
и заметим, что эквивалентность величин 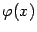 и
и 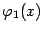 ,
, 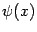 и
и 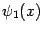 означает, что первый и последний пределы в правой части этой формулы равны 1.
означает, что первый и последний пределы в правой части этой формулы равны 1.
Совершенно так же доказывается уточнение доказанного только что предложения. Это уточнение означает, что заменять эквивалентными можно не только числитель или знаменатель целиком, но и любой бесконечно малый множитель в числителе или знаменателе:
Предложение 2. 6 Пусть 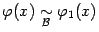 ,
, 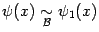 и существует предел
и существует предел
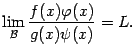
Тогда 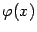 и
и 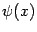 можно заменить на эквивалентные, и значение предела не изменится, то есть
можно заменить на эквивалентные, и значение предела не изменится, то есть
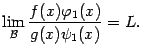
Предложение 2. 7 Пусть 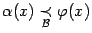 ,
, 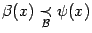 и существует предел
и существует предел  . Тогда существует предел
. Тогда существует предел
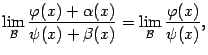
то есть бесконечно малые большего порядка можно отбрасывать как в числителе, так и в знаменателе неопределённости вида 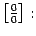 величина предела от этого не изменится.
величина предела от этого не изменится.
Доказательство. Согласно предложению 2. 5, достаточно доказать, что если 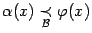 , то
, то 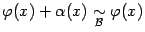 . Но это следует из такой цепочки равенств:
. Но это следует из такой цепочки равенств:
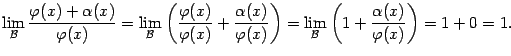
Пример 2. 36 Вычислим предел 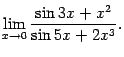
Для этого заметим, что, как мы проверяли выше,  -- величина большего порядка малости, чем
-- величина большего порядка малости, чем 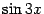 . Аналогично проверяется, что
. Аналогично проверяется, что 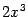 -- величина большего порядка малости, чем
-- величина большего порядка малости, чем 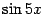 . Поскольку слагаемые большего порядка малости можно отбросить, то
. Поскольку слагаемые большего порядка малости можно отбросить, то
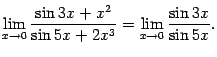
Далее, поскольку 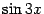 , очевидно, эквивалентен
, очевидно, эквивалентен 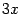 (согласно первому замечательному пределу), а
(согласно первому замечательному пределу), а 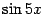 эквивалентен
эквивалентен 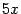 , то последний предел можно упростить, заменив бесконечно малые в числителе и знаменателе на эквивалентные им, а затем сократить на
, то последний предел можно упростить, заменив бесконечно малые в числителе и знаменателе на эквивалентные им, а затем сократить на 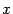 :
:
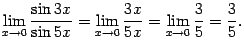
При вычислении пределов часто бывают полезны также следующие два утверждения.
Предложение 2. 8 Пусть 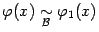 и
и 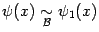 . Тогда:
. Тогда:
1) 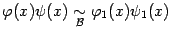
и
2) 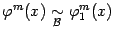 при любом
при любом  (в случае, если степень
(в случае, если степень 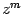 определена только при
определена только при 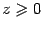 , нужно потребовать, чтобы выполнялось неравенство
, нужно потребовать, чтобы выполнялось неравенство  .
.
(Заметим, что второе утверждение не следует из первого, поскольку 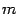 -- не обязательно целое число. )
-- не обязательно целое число. )
Доказательство. Первое утверждение означает, согласно определению эквивалентности, что
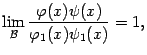
если известно, что
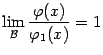
и
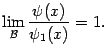
Но это сразу следует из теоремы о пределе произведения ( теорема 2. 9).
Второе утверждение означает, что
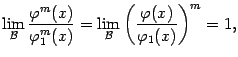
если известно, что
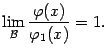
Это следует из того, что степенная функция 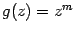 непрерывна при любом
непрерывна при любом 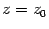 , если
, если  . Как отмечалось выше, для непрерывной функции можно переставлять местами знак функции и знак предела:
. Как отмечалось выше, для непрерывной функции можно переставлять местами знак функции и знак предела:
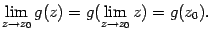
В случае степенной функции 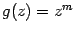 , сделав замену переменного
, сделав замену переменного 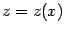 и связанную с ней замену базы, мы получим, что
и связанную с ней замену базы, мы получим, что
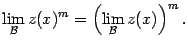
Беря  , получаем, что
, получаем, что
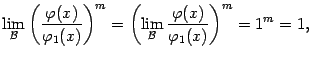
что и требовалось доказать.
Поскольку в этой таблице мы всегда будем рассматривать базу 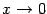 , для простоты записи обозначение этой базы будем пропускать и писать знак
, для простоты записи обозначение этой базы будем пропускать и писать знак 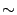 вместо
вместо 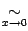 .
.
1) 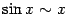 . Эту формулу мы уже доказали и использовали в примерах. Эквивалентность
. Эту формулу мы уже доказали и использовали в примерах. Эквивалентность 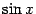 и
и 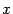 при
при 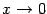 означает в точности, что первый замечательный предел равен 1.
означает в точности, что первый замечательный предел равен 1.
2) 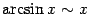 . Эта эквивалентность тоже была доказана выше в одном из примеров.
. Эта эквивалентность тоже была доказана выше в одном из примеров.
3) 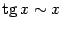 . Докажем эту эквивалентность:
. Докажем эту эквивалентность:
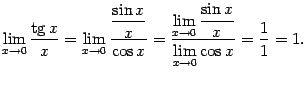
4) 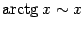 . Докажите это в качестве упражнения, сделав замену
. Докажите это в качестве упражнения, сделав замену 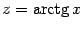 и применив предыдущую табличную формулу.
и применив предыдущую табличную формулу.
5) 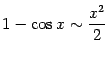 . Для доказательства воспользуемся формулой
. Для доказательства воспользуемся формулой 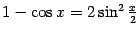 . Далее, имеем:
. Далее, имеем:
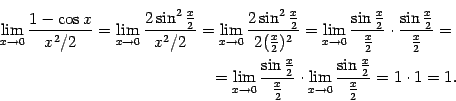
Это означает, что доказываемая эквивалентность имеет место.
6) 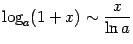 (
( 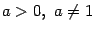 ). Для доказательства этой эквивалентности сделаем такое преобразование:
). Для доказательства этой эквивалентности сделаем такое преобразование:
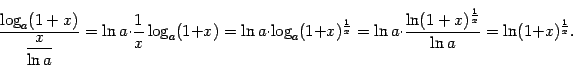
Для вычисления предела правой части воспользуемся непрерывностью логарифма и вторым замечательным пределом:
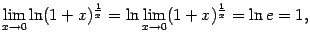
и мы доказали формулу 6.
В частном случае, при 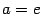 , получаем эквивалентность
, получаем эквивалентность
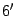 )
) 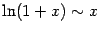 .
.
7) 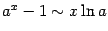 (
( 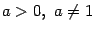 ). Для доказательства сделаем замену
). Для доказательства сделаем замену  и выразим
и выразим 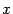 через
через 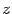 :
: 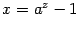 . Согласно формуле 6,
. Согласно формуле 6, 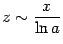 при
при 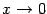 , откуда
, откуда 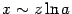 . Из непрерывности логарифма следует, что
. Из непрерывности логарифма следует, что 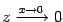 и, значит,
и, значит, 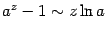 при
при 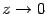 . В этой формуле осталось лишь сменить обозначение переменного
. В этой формуле осталось лишь сменить обозначение переменного 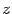 на
на 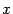 , чтобы получить формулу 7.
, чтобы получить формулу 7.
В частном случае, при 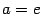 , получаем эквивалентность
, получаем эквивалентность
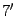 )
) 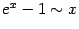 .
.
В15. Сохранение знака непрерывной функции. Понятие равномерной непрерывности.
Напомним, что непрерывность функции 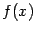 в точке
в точке 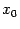 означает, что
означает, что 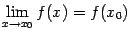 , то есть
, то есть
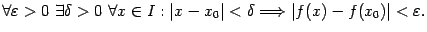
Тем самым непрерывность функции 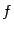 на интервале или отрезке
на интервале или отрезке 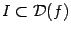 означает, что
означает, что
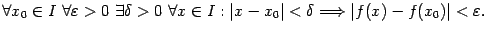
При этом мы имеем право выбирать число 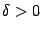 в зависимости от
в зависимости от 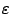 и, главное, от точки
и, главное, от точки 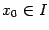 .
.
Предположим теперь, что число 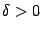 можно выбрать общим для всех
можно выбрать общим для всех 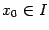 (но, конечно, зависящим от
(но, конечно, зависящим от 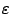 ). Тогда говорят, что свойство функции быть непрерывной в точке
). Тогда говорят, что свойство функции быть непрерывной в точке 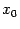 выполнено равномерно по
выполнено равномерно по 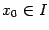 .
.
Дадим теперь такое
Определение 3. 5 Пусть 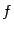 -- некоторая функция и
-- некоторая функция и 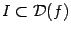 . Функция
. Функция 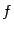 равномерно непрерывна на
равномерно непрерывна на 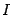 , если
, если
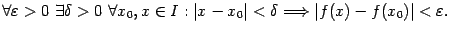
Приведём пример равномерно непрерывной функции.
Пример 3. 15 Рассмотрим функцию 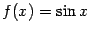 и покажем, что она равномерно непрерывна на всей числовой оси
и покажем, что она равномерно непрерывна на всей числовой оси 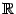 . Фиксируем число
. Фиксируем число 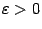 и положим
и положим 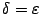 . Выберем теперь любые две точки
. Выберем теперь любые две точки 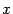 и
и 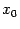 , такие что
, такие что 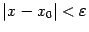 , и покажем, что тогда
, и покажем, что тогда 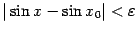 . Действительно,
. Действительно,
|
|
|
так как, во-первых, 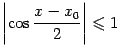 при всех
при всех 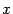 и
и 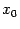 и, во-вторых,
и, во-вторых, 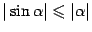 при всех
при всех 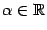 (у нас
(у нас 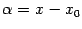 ). Таким образом. равномерная непрерывность функции
). Таким образом. равномерная непрерывность функции 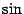 доказана.
доказана.
Лучше изучить условие равномерности по 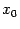 мы сможем, приведя пример, где оно нарушается.
мы сможем, приведя пример, где оно нарушается.
Пример 3. 16 Пусть функция  рассматривается на интервале
рассматривается на интервале 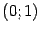 . Если фиксирована точка
. Если фиксирована точка 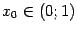 , то для заданного
, то для заданного 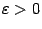 мы можем выбрать
мы можем выбрать 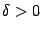 так, что
так, что 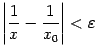 при всех
при всех 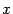 таких, что
таких, что 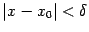 ; для нахождения
; для нахождения 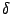 нужно решить неравенство
нужно решить неравенство 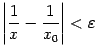 относительно
относительно 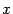 (напомним, что точка
(напомним, что точка 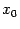 фиксирована):
фиксирована):
|
|
|
|
|
|
Из чисел 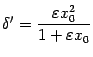 и
и 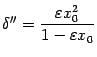 выберем минимальное:
выберем минимальное:
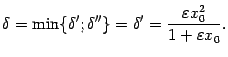
Тогда при 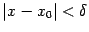 будет
будет 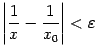 . Проанализируем, однако, зависимость
. Проанализируем, однако, зависимость 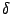 от
от 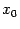 : при
: при 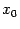 , приближающемся к 0, значения
, приближающемся к 0, значения 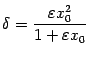 будут убывать и стремиться к 0 (при неизменном значении
будут убывать и стремиться к 0 (при неизменном значении 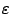 ), что хорошо видно на следующем чертеже:
), что хорошо видно на следующем чертеже:
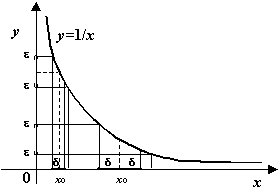
Рис. 3. 25. Изменение 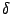 в зависимости от положения точки
в зависимости от положения точки 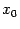
При приближении точки 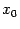 к началу координат нам приходится по одному и тому же
к началу координат нам приходится по одному и тому же 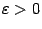 выбирать всё меньшие
выбирать всё меньшие 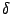 -окрестности точки
-окрестности точки 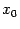 , чтобы обеспечить выполнение неравенства
, чтобы обеспечить выполнение неравенства 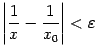 . Выбрать
. Выбрать 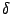 общим для всех
общим для всех 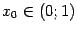 , очевидно, невозможно: при заданном
, очевидно, невозможно: при заданном 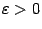 какое бы фиксированное число
какое бы фиксированное число 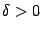 ни было взято, мы можем поместить точку
ни было взято, мы можем поместить точку 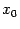 так близко от 0, что значения
так близко от 0, что значения 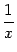 и
и 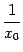 будут отличаться друг от друга больше, чем на
будут отличаться друг от друга больше, чем на 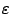 , хотя
, хотя 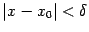 . Это означает, что функция
. Это означает, что функция  не является равномерно непрерывной на интервале
не является равномерно непрерывной на интервале 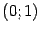 .
.
Теорема 3. 10 Пусть 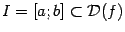 и функция
и функция 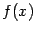 непрерывна на
непрерывна на 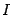 . Тогда
. Тогда 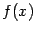 равномерно непрерывна на
равномерно непрерывна на 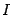 .
.
Доказательство этой теоремы достаточно сложно и основывается на тонких свойствах системы действительных чисел, а именно, на том, что любой замкнутый отрезок 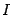 является компактом9. Мы пропускаем здесь доказательство теоремы, отсылая за ним заинтересованного читателя к подробным курсам математического анализа, например, Никольский С. М., Курс математического анализа, т. 1. -- М.: Наука, 1991; Фихтенгольц Г. М., Курс дифференциального и интегрального исчисления, т. 1. -- М. -Л.: ГИТТЛ, 1948 и др. годы изд.
является компактом9. Мы пропускаем здесь доказательство теоремы, отсылая за ним заинтересованного читателя к подробным курсам математического анализа, например, Никольский С. М., Курс математического анализа, т. 1. -- М.: Наука, 1991; Фихтенгольц Г. М., Курс дифференциального и интегрального исчисления, т. 1. -- М. -Л.: ГИТТЛ, 1948 и др. годы изд.
В качестве следствия равномерной непрерывности легко получается утверждение теоремы 3. 8, а именно,
Следствие 3. 1 Любая функция 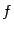 , непрерывная на замкнутом отрезке
, непрерывная на замкнутом отрезке 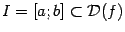 , ограничена на
, ограничена на 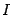 (то есть существует такое число
(то есть существует такое число 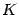 , что
, что 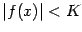 при всех
при всех 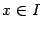 ).
).
Приведём это доказательство (хотя теорема 3. 8 была ранее доказана другим способом):
Доказательство. Фиксируем какое-либо число 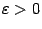 , например
, например 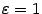 , и выберем
, и выберем 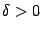 такое, что при всех
такое, что при всех 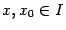 , для которых
, для которых 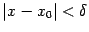 , будет
, будет 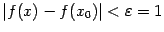 . Разобьём
. Разобьём 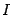 на отрезки длины
на отрезки длины 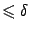 :
:
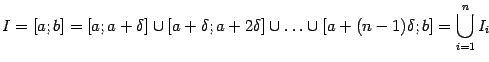
(мы положили 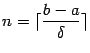 ; 10 длина последнего отрезка может оказаться меньше
; 10 длина последнего отрезка может оказаться меньше 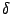 ). Выберем в качестве
). Выберем в качестве 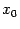 середину
середину 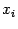 каждого из отрезков:
каждого из отрезков:
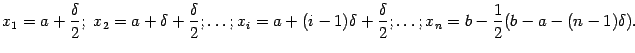
Тогда для каждого 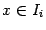 выполняется неравенство
выполняется неравенство 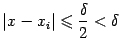 и, следовательно,
и, следовательно, 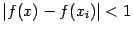 . Это неравенство эквивалентно такому:
. Это неравенство эквивалентно такому:  , или
, или 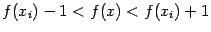 . Поскольку точек
. Поскольку точек 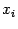 конечное число (а именно,
конечное число (а именно, 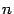 ), то мы можем взять минимальное из чисел
), то мы можем взять минимальное из чисел 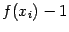 ,
, 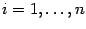 , и максимальное из чисел
, и максимальное из чисел 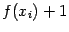 ,
, 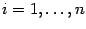 :
:
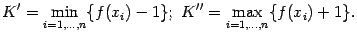
Тогда для любого 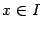 верно неравенство
верно неравенство 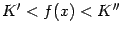 , и осталось взять
, и осталось взять 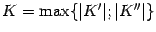 . При этом для любого
. При этом для любого 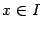 будет
будет 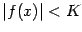 , что означает ограниченность функции
, что означает ограниченность функции 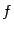 на
на 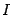 .
.
Теорема кантора Если функция непрерывна на [a, b], то она равномерно непрерывна на [a, b].
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|