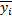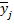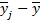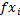- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Расчетное задание. 1 этап. Корреляционный анализ. Сумма по столбцам. Сумма по столбцам
Министерство образования России
Липецкий государственный технический университет
Кафедра управления автотранспортом
Расчетное задание
«Исследование зависимости коэффициента технической готовности от возраста автомобиля»
Вариант №3
Выполнил: студент гр. ДД-09
Кобзева В. О.
Проверил: Гринченко А. В.
Липецк - 2012
Коэффициент технической готовности парка автомобилей (фактор y) – отношение количества технически исправных автомобилей к общему количеству автомобилей в парке.
Возраст автомобиля – фактор x.
Исходные данные:
N=60 – объем выборки.
Таблица 1
| yj | xi лет | yj | xi лет | yj | xi лет | yj | xi лет | yj | xi лет |
| 0, 6 | 0, 65 | 0, 9 | 0, 68 | 0, 91 | |||||
| 0, 55 | 0, 81 | 0, 96 | 0, 55 | 0, 81 | |||||
| 0, 95 | 0, 67 | 0, 69 | 0, 69 | 0, 89 | |||||
| 0, 96 | 0, 77 | 0, 86 | 0, 86 | 0, 72 | |||||
| 0, 6 | 0, 65 | 0, 68 | 0, 68 | 0, 91 | |||||
| 0, 63 | 0, 91 | 0, 55 | 0, 7 | 0, 52 | |||||
| 0, 8 | 0, 92 | 0, 7 | 0, 89 | 0, 6 | |||||
| 0, 87 | 0, 99 | 0, 89 | 0, 8 | 0, 91 | |||||
| 0, 59 | 0, 87 | 0, 96 | 0, 9 | 0, 82 | |||||
| 0, 69 | 0, 7 | 0, 69 | 0, 78 | 0, 83 | |||||
| 0, 6 | 0, 65 | 0, 95 | 0, 68 | 0, 91 | |||||
| 0, 55 | 0, 81 | 0, 98 | 0, 55 | 0, 81 |
1 этап. Корреляционный анализ
Корреляционный анализ позволяет установить наличие и степень выраженности зависимости между факторами y и x.
Разобьем значение факторов x и y на интервалы. Фактор y округлим до сотых, x – до целых.
Величины интервалов вычислим по формулам:
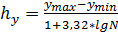 ;
; 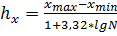
| ymin | ymax | xmin | xmax |
|
0, 52 |
0, 99 |
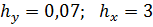
Полученные интервалы внесем в таблицу.
Корреляционная таблица.
Таблица 2
| Границы | Середины | Границы интервалов yj | fxi |
| ||||||
| [0, 52; 0, 59) | [0, 59; 0, 66) | [0, 66; 0, 73) | [0, 73; 0, 8) | [0, 8; 0, 87) | [0, 87; 0, 94) | [0, 94; 1, 01) | ||||
| Середины интервалов yj | ||||||||||
| 0, 555 | 0, 625 | 0, 695 | 0, 765 | 0, 835 | 0, 905 | 0, 975 | ||||
| [2; 5) | 3, 5 |
|
|
|
0, 85 | |||||
| [5; 8) | 6, 5 |
|
|
|
0, 86 | |||||
| [8; 11) | 9, 5 |
0, 77 | ||||||||
| [11; 14) | 12, 5 |
|
|
|
|
|
0, 64 | |||
| [14; 17) | 15, 5 |
|
|
|
|
0, 64 | ||||
| [17; 20) | 18, 5 |
|
|
|
|
|
0, 80 | |||
| [20; 23) | 21, 5 |
|
|
|
|
|
|
0, 56 | ||
| [23; 26) | 24, 5 |
|
|
|
|
|
0, 59 | |||
| fyj |
|
| ||||||||
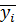 – среднее значение функции отклика i-того интервала.
– среднее значение функции отклика i-того интервала.
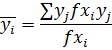
Таблица 3
| xi | fxi | xi2 | xi fxi | xi2 fxi | ∑ yj fxi yj | ∑ xi yj fxi yj |
| 3, 5 | 12, 25 | 38, 5 | 134, 75 | 9, 395 | 32, 8825 | |
| 6, 5 | 42, 25 | 13, 78 | 89, 57 | |||
| 9, 5 | 90, 25 | 12, 38 | 117, 61 | |||
| 12, 5 | 156, 25 | 62, 5 | 781, 25 | 3, 195 | 39, 9375 | |
| 15, 5 | 240, 25 | 1441, 5 | 3, 82 | 59, 21 | ||
| 18, 5 | 342, 25 | 684, 5 | 1, 6 | 29, 6 | ||
| 21, 5 | 462, 25 | 924, 5 | 1, 11 | 23, 865 | ||
| 24, 5 | 600, 25 | 1200, 5 | 1, 18 | 28, 91 | ||
|
Сумма по столбцам |
421, 585 | |||||
Таблица 4
| yj | fyj | yj2 | yj fyj | yj2 fyj |
| 0, 555 | 0, 308 | 3, 33 | 1, 848 | |
| 0, 625 | 0, 391 | 5, 625 | 3, 516 | |
| 0, 695 | 0, 483 | 9, 035 | 6, 279 | |
| 0, 765 | 0, 585 | 1, 53 | 1, 170 | |
| 0, 835 | 0, 697 | 8, 35 | 6, 972 | |
| 0, 905 | 0, 819 | 11, 765 | 10, 647 | |
| 0, 975 | 0, 951 | 6, 825 | 6, 654 | |
|
Сумма по столбцам |
46, 46 |
37, 088 | ||
Среднее значение функции отклика
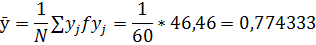
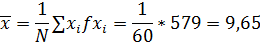
Среднее значение квадрата функции отклика

Общая дисперсия
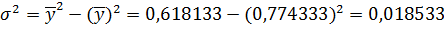
Таблица 5
|
|
|
|
|
| 0, 85 | 0, 079758 | 0, 069975 | |
| 0, 86 | 0, 086917 | 0, 120873 | |
| 0, 77 | -0, 000583 | 0, 000005 | |
| 0, 64 | -0, 135333 | 0, 091575 | |
| 0, 64 | -0, 137666 | 0, 113712 | |
| 0, 80 | 0, 025667 | 0, 001318 | |
| 0, 56 | -0, 219333 | 0, 096214 | |
| 0, 59 | -0, 184333 | 0, 067957 | |
|
Сумма |
0, 561629 | ||
Межинтервальная дисперсия
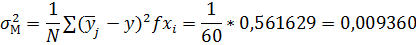
Эмпирическое корреляционное отношение (η ) позволяет установить степень выраженности зависимости между факторами x и y. Может принимать значения от 0 до 1.
0, 9< η < 1 – ярко выраженная зависимость;
0, 85< η < 0, 9 – выраженная зависимость;
0, 75< η < 0, 85 – зависимость существует;
0, 6< η < 0, 75 – неявно выраженная зависимость;
η < 0, 6 – зависимости нет;
η =1 – факторы x и y связаны напрямую.
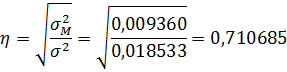
Статистическая значимость эмпирического корреляционного отношения определяется с помощью распределения Фишера.

где N – объем выборки;
k – количество интервалов фактора х. k=8;
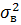 - внутреинтервальная дисперсия.
- внутреинтервальная дисперсия.
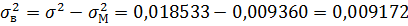
F=7, 57
Распределение Фишера имеет 2 степени свободы.
υ 1=k - 1= 7 υ 2=n – k= 52
Табличное значение распределения Фишера F=2, 2.
Вывод: Расчетное значение Фишера больше табличного, значит, полученному результату можно доверять.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|