
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
6. Лекция: Логические вентили, схемы, структуры
6. Лекция: Логические вентили, схемы, структуры

Рассматриваются основные теоретические (математические, логические) понятия и сведения, касающиеся базовых логических элементов и структур – логических вентилей, логических (переключательных) схем, логической базы аппаратуры ЭВМ и их оптимальной структуры, оптимизации их структур.
Содержание
Любой, самый примитивный компьютер – сложнейшее техническое устройство. Но даже такое сложное устройство, как и все в природе и в технике, состоит их простейших элементов. Любой компьютер, точнее, любой его электронный логический блок состоит из десятков и сотен тысяч так называемых вентилей (логических устройств, базовых логических схем), объединяемых по правилам и законам (аксиомам) алгебры вентилей в схемы, модули.
Логический вентиль (далее – просто вентиль) – это своего рода атом, из которого состоят электронные узлы ЭВМ. Он работает по принципу крана (отсюда и название), открывая или закрывая путь сигналам.
Логические схемы предназначены для реализации различных функций алгебры логики и реализуются с помощью трех базовых логических элементов (вентилей, логических схем или так называемых переключательных схем). Они воспроизводят функции полупроводниковых схем.
Работу вентильных, логических схем мы, как и принято, будем рассматривать в двоичной системе и на математическом, логическом уровне, не затрагивая технические аспекты (аспекты микроэлектроники, системотехники, хотя они и очень важны в технической информатике).
Логические функции отрицания, дизъюнкции и конъюнкции реализуют, соответственно, логические схемы, называемые инвертором, дизъюнктором и конъюнктором.
Логическая функция " инверсия", или отрицание, реализуется логической схемой (вентилем), называемой инвертор.
Принцип его работы можно условно описать следующим образом: если, например, " 0" или " ложь" отождествить с тем, что на вход этого устройства скачкообразно поступило напряжение в 0 вольт, то на выходе получается 1 или " истина", которую можно также отождествить с тем, что на выходе снимается напряжение в 1 вольт.
Аналогично, если предположить, что на входе инвертора будет напряжение в 1 вольт (" истина" ), то на выходе инвертора будет сниматься 0 вольт, то есть " ложь" (схемы на рисунках 6. 1 а, б).

Рис. 6. 1. Принцип работы инвертора
Функцию отрицания можно условно отождествить с электрической схемой соединения в цепи с лампочкой (рис. 6. 2), в которой замкнутая цепь соответствует 1 (" истина" ) или х = 1, а размыкание цепи соответствует 0 (" ложь" ) или х = 0.
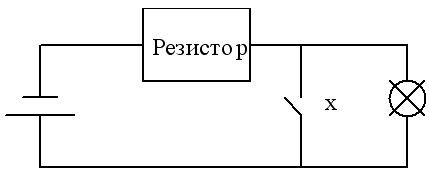
Рис. 6. 2. Электрический аналог схемы инвертора
Дизъюнкцию  реализует логическое устройство (вентиль) называемое дизьюнктор (рис. 6. 3 а, б, в):
реализует логическое устройство (вентиль) называемое дизьюнктор (рис. 6. 3 а, б, в):
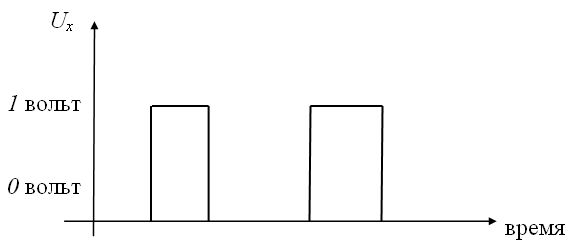
Рис. 6. 3a.
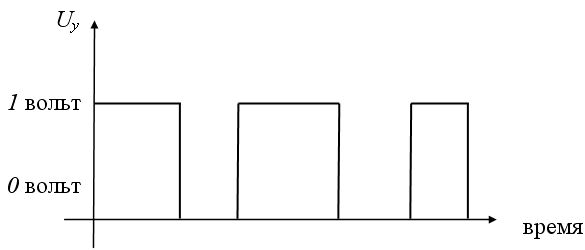
Рис. 6. 3b.
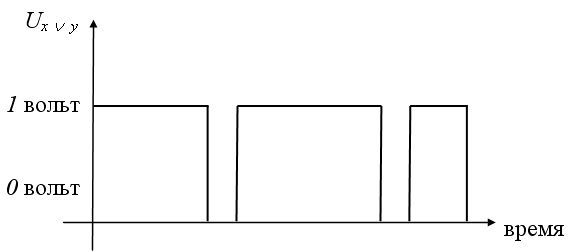
Рис. 6. 3c. Принцип работы дизъюнктора
Дизъюнктор условно изображается схематически электрической цепью вида (рис. 6. 4)
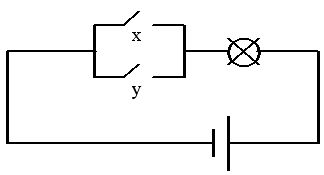
Рис. 6. 4. Электрический аналог схемы дизъюнктора
Конъюнкцию  реализует логическая схема (вентиль), называемая конъюнктором (рис. 6. 5 а, б, в):
реализует логическая схема (вентиль), называемая конъюнктором (рис. 6. 5 а, б, в):
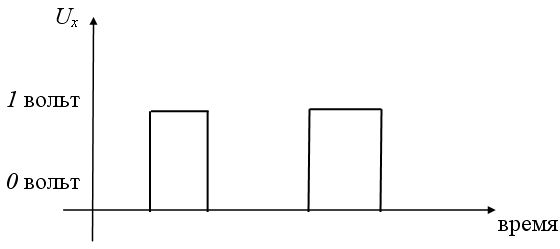
Рис. 6. 5a.
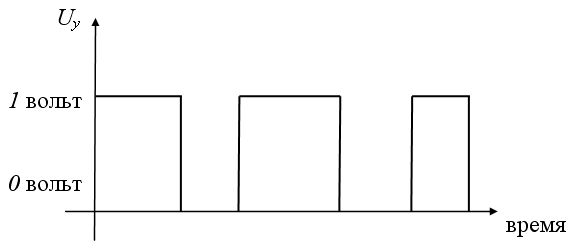
Рис. 6. 5b.
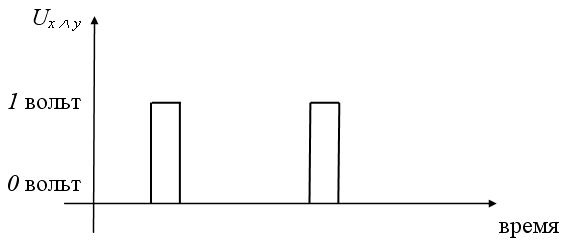
Рис. 6. 5c. Принцип работы конъюнктора
Конъюнктор можно условно изобразить схематически электрической цепью вида (рис. 6. 6)

Рис. 6. 6. Электрический аналог схемы конъюнктора
Схематически инвертор, дизъюнктор и конъюнктор на логических схемах различных устройств можно изображать условно следующим образом (рис. 6. 7 а, б, в). Есть и другие общепринятые формы условных обозначений.
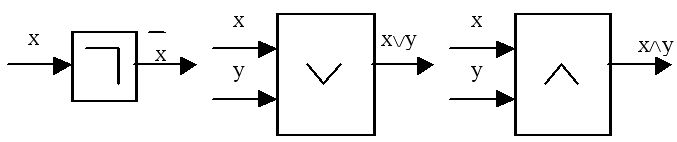
Рис. 6. 7. а, б, в. Условные обозначения вентилей (вариант)
Пример. Транзисторные схемы, соответствующие логическим схемам  (инвертор),
(инвертор), 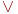 (дизъюнктор),
(дизъюнктор),  (конъюнктор) имеют, например, следующий вид (рис. 6. 8 а, б, в):
(конъюнктор) имеют, например, следующий вид (рис. 6. 8 а, б, в):
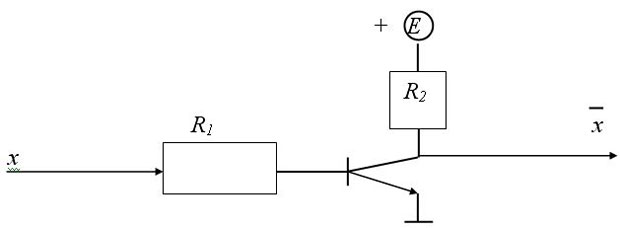
Рис. 6. 8a. Инвертор

Рис. 6. 8b. Дизъюнктор
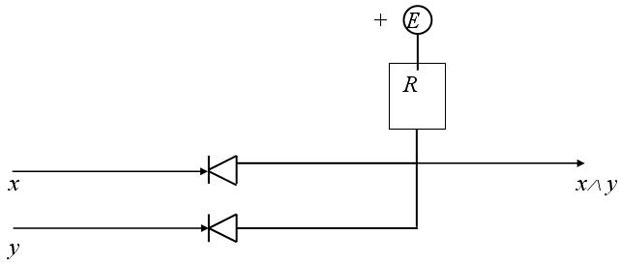
Рис. 6. 8c. Конъюнктор
Из указанных простейших базовых логических элементов собирают, конструируют сложные логические схемы ЭВМ, например, сумматоры, шифраторы, дешифраторы и др. Большие (БИС) и сверхбольшие (СБИС) интегральные схемы содержат в своем составе (на кристалле кремния площадью в несколько квадратных сантиметров) десятки тысяч вентилей. Это возможно еще и потому, что базовый набор логических схем (инвертор, конъюнктор, дизъюнктор) является функционально полным (любую логическую функцию можно представить через эти базовые вентили), представление логических констант в них одинаково (одинаковы электрические сигналы, представляющие 1 и 0) и различные схемы можно " соединять" и " вкладывать" друг в друга (осуществлять композицию и суперпозицию схем).
Таким способом конструируются более сложные узлы ЭВМ – ячейки памяти, регистры, шифраторы, дешифраторы, а также сложнейшие интегральные схемы.
Пример. В двоичной системе таблицу суммирования цифры x и цифры y и получения цифры z с учетом переноса p в некотором разряде чисел x и y можно изобразить таблицей вида
| x | y | z | p |
Эту таблицу можно интерпретировать как совместно изображаемую таблицу логических функций (предикатов) вида
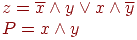
Логический элемент, соответствующий этим функциям, называется одноразрядным сумматором и имеет следующую схему (обозначим ее как  или
или  – если мы хотим акцентировать именно выбранный, текущий i-й разряд) (рис. 6. 9):
– если мы хотим акцентировать именно выбранный, текущий i-й разряд) (рис. 6. 9):
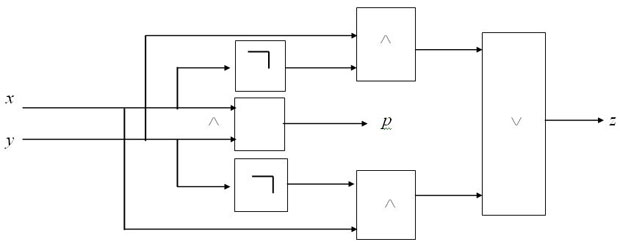
Рис. 6. 9. Схема одноразрядного сумматора
Пример. " Черным ящиком" называется некоторое закрытое устройство (логическая, электрическая или иная схема), содержимое которого неизвестно и может быть определено (идентифицировано) только по отдельным проявлениям входа/выхода ящика (значениям входных и выходных сигналов). В " черном ящике" находится некоторая логическая схема, которая в ответ на некоторую последовательность входных (для ящика) логических констант выдает последовательность логических констант, получаемых после выполнения логической схемы внутри " черного ящика". Определим логическую функцию внутри " черного ящика" (рис. 6. 10), если операции выполняются с логическими константами для входных последовательностей (поразрядно). Например, х = 00011101 соответствует последовательности поступающих значений: " ложь", " ложь", " ложь", " истина", " истина", " истина", " ложь", " истина".

Рис. 6. 10. Схема " черного ящика 1"
Из анализа входных значений (входных сигналов) х, у и поразрядного сравнения логических констант в этих сообщениях с константами в значении z – результате выполнения функции в " черном ящике", видно, что подходит, например, функция вида
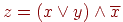
Действительно, в результате " поразрядного" сравнения сигналов (последовательностей значений " истина", " ложь" ) получаем следующие выражения (последовательности логических констант):
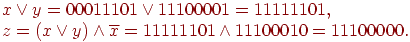
Пример. Попробуйте самостоятельно выписать функцию для " черного ящика"? указанного на рис. 6. 11:

Рис. 6. 11. Схема " черного ящика 2"
Важной задачей (технической информатики) является минимизация числа вентилей для реализации той или иной схемы (устройства), что необходимо для более рационального, эффективного воплощения этих схем, для большей производительности и меньшей стоимости ЭВМ.
Эту задачу решают с помощью методов теоретической информатики (методов булевой алгебры).
Пример. Построим схему для логической функции
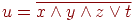
Схема, построенная для этой логической функции, приведена на рис. 6. 12.

Рис. 6. 12. Схема для функции 1
Пример. Определим логическую функцию 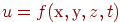 , реализуемую логической схемой вида (рис. 6. 13)
, реализуемую логической схемой вида (рис. 6. 13)

Рис. 6. 13. Схема для функции 2
Искомая логическая функция, если выписать ее последовательно, заполняя " верх" каждой стрелки, будет иметь следующий вид:
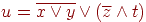

|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|