
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задача 1. Задача 2. Задача 3. Задача 4. Задача 5. Задача 6. Теорема: Если вероятность p наступления события Α в каждом испытании постоянна, то вероятность того, что событие A наступит k раз в n независимых испытаниях, равна: , где .(Формула Бернулли)
РАСЧЕТНО-ГРАФИЧЕСКОЕ ЗАДАНИЕ
ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ
Мартиросовой Юлии Александровны
Зачетная книжка №ХХХХХХХХ
ФТТС
 курс
курс
Группа №5
2014 г.
Задача 1
Необходимо 3 контейнера разместить в 2 складах. Сколькими способами это можно сделать?
Решение
В данной задаче я использовала комбинацию - сочетание без повторений.
Сочетаниями из 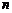 элементов по
элементов по 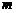
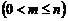 элементов называются соединения, каждое из которых состоит из
элементов называются соединения, каждое из которых состоит из 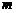 элементов, взятых из данных
элементов, взятых из данных 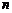 элементов. Эти соединения отличаются друг от друга хотя бы одним элементом. В отличие от размещений, порядок следования элементов здесь не учитывается.
элементов. Эти соединения отличаются друг от друга хотя бы одним элементом. В отличие от размещений, порядок следования элементов здесь не учитывается.
Число сочетаний из 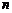 элементов по
элементов по 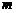 элементов обозначается символом
элементов обозначается символом  и вычисляется по формуле:
и вычисляется по формуле:
 .
.
Я использую сочетание без повторений т. к. :
1- Контейнера в комбинациях участвуют по одному разу и не повторяются
2- В каждой новой комбинации состав контейнеров в складах меняется
3- Порядок размещения контейнеров в складах не важен(т. е., например, комбинации 123 и 321 считаются одинаковыми)
Таким образом, количество способов размещения 3 контейнеров в 2 складах:
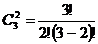 =
= 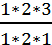 = 3.
= 3.
Задача 2
В ящике находится 9 деталей. Из них 3 бракованных. Наугад из ящика взяли 4 детали. Какова вероятность того, что:
А) все взятые детали окажутся качественными?
Б) ровно 3 детали окажутся качественными?
В) менее 2 деталей окажутся качественными?
Решение
Вероятность (Р) - это отношение числа благоприятных исходов(m) ко всем возможным исходам(n).
Р= 
А) Поскольку для нас благоприятный исход - все 4 взятые детали качественные (всего в ящике 6 качественных деталей), а все возможные исходы – 4 любые детали взятые из 9, то вычислим вероятность, используя сочетания (т. к. нам не важен порядок в комбинациях из деталей):
Р(А)=  =
= 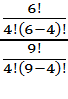 =
= 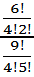 =
= 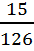 = 0. 1190476
= 0. 1190476
Б) Благоприятный исход – ровно 3 из взятых 4 деталей качественные (всего качественных 6), соответственно 1 деталь бракованная (всего бракованных 3). Все возможные исходы - 4 любые детали взятые из 9. Вероятность вычислим используя сочетания и правило умножения(т. к. из 4 выбранных деталей 3 качественные И (! ) 1 бракованная).
Правило умножения (основной принцип): если из некоторого конечного множества первый объект (элемент 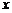 ) можно выбрать
) можно выбрать 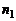 способами и после каждого такого выбора второй объект (элемент
способами и после каждого такого выбора второй объект (элемент 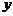 ) можно выбрать
) можно выбрать 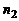 способами, то оба объекта (
способами, то оба объекта ( 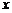 и
и 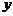 ) в указанном порядке можно выбрать
) в указанном порядке можно выбрать 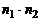 способами.
способами.
Р(Б)= 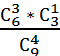 =
= 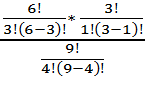 =
=  =
= 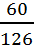 = 0. 4761904
= 0. 4761904
В) Благоприятный исход – 1 деталь будет качественной и 3 бракованные. Все возможные исходы - 4 любые детали взятые из 9. Вероятность вычислим используя сочетания и правило умножения(т. к. из 4 выбранных деталей 1 качественная И (! ) 3 бракованные):
Р(В)= 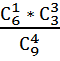 =
=  =
= 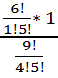 =
=  = 0. 047619
= 0. 047619
Задача 3
Набирая номер телефона, абонент забыл последние 2 цифры и набрал их наугад. Найти вероятность того, что он дозвонился, если:
А) он знает, что все цифры не повторяются.
Б) он знает, что все цифры совпадают.
В) он не имел никакой дополнительной информации.
Решение
Всего есть 10 цифр(0, 1, 2, 3, 4, 5, 6, 7, 8, 9).
А) Благоприятный исход здесь один – правильный набор последних цифр (m=1). Всех возможных исходов здесь будет столько, сколько можно составить комбинаций из 2 цифр, порядок которых имеет значение, значитвычисляем вероятность с помощью размещений.
Размещениями из 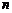 элементов по
элементов по 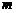
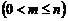 элементов называются соединения, каждое из которых состоит из
элементов называются соединения, каждое из которых состоит из 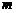 элементов, взятых из данных
элементов, взятых из данных 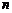 элементов. При этом размещения отличаются друг от друга как самими элементами, так и их порядком.
элементов. При этом размещения отличаются друг от друга как самими элементами, так и их порядком.
Число размещений из 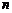 элементов по
элементов по 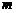 элементов обозначается символом
элементов обозначается символом 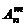 и вычисляется по формуле:
и вычисляется по формуле:
 , где
, где 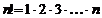 ,
, 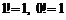 .
.
Вероятность того, что абонент дозвонился, если он знает, что все цифры не повторяются:
P(A)= 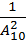 =
= 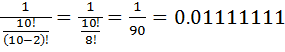
Б) Аналогично условию А), благоприятный исход здесь один – правильный набор последних цифр (m=1). Всех возможных исходов здесь будет столько, сколько можно составить комбинаций из 2 цифр, порядок которых имеет значение, НО которые при этом совпадают, значитвычисляем вероятность с помощью размещений с повторениями:
P(Б)= 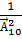 =
= 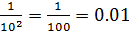
В) Если абонент не имел никакой дополнительной информации, то набранные 2 цифры могут быть ИЛИ разные, ИЛИ одинаковые (события несовместны). Тогда вероятность суммы двух событий равняется сумме двух вероятностей(согласно теореме сложения вероятностей ).
Получаем:
P(A+Б)=Р(А)+Р(Б)= 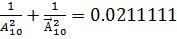
Задача 4
Курс лекций состоит из 3 тем. Вероятность того, что студент успешно сдаст первую тему равна 0. 12. Вероятность того, что он успешно сдаст каждую последующую тему больше предыдущей на 0. 1. Найти вероятность того, что:
А) студент успешно сдаст все темы;
Б) студент не сдаст ни одной темы;
В) студент успешно сдаст ровно 1 тему;
Г) студент успешно сдаст по крайней мере одну тему;
Д) студент не сдаст по крайней мере одну тему.
Решение
Вероятность того, что студент успешно сдаст 1 тему равна 0. 12; вторую тему – 0. 22; третью тему – 0. 32.
Вероятность того, что студент не сдаст 1 тему равна 0. 88; вторую – 0. 78; третью – 0. 68 (Так как Сумма вероятностей противоположных событий равна единице)
А) Так как наши события независимы (появления каждого из них не зависит от того, появилось другое событие или нет, и появление одного события не изменяет вероятности другого события). Воспользуемся Теоремой умножения для независимых событий
Теорема. Вероятность произведения независимых событий равна произведению их вероятностей:
| P(AB) = P(A)*P(B). |
Р( 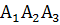 )= Р(
)= Р( 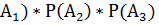 = 0, 12*0, 22*0, 32=0. 008448
= 0, 12*0, 22*0, 32=0. 008448
Б) Аналогично:
Р( 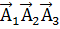 )= Р(
)= Р( 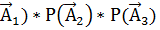 = 0, 88*0, 78*0, 68=0. 466752
= 0, 88*0, 78*0, 68=0. 466752
В) Вероятность что студент успешно сдаст ровно одну тему, означает что он сдаст одну и не сдаст две темы. Тогда вероятность будет равна сумме вероятностей успешной сдачи каждой из трех тем и не сдачи двух других:
Р( 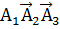 )= Р(
)= Р( 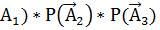 = 0, 12*0, 78*0, 68=0. 063648
= 0, 12*0, 78*0, 68=0. 063648
Р( 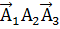 )= Р(
)= Р( 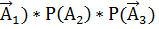 = 0, 88*0, 22*0, 68=0. 131648
= 0, 88*0, 22*0, 68=0. 131648
Р( 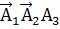 )= Р(
)= Р( 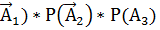 = 0, 88*0, 78*0, 32=0. 219648
= 0, 88*0, 78*0, 32=0. 219648
Р( 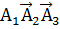 )+Р(
)+Р( 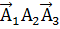 )+Р(
)+Р( 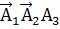 )= 0. 063648+0. 131648+0. 219648=0, 414944
)= 0. 063648+0. 131648+0. 219648=0, 414944
Г) Так как вероятность, что студент успешно сдаст по крайней мере одну тему - событие противоположное тому, что студент не сдаст ни одной темы, то эту вероятность вычислим:
Р( 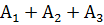 )=1-Р(
)=1-Р( 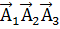 )=1-0. 466752=0, 533248
)=1-0. 466752=0, 533248
Д) Так как вероятность, что студент не сдаст по крайней мере одну тему-событие противоположное тому, что студент успешно сдаст все темы, то эту вероятность вычислим:
Р( 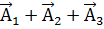 )= 1- Р(
)= 1- Р( 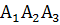 )= 1-0. 008448=0. 991552
)= 1-0. 008448=0. 991552
Задача 5
Продукция завода производится в 4 цехах. 1й цех производит 5%; 2й – 15%; 3й – 25%; 4й – 55% от всей продукции завода. 1й цех выпускает бракованное изделие с вероятностью 0. 083, 2й цех – с вероятностью 0. 11, 3й цех – с вероятностью 0. 11, 4й цех – с вероятностью 0. 2.
А) Какова вероятность того, что выбранное наугад из всего объема выпущенной заводом продукции изделие окажется бракованным?
Б) Извлеченное наугад изделие оказалось бракованным. Какова вероятность того, что это изделие было произведено во 2м цеху?
Решение
При решении данной задачи следует применить формулу полной вероятности и формулу Байеса.
Формула полной вероятности:
Пусть событие A может наступить только с одним из nпопарно несовместных событий 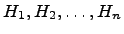 , которые по отношению кА называются гипотезами. Тогда вероятность событияА можно вычислить по формуле полной вероятности:
, которые по отношению кА называются гипотезами. Тогда вероятность событияА можно вычислить по формуле полной вероятности:
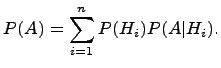
Если стало известно, что событиеА произошло, то вероятность 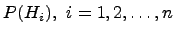 можно переоценить, т. е. найти условные вероятности
можно переоценить, т. е. найти условные вероятности 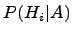 . Эта задача решается по формуле Байеса:
. Эта задача решается по формуле Байеса:
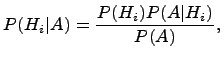
где 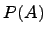 вычисляется по формуле полной вероятности.
вычисляется по формуле полной вероятности.
Пусть событие А= 
Выдвигаем 4 гипотезы:
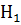 =
=  ; Р(
; Р( 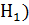 =0. 05; Р(
=0. 05; Р( 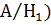 =0. 083
=0. 083
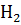 =
= 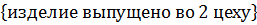 ; Р(
; Р( 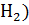 =0. 15; Р(
=0. 15; Р( 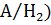 =0. 11
=0. 11
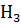 =
= 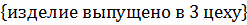 ; Р(
; Р( 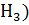 =0. 25; Р(
=0. 25; Р(  =0. 11
=0. 11
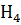 =
= 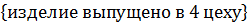 ; Р(
; Р( 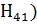 =0. 55; Р(
=0. 55; Р( 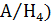 =0. 2
=0. 2
А)Вероятность того, что выбранное наугад из всего объема выпущенной заводом продукции изделие окажется бракованным:
Р(А) = 0. 05*0. 082+0. 15*0. 11+0. 25*0. 11+0. 55*0. 2=0. 1581
Б) Вероятность того, что извлеченное наугад бракованное изделие было произведено во 2м цеху:
Р( 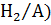 =
= 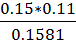 =0. 1043643
=0. 1043643
Задача 6
По цели производится 15 выстрелов. Вероятность попадания в каждом выстреле равна 0, 66. Какова вероятность того, что цель будет поражена ровно 2 раза?
Решение
Теорема: Если вероятность p наступления события Α в каждом испытании постоянна, то вероятность того, что событие A наступит k раз в n независимых испытаниях, равна: , где. (Формула Бернулли)
Если цель поражена ровно 2 раза из 15, то:
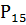 (2) =
(2) = 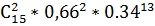 =
= 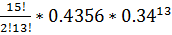 =0. 000037
=0. 000037
Задача 7
Вероятность выпуска бракованного изделия составляет 0. 01. Какова вероятность того, что среди 1000 отобранных изделий:
А) не более 12 изделий окажется бракованных?
Б) количество бракованных изделий будет от 12 до 52?
Решение
A) Т. к. в событии, состоящем в том, что отобранные изделия окажутся бракованными: число испытаний (отбор 1000 изделий)-n велико, вероятностьвыпуска бракованного изделия-р мала, а посчитать требуется вероятность, что не более 12 изделий будут бракованные (не менее, чем 0 изделий и не более, чем 12 изделий), то уместно будет использовать Интегральную теорему Лапласа.
Интегральная теорема Лапласа.
Если вероятность события А равна (0 < р < 1), то вероятность, что событие А произойдет в серии из n-испытаний не менее, чем k1 раз и не более k2 разприближенно равна:
P(k1; k2)=Φ (x'') - Φ (x'), где
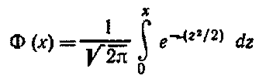 - функция Лапласа (функция табулирована);
- функция Лапласа (функция табулирована);
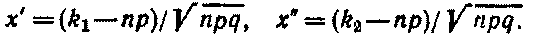
По условию нашей задачи:
n=1000; p=0. 01;
Тогда: q=1-p=1-0. 01=0. 99;
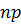 =1000*0. 01=10;
=1000*0. 01=10;
npq=1000*0. 01*0. 99=9, 9.
Таким образом, вероятность того, что не более 12 изделий окажется бракованных равна:
P(A)= 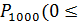 k
k 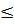 12)
12) 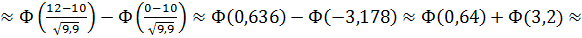 0, 2389+0, 49931
0, 2389+0, 49931 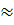 0, 73821
0, 73821
Б) Т. к. в событии, состоящем в том, что отобранные изделия окажутся бракованными: число испытаний (отбор 1000 изделий)-n велико, вероятность выпуска бракованного изделия-р мала, а посчитать требуется вероятность, что количество бракованных изделий будет от 12 до 52 (не менее, чем 12 изделий и не более, чем 52 изделия), то следует снова использовать Интегральную теорему Лапласа.
По условию нашей задачи:
n=1000; p=0. 01;
Тогда: q=1-p=1-0. 01=0. 99;
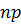 =1000*0. 01=10;
=1000*0. 01=10;
npq=1000*0. 01*0. 99=9, 9.
Таким образом, вероятность того, что количество бракованных изделий будет от 12 до 52:
P(Б)= 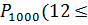 k
k 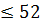 )
) 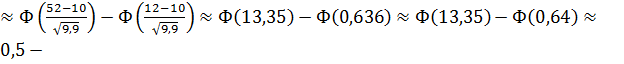 0, 2389
0, 2389 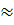 0, 2611
0, 2611
Задача 8
Случайная величина Х задана законом распределения:
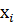
| -2 | |||||
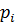
| 2/100 | 1/10 | 20/100 | 4/10 | 2/10 | 8/100 |
Вычислить математическое ожидание М(Х), дисперсию D(X) и среднеквадратическое отклонение 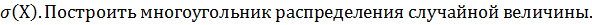
Решение:
Сначала проверим, равна ли сумма вероятностей всех значений 1:
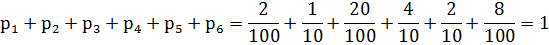
Математическое ожидание находим по формуле m = ∑ xipi.
M(Х) = (2/100) × (-2) + (1/10) × (0) + (2/10) × (1) + (4/10) × (2) + (2/10) × (3) + (8/100) × (6) = 2. 04
Дисперсию находим по формуле d = ∑ x2ipi - M[x]2.
D(X)=(2/100) × (-2)2 + (1/10) × (0)2 + (2/10) × (1)2 + (4/10) × (2)2 + (2/10) × (3)2 + (8/100) × (6)2- 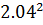 =6. 56-4. 1616=2. 3984
=6. 56-4. 1616=2. 3984
Среднее квадратическое отклонение σ (x).
σ = 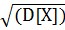 =
=  = 1. 549
= 1. 549
Введем прямоугольную систему координат ХОР и отметим в ней точки:
(-2; 0, 02), (0; 0, 1), (1; 0, 2), (2; 0, 4), (3; 0. 2) и (6; 0, 08). Последовательно соединив их, построим многоугольник распределения.
Задача 9
Монета бросается 3 раза. Записать закон распределения случайной величины Х, равной количеству выпадений решки. 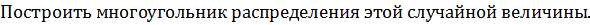
Решение
Возможные значения случайной величины: 0, 1, 2, 3, которые соответствуют количеству возможных выпадений решки (0 из 3 раз, 1 из 3, 2 из 3, 3 из 3). Соответствующие им вероятности:
P(0)=1/8; Р(1)=3/8; Р(2)=3/8; Р(3)=1/8
Закон распрделенияСВ будет иметь вид:
| xi | ||||
| pi | 1/8 | 3/8 | 3/8 | 1/8 |
∑ pi = 1/8+3/8+3/8+1/8=1
Введем прямоугольную систему координат ХОР и отметим в ней точки:
(0; 1/8), (1; 3/8), (2; 3/8), (3; 1/8). Последовательно соединив их, построим многоугольник распределения.
Задача 10
В среднем за сутки на элеватор прибывает 10 грузовиков. Предполагается, что последовательность прибывающих грузовиков образует простейший поток событий. Найти вероятность того, что
А) в течение заданного 1 часа на элеватор прибудет ровно 2 грузовика;
Б) в течение заданных 3 часов на элеватор не прибудет ни одного грузовика;
В) в течение заданного 1 часа на элеватор прибудет не более 2 грузовиков;
Г) в течение заданного 1 часа на элеватор прибудет больше 2 грузовиков.
Решение
Под потоком событий в теории вероятностей понимается последовательность событий, происходящих одно за другим в какие-то моменты времени. Простейшим потоком однородных событий называем всякий стационарный ординарный поток без последействия. Одной из характеристик потока случайных событий является его интенсивность – среднее число событий, происходящих в единицу времени.
Пусть простейший поток событий имеет интенсивность λ, тогда вероятность появления k-событий за интервал времени tравен:
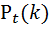 =
= 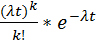
Исходя из этой формулы, находим:
А) λ =10/24=0. 417(среднее количество прибывающих грузовиков за час);
t=1 (ч); k=2 (грузовиков)
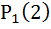 =
= 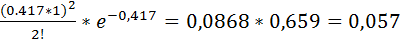 -вероятность того, что в течение заданного 1 часа на элеватор прибудет ровно 2 грузовика.
-вероятность того, что в течение заданного 1 часа на элеватор прибудет ровно 2 грузовика.
Б)λ =10/24=0. 417(среднее количество прибывающих грузовиков за час);
t=3 (ч); k=0 (грузовиков)
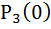 =
= 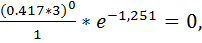 286 – вероятность, что в течение заданных 3 часов на элеватор не прибудет ни одного грузовика
286 – вероятность, что в течение заданных 3 часов на элеватор не прибудет ни одного грузовика
В) λ =10/24=0. 417(среднее количество прибывающих грузовиков за час);
t=1 (ч); k≤ 2 (грузовиков)
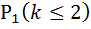 =
= 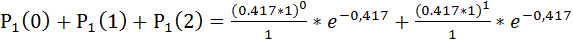 +
+ 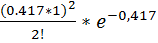 =0, 659+0, 275+0, 057=0, 991 –вероятность, что в течение заданного 1 часа на элеватор прибудет не более 2 грузовиков
=0, 659+0, 275+0, 057=0, 991 –вероятность, что в течение заданного 1 часа на элеватор прибудет не более 2 грузовиков
Г) λ =10/24=0. 417(среднее количество прибывающих грузовиков за час);
t=1 (ч); k 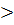 2 (грузовиков)
2 (грузовиков)
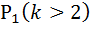 =1-
=1- 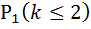 =1-0. 991=0, 009 – вероятность, что в течение заданного 1 часа на элеватор прибудет больше 2 грузовиков.
=1-0. 991=0, 009 – вероятность, что в течение заданного 1 часа на элеватор прибудет больше 2 грузовиков.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|