
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА № 1.
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА № 1.
По разделу «Элементы теории вероятностей»
Варианты заданий для расчетной работы определяются по порядковому номеру студента в списке группы.
Замечание: буквой V обозначен номер варианта.
Задание к задачам № 1. 1 -1. 4
1. Переписать текст задачи, заменяя все параметры их значениями для решаемого варианта.
2. Определить испытания и элементарные события.
3. Определить исследуемое событие А и другие события.
4. Установить, какие формулы следует использовать для вычислений и выполнить последние. Вычисления произвести, по возможности, точно.
Задача 1. 1. В урне содержится К черных и Н белых шаров. Случайным образом вынимают М шаров. Найти вероятность того, что среди них имеется:
а) Р белых шаров; б) меньше, чем Р, белых шаров; в) хотя бы один белый шар.
Значения параметров К, Н, М и Р по вариантам приведены в табл. 1.
Таблица 1.
| Вариант | ||||||||||||||||
| К | ||||||||||||||||
| Н | ||||||||||||||||
| М | ||||||||||||||||
| Р | ||||||||||||||||
|
| ||||||||||||||||
| Вариант | ||||||||||||||||
| К | ||||||||||||||||
| Н | ||||||||||||||||
| М | ||||||||||||||||
| Р | ||||||||||||||||
Задача 1. 2. Устройство состоит из трех независимых элементов, работающих в течение времени Т безотказно соответственно с вероятностями 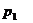 ,
, 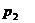 и
и 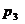 . Найти вероятность того, что за время Т выйдет из строя: а) только один элемент; б) хотя бы один элемент.
. Найти вероятность того, что за время Т выйдет из строя: а) только один элемент; б) хотя бы один элемент.
Значения параметров вычислить по следующим формулам:
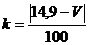 ;
;
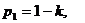
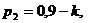
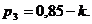
Задача 1. 3. В пирамиде стоят R винтовок, из них L, с оптическим прицелом. Стрелок, стреляя из винтовки с оптическим прицелом, может поразить мишень с вероятностью 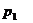 , а, стреляя из винтовки без оптического прицела, — с вероятностью
, а, стреляя из винтовки без оптического прицела, — с вероятностью 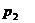 . Найти вероятность того, что стрелок поразит мишень, стреляя из случайно взятой винтовки.
. Найти вероятность того, что стрелок поразит мишень, стреляя из случайно взятой винтовки.
Значения параметров вычислить по следующим формулам:
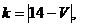
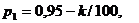
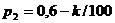
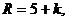
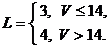
Задача 1. 4. В монтажном цехе к устройству присоединяется электродвигатель. Электродвигатели поставляются тремя заводами-изготовителями. На складе имеются электродвигатели этих заводов соответственно в количестве 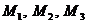 штук, которые могут безотказно работать до конца гарантийного срока с вероятностями соответственно
штук, которые могут безотказно работать до конца гарантийного срока с вероятностями соответственно 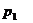 ,
, 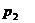 и
и 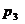 . Рабочий берет случайно один электродвигатель и монтирует его к устройству. Найти вероятности того, что смонтированный и работающий безотказно до конца гарантийного срока электродвигатель поставлен соответственно первым, вторым или третьим заводом-изготовителем.
. Рабочий берет случайно один электродвигатель и монтирует его к устройству. Найти вероятности того, что смонтированный и работающий безотказно до конца гарантийного срока электродвигатель поставлен соответственно первым, вторым или третьим заводом-изготовителем.
Значения параметров вычислить по следующим формулам:
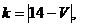
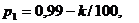
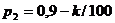
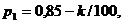
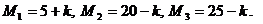
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|