
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
2 Расчеты
2. 1 Сбор нагрузок
2. 1. 1 Постоянная
Постоянные нагрузки от покрытия
Таблица 1
| Состав покрытия | Нормативная нагрузка, кН/м2 | Коэффициент надежности по нагрузке | Расчётная нагрузка, кН/м2 |
| Защитный слой (битумная мастика с втопленным гравием Гидроизоляция (4 слоя рубероида) Утеплитель (минераловатные плиты повышенной жесткости) ρ =200 кг/м2, t=90 мм Пароизоляция (один слой рубероида) Стальная панель с профилированным настилом Собственная масса металлических конструкций шатра (фермы, фонари, связи) | 0. 4 0. 2 0. 18 0. 05 0. 35 0. 3 | 1. 3 1. 3 1. 2 1. 3 1. 05 1. 05 | 0. 52 0. 26 0. 22 0. 07 0. 37 0. 32 |
| Итого | gn=0. 48 | g=1. 76 |
Постоянная равномерно распределённая линейная нагрузка на ригель равна:
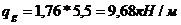
Опорная реакция ригеля: 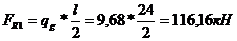
где: 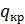 - расчётная распределённая постоянная нагрузка;
- расчётная распределённая постоянная нагрузка;
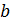 - шаг поперечных рам;
- шаг поперечных рам;
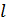 – пролёт поперечной рамы.
– пролёт поперечной рамы.
2. 1. 2 Снеговая
Расчётное значение веса снегового покрова принято 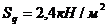 [2].
[2].
Линейная распределённая нагрузка от снега на ригель рамы:
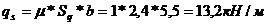
Опорная реакция ригеля:
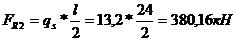
2. 1. 3 Ветровая
Принимаем: w0=0. 23
Ветровой район I
Тип местности B (см. прил. 3 [1])
Коэфициент k при высоте до 10 м – 0. 65; для 20 м – 0. 85; для 30 м – 0. 98
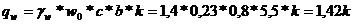
Линейная распределённая нагрузка при высоте до
10 м равна 1, 42 ∙ 0. 65 = 0, 923 кН/м;
20 м – 1, 42 ∙ 0. 85 =1, 207 кН/м;
30м - 1, 42 ∙ 0. 98 = 1, 3916 кН/м;
18м – 0, 923+ (1, 207-0, 923)∙ 8/10 = 1, 15 кН/м – q1
20. 40м – 1, 207+ (1, 3916-1, 207)∙ 0. 95/10 = 1, 225кН/м – q2
Вычисляем сосредоточенные силы от ветровой нагрузки
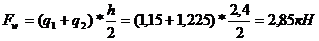
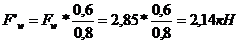 .
.
Эквивалентные линейные нагрузки находим по формуле 12. 10 [1]
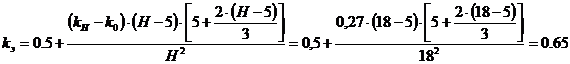
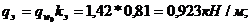
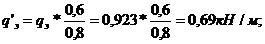
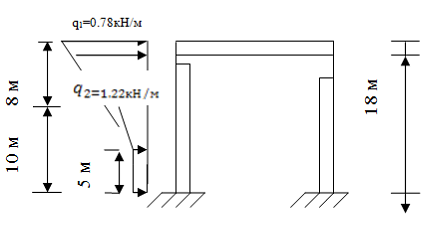
Рисунок 5 - Схема ветровых нагрузок
Пространственная жёсткость здания создаётся системой плоских ограждающих элементов, продольных и поперечных стен с жёстким диском покрытия, в пространственный блок. В этом блоке продольные стены обеспечивают горизонтальную продольную жёсткость, а торцевые стены – поперечную жёсткость. Основные колонны, вертикальные связи между ними и обшивка профнастилом создают жёсткость продольных стен. Стойки торцевого фахверка, вертикальные связи по ним и обшивка профнастилом определяют жёсткость поперечных стен. Продольные и поперечные стены здания связывает в единую пространственную систему жёсткий диск покрытия. Жёсткость диска покрытия создают стропильные фермы, связи, прогоны и обшивка из стального профилированного настила.
2. 2 Статический расчет
2. 2. 1 Расчет конструкции
Расчёт на постоянные нагрузки:
Продольное усилие в стойках равно:
. N=(13, 2+9, 68)*24/2=274, 56кН
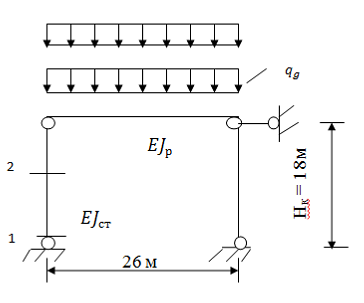
Рисунок 6 – Расчетная схема и нагрузки
Расчёт на снеговые нагрузки:
Расчёт выполняется аналогично предыдущему. Изгибающие моменты и поперечные силы в стойках равны нулю. Продольная сила в стойках равна величине опорной реакции ригеля от снега.
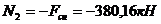 .
.
Наибольший изгибающий момент от ветра в средней части левой стойки (сечение 2).
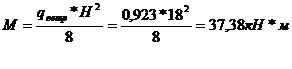
2. 2. 2 Расчет фермы
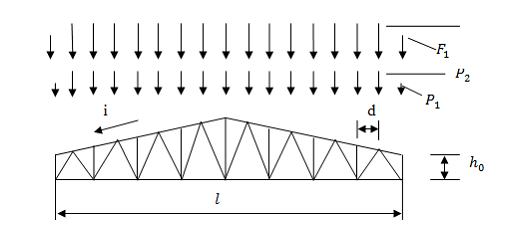
Рисунок 8 – Компоновочные размеры фермы
Узловые нагрузки:
Р1= qкр· b · 0, 5 · d = 1. 76 · 5. 5 · 0. 5 ∙ 3. 25 = 15, 7кН.
Р2= qкр· b · d = 1. 76 · 5. 5 · 3. 25 = 31, 4кН.
F1 = pсн · b ·0. 5 · d = 2. 4 · 5. 5 · 0. 5 · 3. 25 = 21, 6кН.
F2 = pсн · b · d = 2. 4 · 5. 5 · 3. 25 = 44кН.
При шарнирном сопряжении ригеля с колонной можно определять усилия в стержнях фермы от одного нагружения –( постоянная + снег).
При этом, расчётная узловая нагрузка равна:
S=P2+F2=31, 4+44=75, 4кН.
В данной работе определяем расчётные усилия в стержнях фермы и прогибы узлов с помощью компьютерной программы «Лира 9. 2».
Таблица 2
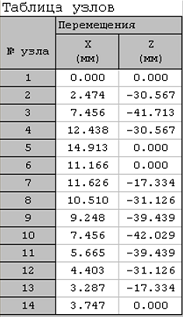
2. 3 Расчет сечений стержней фермы
Определяются требуемые характеристики сечений стержней фермы:
Для сжатых стержней - 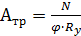 ;
; 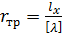 .
.
Для растянутых стержней - 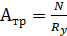 ;
; 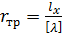 .
.
Таблица 3 Проверка стержней " в плоскости фермы" (тавры и уголки)
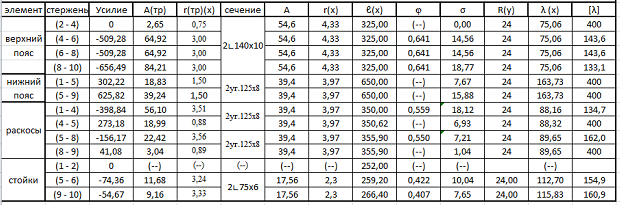
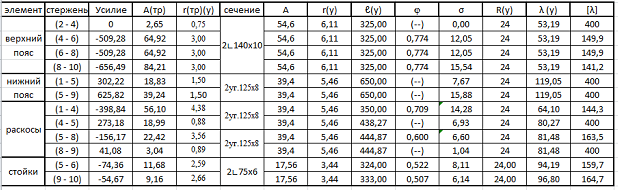
Таблица 4 – Проверка стержней " из плоскости фермы" (тавры и уголки)
2. 4 Расчет колонны
2. 4. 1 Подбор сечения стержня колонны
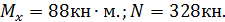
Принимаем сечение стержня: Ι 35Б2(сквозной двутавр).
А=45. 6 см2;
Wx=819. 8 см3;
ix =24. 5 см;
iy = 3. 36 см;
m = 59. 8 кг/м.
Расчётные длины:
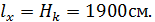
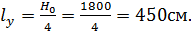
Относительный эксцентриситет усилия сжатия:
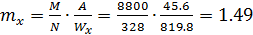 ;
;
Условная гибкость «в плоскости рамы»:
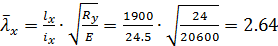 ;
;
Гибкость стержня « плоскости изгибающего момента - 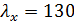 . Предельно допускаемая гибкость ([2], стр. 24, таб. 19; 20) - [
. Предельно допускаемая гибкость ([2], стр. 24, таб. 19; 20) - [ 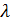 ]=141.
]=141.
Условная гибкость «из плоскости рамы»:
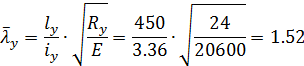
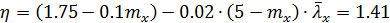
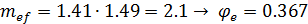
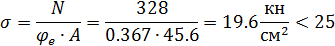
Проверка устойчивости из плоскости рамы ([2] п. 5. 3, стр. 9):
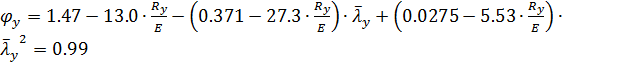
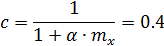
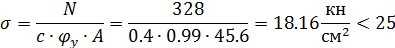
2. 4. 2 Расчет базы колонны
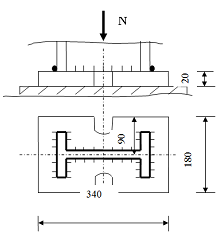
Принимаем бетон фундамента класса В10 ([1], стр. 250. таб. 8. 4) Из условия прочности бетона фундамента на смятие, определим требуемую площадь опорной плиты базы:
| где: Ширину опорной плиты принимаем конструктивно, по ширине полки стержня колонны:
|
|
Рисунок 9 – Схема базы колонны
Расчётная длина плиты:
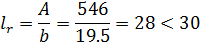
| |
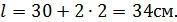
Для определения толщины плиты рассмотрим участок между полками стержня колонны. Напряжение в бетоне под опорной плитой:
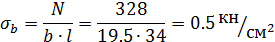
Изгибающий момент определяется для плиты, опёртой на три стороны, с отношением сторон более двух ([1], стр. 251, таб. 8. 5):
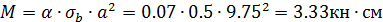
Толщина опорной плиты базы определяется из условия прочности на изгиб:
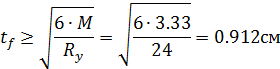
Принимаем толщину плиты опорной плиты базы колонны – 20мм.
Два анкерных болта принимаем диаметром 20мм.
2. 4. 3 Расчет оголовка колонны
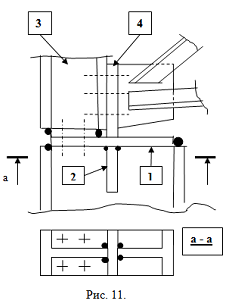
|
Конструкция оголовка состоит из: опорной плиты – 1;
опорного ребра – 2;
надколонника – 3.
Давление фермы на колонну передаёт фланец опорного узла фермы – 4, через опорное ребро оголовка – 2. Толщина плиты оголовка принимается конструктивно 14мм. Длина вертикальных сварных швов, соединяющих опорное ребро со стенкой колонны, рассчитывается на действие этого давления – величину опорной реакции фермы.
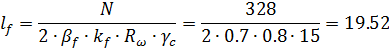
Высота опорного ребра:
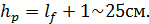
Рисунок 10 – Схема оголовка колонны
Толщину ребра оголовка определяем из условия прочности на смятие:
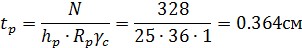
Толщину опорного ребра оголовка назначаем конструктивно – 10мм.
Назначив толщину ребра, следует проверить его на срез:
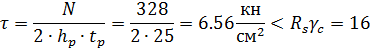
Условие прочности ребра на срез выполняется.
Также необходима проверка на срез стенки колонны:
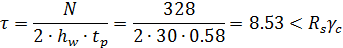
Болты, соединяющие опорный фланец фермы с надколонником и опорную плиту оголовка с надколонником, принимаются конструктивно, диаметром 18 – 20мм.
2. 4. 4 Расчет массы колонны
Стержень - 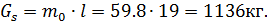
Плита базы - 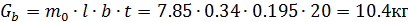
Плита оголовка - 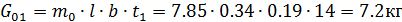
Ребро оголовка - 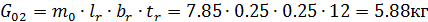 .
.
Общая масса колонны – 1159. 6 кг.
Список литературы
1. Кудишин Ю. И. «Металлические конструкции». М. 2006.
2. СНиП 2-23-81*. Москва 2003.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|

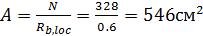 ,
, 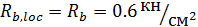 .
. 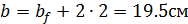 .
.