Контакты

Случайная статья

Метод Франка-Вулфа в задачах многокритериальной оптимизации

Стр 1 из 2Следующая ⇒

Метод Франка-Вулфа в задачах многокритериальной оптимизации

Рассмотрим более подробно метод Франка-Вулфа, как один из эффективныхинструментов, используемых при решении многокритериальных аналитических задачна основе построенияобобщенного скалярного критерия, методом 2идеальной точки» и т. д.

Решается задача

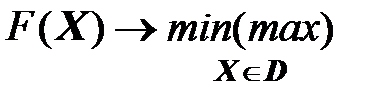(1)

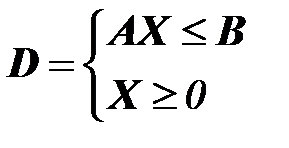(2)

Алгоритм метода Франка-Вулфа.

Начальный этап

Задать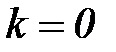

Задать 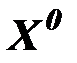– начальное приближение

Вычислить градиент: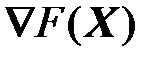

Шаг1. Составить вспомогательную функцию:

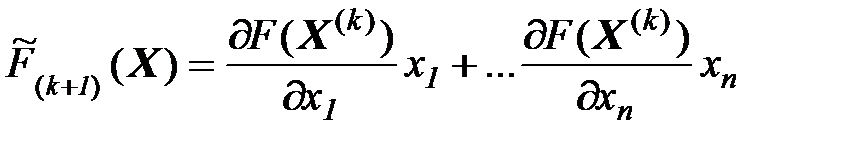
Решить задачу ЛП:

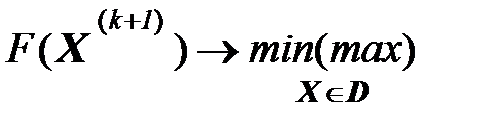(3)

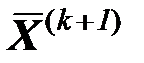-решение задачи (3).

Шаг 2. Искать приближение

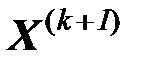к решению задачи (1), (2) в виде:

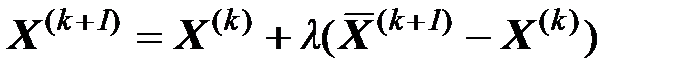(4)

где 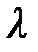есть решение задачи: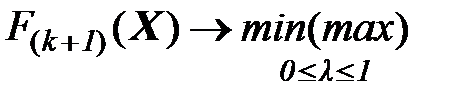

(если получим 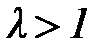, то полагаем )

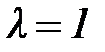вычисляем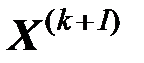

вычисляем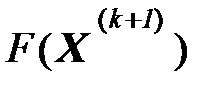

Шаг3.

Проверяем выполнение критерия останова.

Если критерий останова выполняется, то полагаем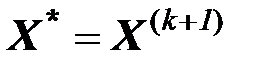

Решение найдено.

Иначе, полагаем , переходим к шагу 1.

Задача.

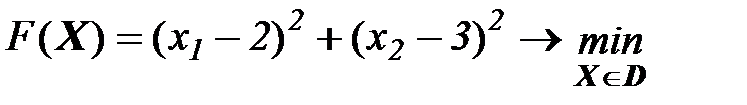(1)

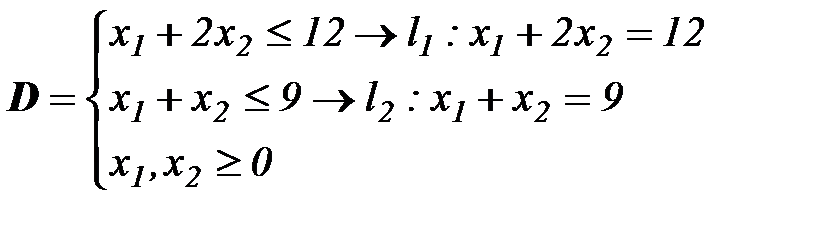(2)

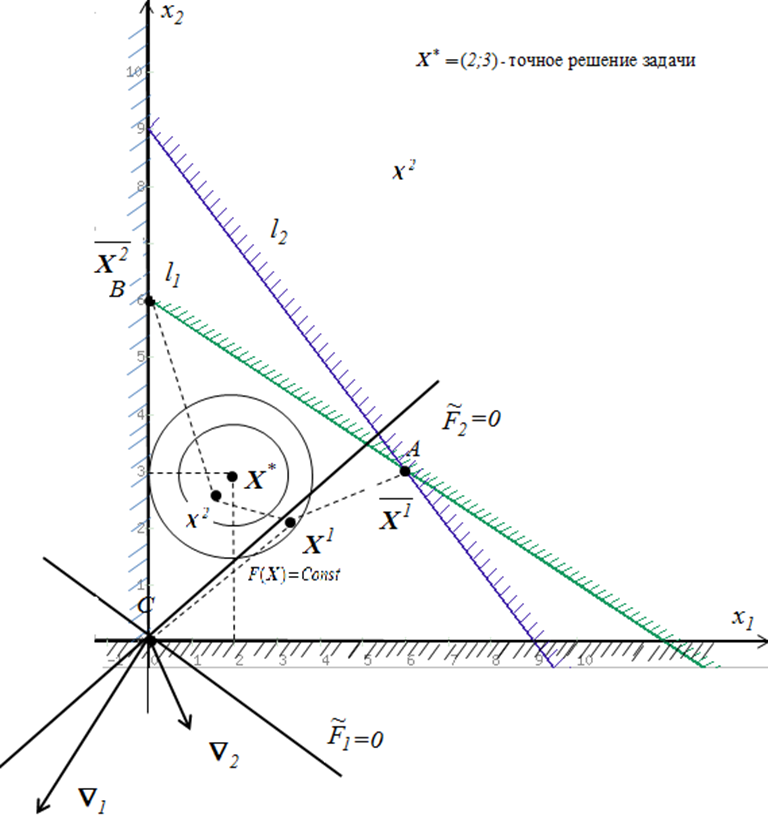
Начальный этап.

Выбираем 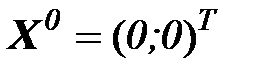- начальное приближение;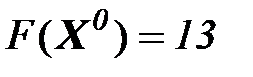

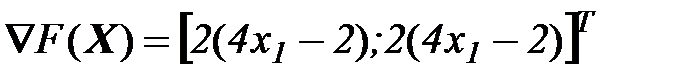
Шаг 1. Решаем задачу:

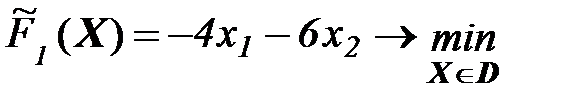(3)

где D задано в виде (2).

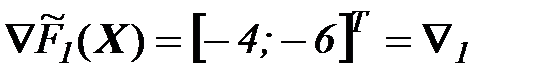
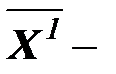точка пересечения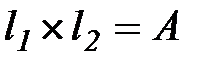

Для этого решаем систему уравнений:

Шаг 2.

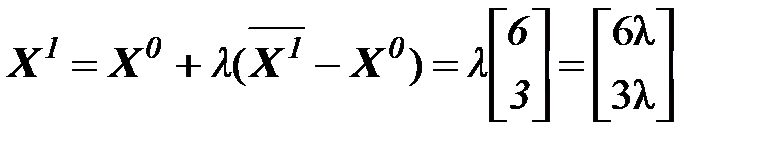
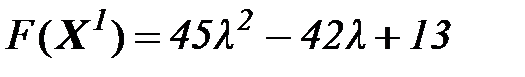
Решаем задачу:

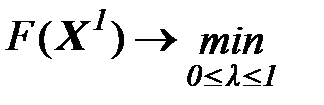(4)

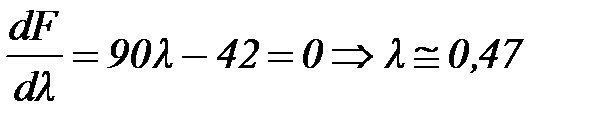
Следовательно:

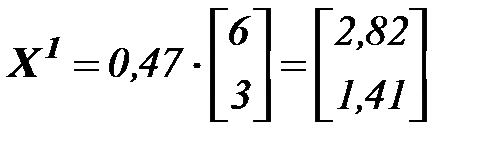
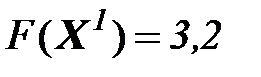
Шаг 3. Сформируем вспомогательную функцию:

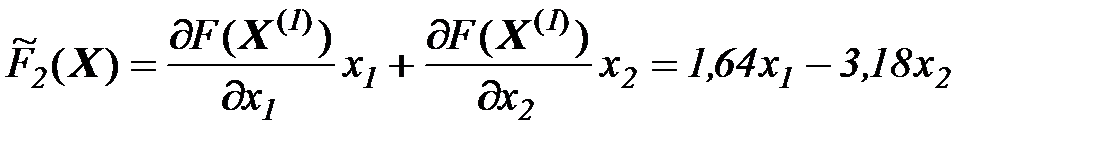
Решаем задачу:

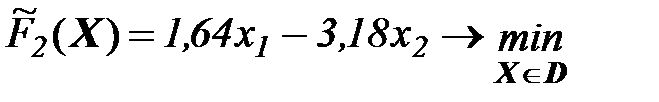(5)

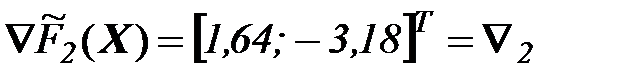
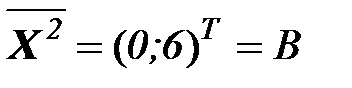
Шаг 4. Вычисляем:

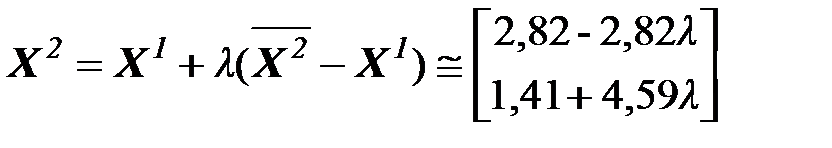
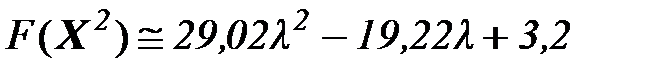
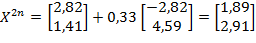
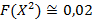
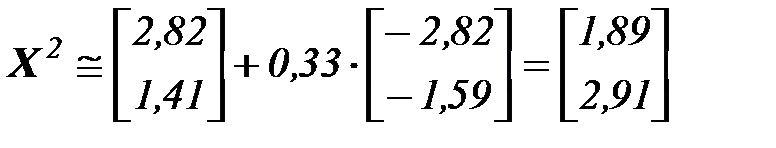
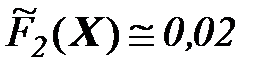
Вычисление продолжаются до тех пор, пока не выполнится критерий останова алгоритм.

Критерий останова:

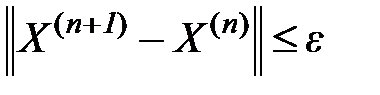(6)

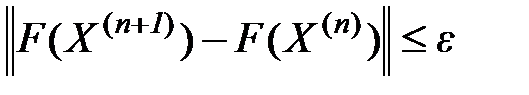(7)

Метод идеальной точки (алгоритм Франка-Вулфа)

12 Следующая ⇒

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.