
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Методы многокритериальной оптимизации
Методы многокритериальной оптимизации
I. Метод обобщённого скалярного критерия
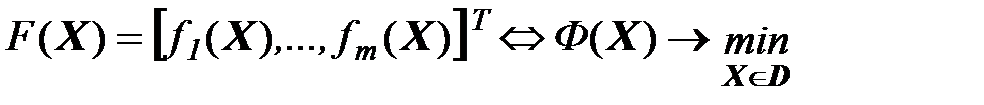
1. Линейная свертка: 
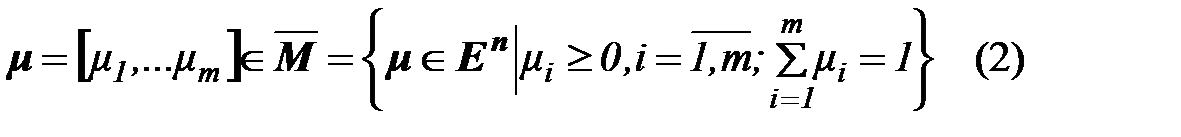
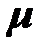 - вектор весовых коэффициентов
- вектор весовых коэффициентов
Если 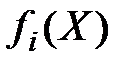 имеют различный физический смысл, то необходима нормализация критериев:
имеют различный физический смысл, то необходима нормализация критериев:
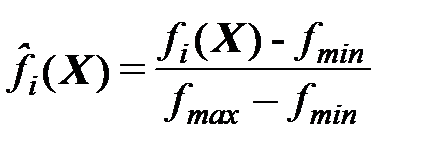
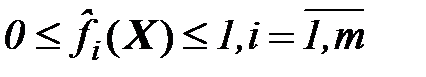
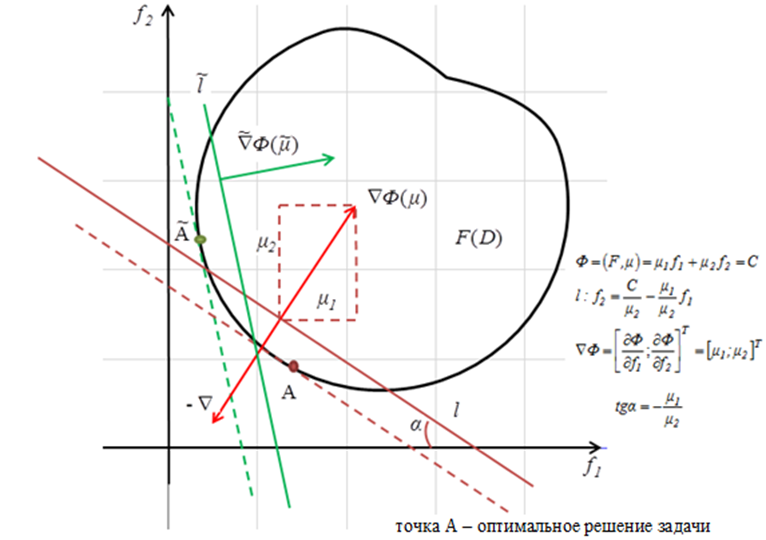
Геометрическая интерпретация
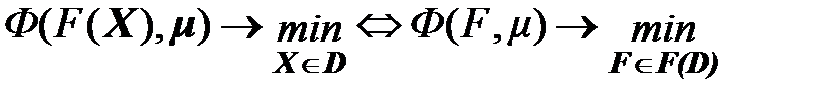
Пример 1. Решить задачу многокритериальной оптимизации методом линейной свертки
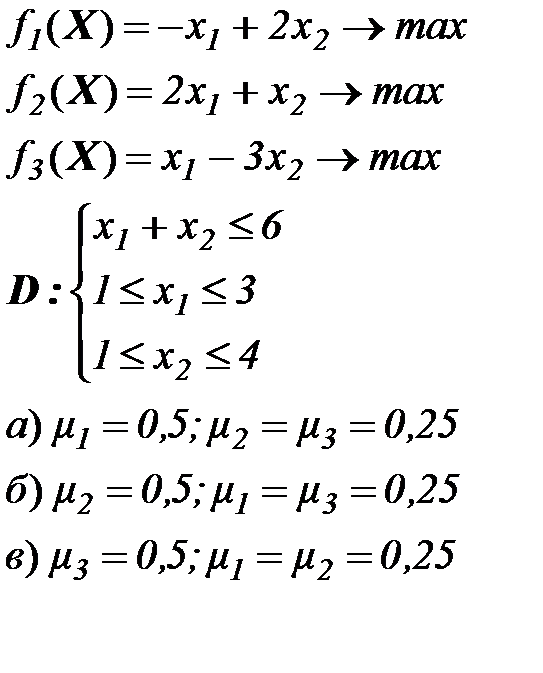
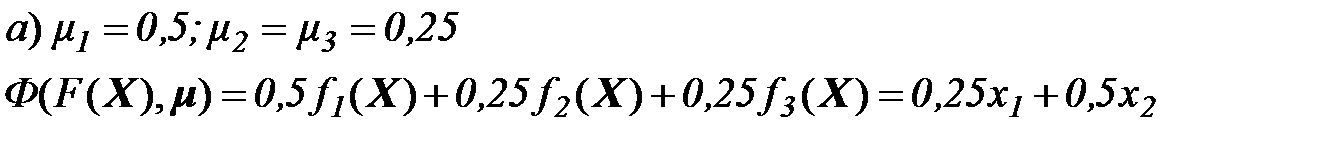
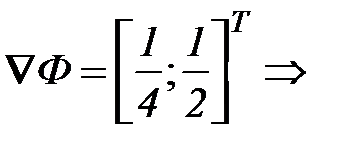 точка
точка 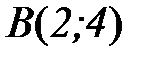 - оптимальное решение.
- оптимальное решение.
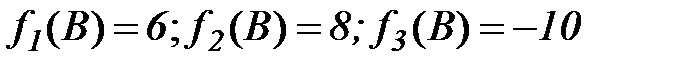
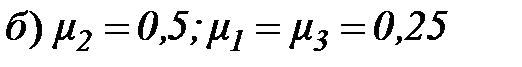
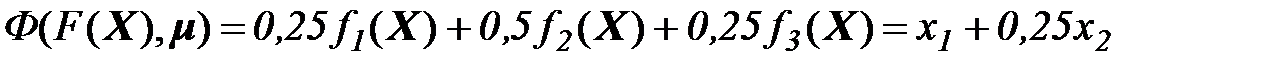
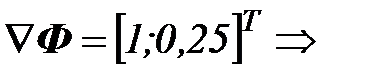 точка
точка 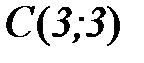 - оптимальное решение.
- оптимальное решение.
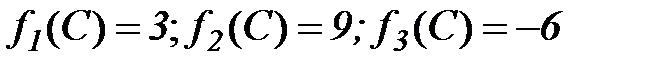
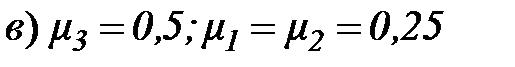
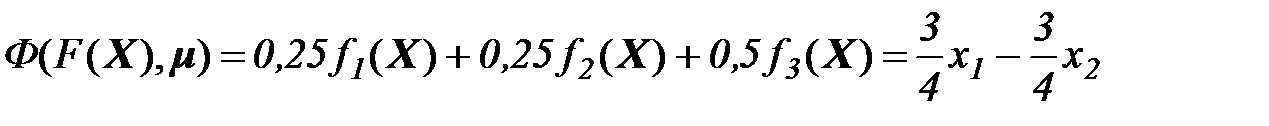
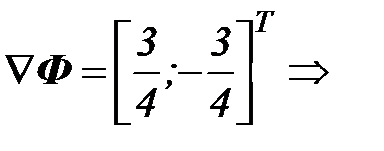 точка
точка 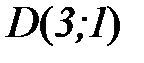 - оптимальное решение.
- оптимальное решение.
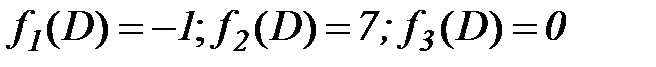
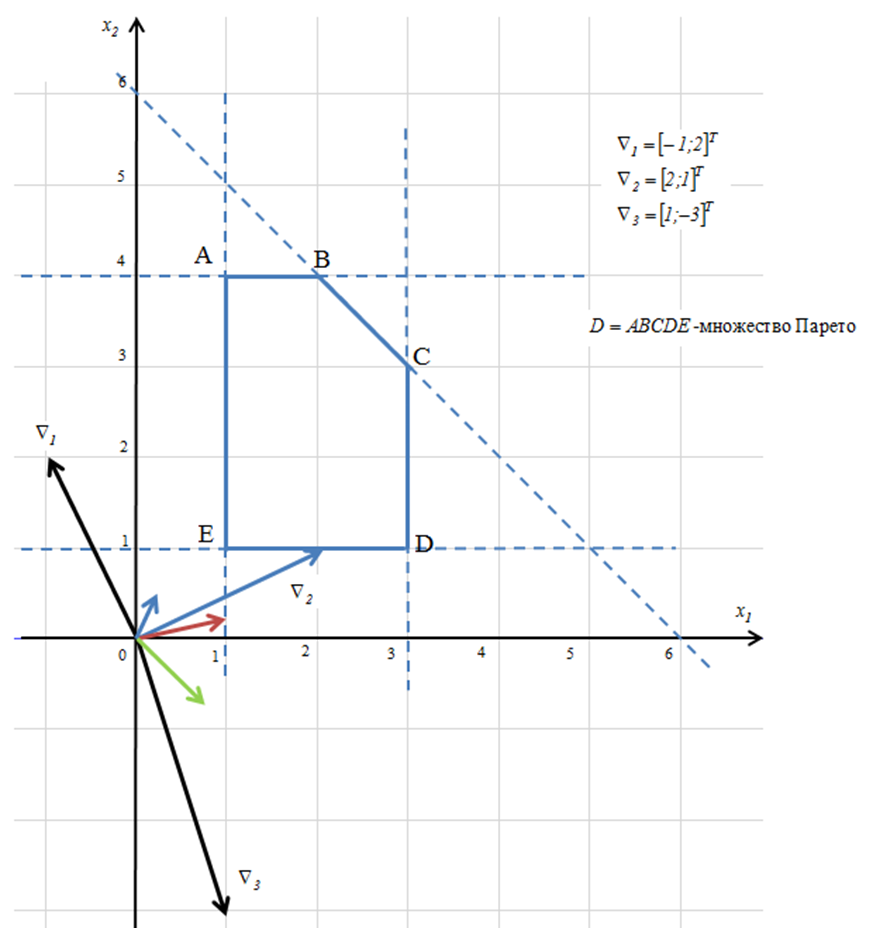
II. Методы, использующие информацию о желаемых уровнях значениях критериев
1. Пороговая оптимизация.
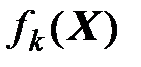 - основной критерий. На значения других критериев накладываем ограничения (пороги).
- основной критерий. На значения других критериев накладываем ограничения (пороги).
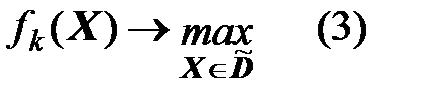
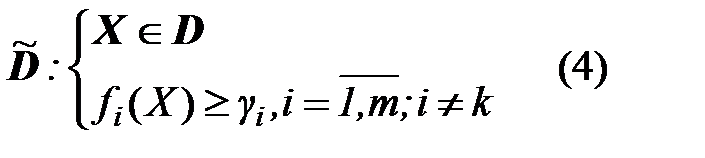
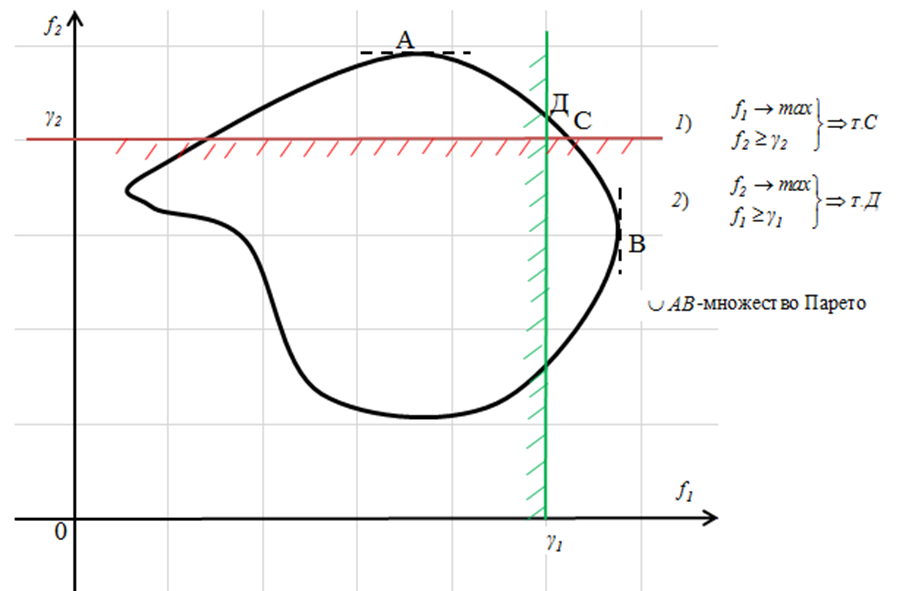
Пример 2. Решить задачу 1 методом пороговой оптимизации
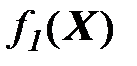 - основной критерий. Назначим пороговые значения на другие критерии:
- основной критерий. Назначим пороговые значения на другие критерии: 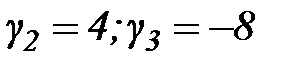 .
.
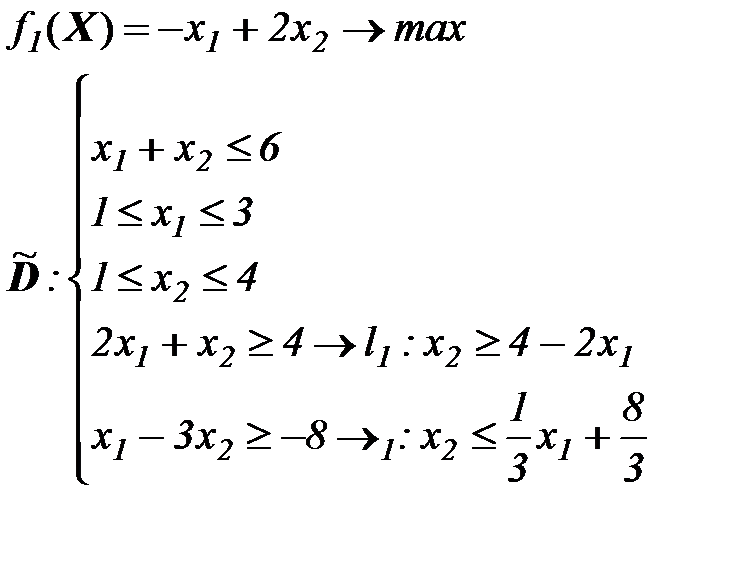
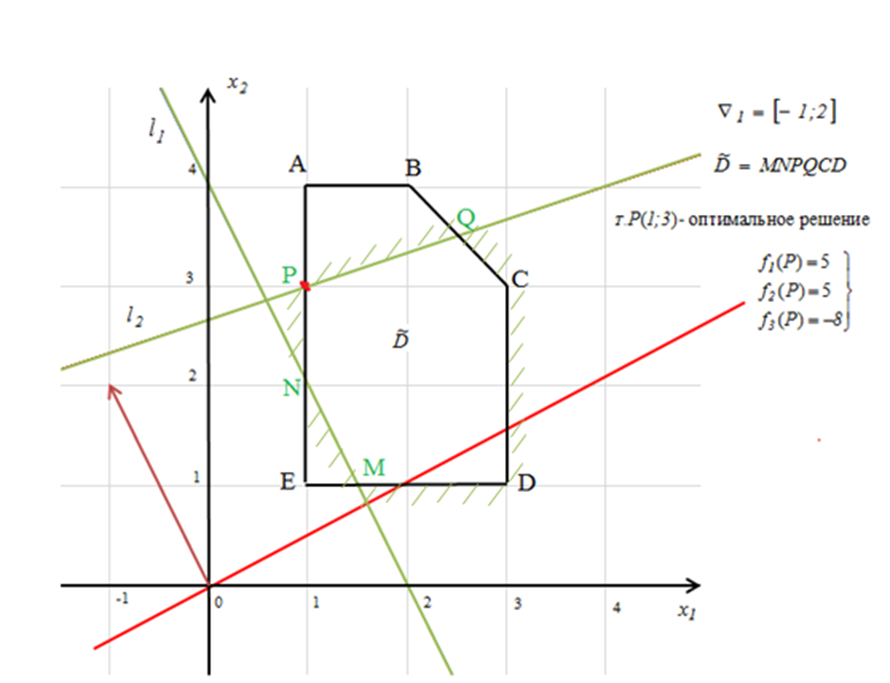
2. Метод идеальной точки.
А). 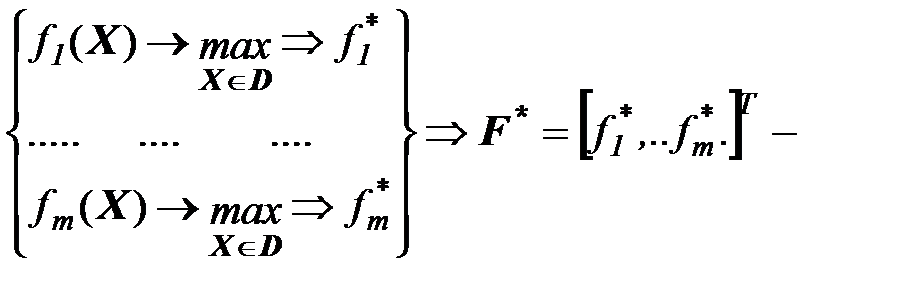 «идеальная» точка.
«идеальная» точка.
Б). Вводим метрику:
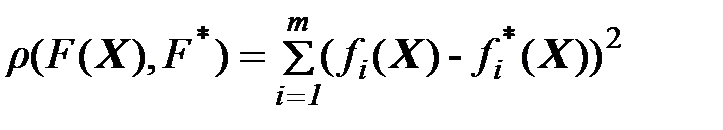
В). 
Геометрическая интерпретация
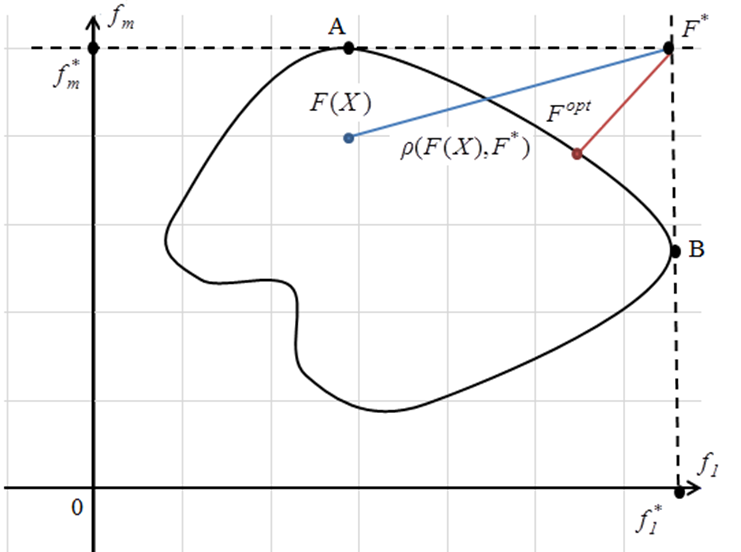
Пример 3. Решить задачу 1 методом «идеальной» точки
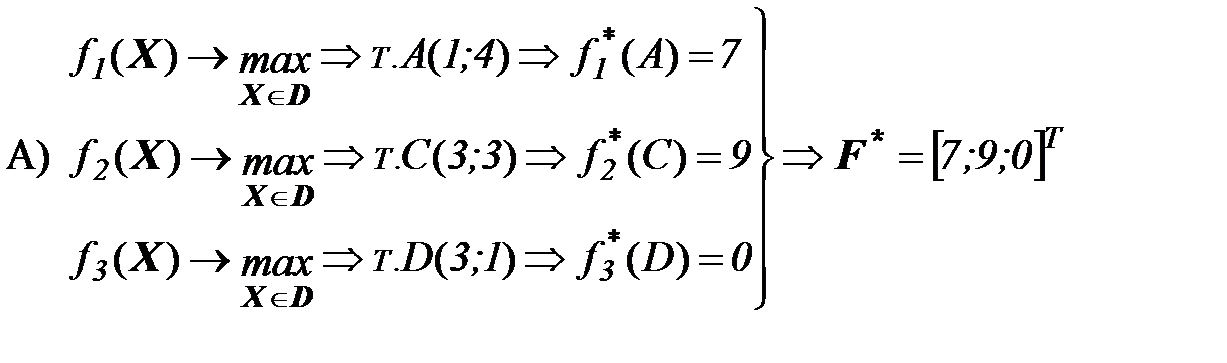
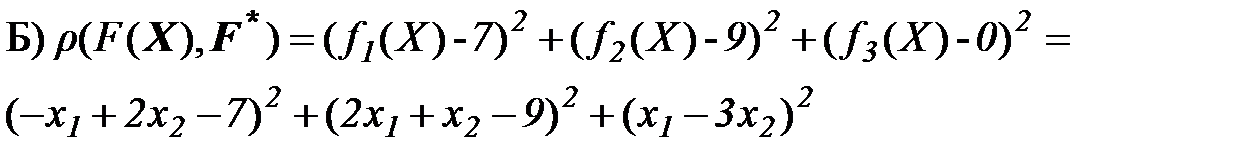
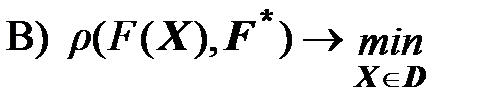

Для решения поставленной задачи был применен Франка-Вульфа, который будет рассмотрен на следующей лекции.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|