Кванттық механика

Кванттық механика

Таң дамалы тараулар

3-Тарау

Кванттық механиканың математикалық аппараттары

Сызық тық операторлар

Шредингер тең деуін шешкен кезде жү йенің толқ ындық функциясын жә не энергиясын табуғ а болады. Кейбір жағ дайларда бұ лардың мә ндері дискретті (потенциялдық шұ ң қ ырдағ ы бө лшек), басқ а кезде, мә ндері (бө гет арқ ылы ө тетін еркін бө лшек) ү здіксіз қ атар тү рінде болады.

толқ ындық функкцияны біле отырып, біз бө лшектің кең істіктің берілген нү ктесінде табылу ық тималдығ ын, сонымен қ атар, координаттарғ а тә уелді шамалардың орташа мә ндерін таба алар едік. Осы кезде бө лшектің координаттарын жә не импульсінің сә йкес проекцияларын белгілі мә ндерінің болатындығ ына душар болар едік. Бірақ, біз қ олданғ ан математикалық аппарат бірқ атар маң ызды мә селелерге жауап беруге жеткіліксіз еді. Мысал ү шін олардың кейбіреулерін келтіре кетейік. Дә л қ андай шамалардың мә ндерін бір мезгілде анық тауғ а болмайтын еді? Координаттардың функциясы болып табылмайтын орташа мә ндерін қ алай табуғ а болады? Координаттық механикалық жү йенің кү йін толық анық тау ү шін оның қ андай сипаттамаларын беру керек?

Кванттық механика мә селелерінің ерекше болмысы арнаулы математикалық аппаратты дамытуды жә не қ олдануды талап етті.

Кванттық механиканың математикалық аппараты кванттық механиканың мә селелерінің физикалық қ ойылуына сә йкес келуі тиіс. Ең тамашасы, математикада қ ажетті аппарат- сызық тық операторлар теориясы жасалып қ ойылғ ан екен. Біз ә уелі осы теорияның негіздерімен танысамыз, одан сызық тық операторлар теориясы аппаратының кванттық механиканың мә селелерімен қ андай байланыста екендігін кө рсетеміз.

Оператор деп біз, 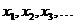айнымалылардың бір 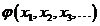функциясына осы айнымалылардың басқ а бір функциясы сә йкестендірілетін рецепт немесе ереже тү сініледі.

Алда біз операторларды шапкасы бар ә ріптермен белгілейтін боламыз, мысалғ а, . символдың кө мегімен функциядан 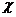функцияғ а ө ту ережесін

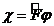(3. 1)

деп жазуғ а болады. Бірнеше қ арапайым операторларды қ арастырайық.

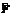оператор, мысалғ а, қ айсы-бір айнымалы бойынша дифференциалдауды білдіруі мү мкін

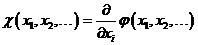Символдық тү рде бұ л операторды

деп белгілейді. Дифференциалдау операторлары жиірек кездеспейтін болады. Сондық тан біз олар ү шін дифференциалдық операторлардың арнаулы атауын енгіземіз. оператор қ андай да бір шамағ а кө бейтуді, дә режеге шығ аруды жә не т. б. білдіруі де мү мкін.

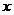тә уелсіз айнымалының операторын осы айнымалығ а кө бейту тү рінде анық таймыз

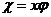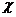жә не функциялар арасындағ ы интегралдық қ атынасты да операторлық тү рде беруге болады:

(3. 2)

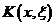функция интегралдық оператордың ядросы деп аталады.

Біз бұ рында да дифференциалдық операторлармен – оператормен, 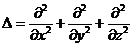Лаплас операторымен жә не басқ а да опраторлармн таныс болғ анбыз.

Енді біз сызық тық опраторды, ол ү шін

, (3. 3)

, (3. 4)

Тең діктер орындалатындай етіп, анық тайық, мұ нда 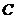-кезкелген тұ рақ ты. Осыдан,

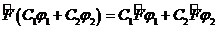(3. 5)

екендігі шығ ады, мұ ндағ ы 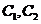–кез келген тұ рақ тылар. Жоғ арыда операторлар сызық тық опраторлар болып табылады, кванттық механикада біз тек сызық тық операторлармен ғ ана істес боламыз.

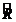Берілген жә не операторлармен олардың қ осындысын жә не кө бейтіндісін де анық тауғ а болады. жә не 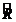опетаторлардың қ осындысы 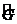оператор деп біз

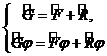(3. 6)

қ атынасымен боламыз. Анық талатын 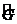операторды тү сінетін боламыз:

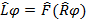(3. 7)

Егер ә уелі оператор қ олданылып, содан кейін 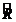оператор қ олданылатын болса, онда олардың кө бейтіндісі:

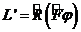(3. 8)

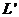жә не операторлары, жалпы алғ анда, бірдей емес, яғ ни операторлардың кө бейтіндісі кө бейткіштердің ретіне (тә ртібіне) тә уелді болады. Осығ ан сай, операторлардың алгебрасы – коммутирленбейтін шамалардың алгебрасы болып табылады. Егер операторлардың кө бейтіндісі олардың кө бейтілу ретіне тә уелсіз болса, онда оларды ө зара коммутирленетін дейді, кері жағ дайда куммутирленбейтін дейді. Мысал ретінде 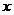бойнша дифференциалдау операторының 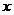-қ а кө бейту операторына кө бейтіндісін, кө бейтінділердің екі жағ дайында қ арастырамыз, яғ ни,

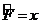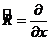
Кө бейтіндісінің операторы (1. 7) бойынша

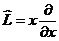
Енді 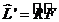операторды табамыз:

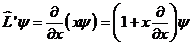
Кө ріп отырғ анымыздай, бұ л жағ дайда 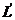оператор

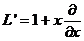
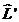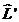оператормен бірдей емес. Сонымен, жә не операторлар коммутирленбейді. Енді жә не операторлар ү шін алынғ ан нә тижелерді пайдалана отырып,

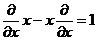
деп жаза аламыз.

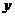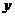Бұ л операторлық қ атынастағ ы бірді бірлік оператор деп атауғ а болады. Егер де біз оператор ретінде басқ а бір тә уелсіз айнымалығ а, мысалғ а, -ке кө бейту операторын алсақ, онда жә не операторлар коммутирленетін болып шығ ар еді:

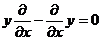(3. 9)

Кейбір операторлар ү шін

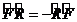(3. 10)

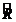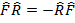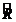қ атынасы орындалады. Бұ л жағ дайда жә не операторлар бұ л жағ дайда антикоммутирленетін деп аталады. операторды жә не операторларының коммутаторы деп атайды жә не 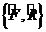жақ шамен белгіленеді:

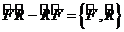(3. 11)

Берілген операторғ а 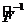кері операторды сә йкестеуге болады. Кері оператор

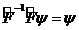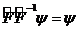
немесе

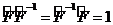(3. 12)

қ атынастармен анық талады. Егер қ айсы-бір оператор болса, онда оғ ан кері 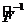оператор интегралдық оператор тү рінде болады. Шындығ ында да,

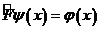(3. 13)

қ атынасы орындалсын. Сонда, осы тең діктің оң жә не сол жағ ына 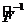оператормен ә сер ет отырып,

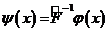(3. 14)

деп аламыз.

Екінші жазылғ ан (3. 14) қ атынасты

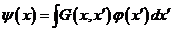(3. 15)

тү рінде жазуғ а болады, мұ нда 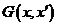функция (3. 13) тең деудің

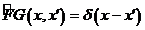(3. 16)

қ атынасын қ анағ аттандыратын Грин функциясы деп аталады. Шындығ ында да, егер біз (3. 15) тең діктің екі жағ ына да оператормен ә сер ететін болсақ, онда (3. 16) шарты кезінде біз қ айтадан (3. 13) қ атынасына келеміз. (3. 14) жә не (3. 15)-терді салыстыра отырып, 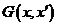Грин функциясының 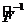интегралдық оператордың ядросы екендігіне келеміз. (3. 16) тең деуден 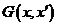Грин функциясы бірмә нділікпен анық талмайды. Бірмә нділікпен анық тау ү шін тағ ы да бір шекаралық шарттар тү ріндегі қ айсы-бір шарттарды беру керек.

(3. 13) қ атынасын, шешімі (3. 15) формуламен берілетін, 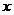берілген функциясы бар, 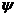функцияғ а қ атысты қ айсы-бір тең деу деп қ арастыруғ а болады. Тек мынаныескеру керек: жалпы шешімді алу ү шін біз (3. 15)-ке біртекті тең деудің жалпы шешімін қ осуымыз керек:

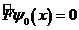
Сонда:

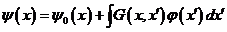(3. 17)

Алынғ ан қ атынас бізге алда қ ажет болады.

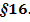Операторлардың меншікті мә ндері жә не меншікті функциялары

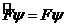(6. 1)

Операторлық қ атынасты қ арастырайық. (6. 1) қ атынас операторды қ олданғ ан кезде, қ айтадан қ андай да бір тұ рақ ты -қ а кө бейтілген функцияны аламыз. оператордың берілген тү рі кезінде, (6. 1) қ атынасты кез келген 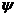функцияның қ анағ аттандырмайтыны анық. Басқ аша айтқ анда, (6. 1) қ атынас тең деу болып табылады. 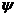функцияның тү рін (6. 1) тең деуді шешу арқ ылы табуғ а болады. Егер оператор сызық тық дифференциалдық оператор болып табылатын болса, онда (6. 1) тең деу дифференциалдық тең деу болып табылады. Тең деудің тү рінен бірден 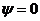-дің оның тривиал шешімі екендігі кө рінетіндіктен, (6. 1) сызық тық біртекті дифференциалдық тең деу болып табылады. Осында сызық тық біртекті дифференциалдық тең деулерді зерттеу, операторлар теориясының маң ызды мә селесі болып табылады. Бұ дан ә рі біз кез келген операторлар мен 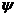функцияларды қ арастырамыз, тек белгілі шарттарды қ анағ аттандыратын функцияларды ғ ана қ арастыратын боламыз:

1) 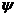функция тә уелсіз айнымалылардың ө згерістерінің тұ тастай облысында болуы керек. Мысалғ а, декарттық координаттар жағ дайында, 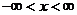, , 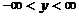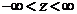облысында;

2) 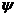функцияның болуы облысында, ол ө зінің бірінші туындысымен бірге, ерекше нү ктелерден басқ а жерлрден шектеулі жә не ү здісіз болуы қ ажет;

3) 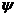функция бір мә нді болуы тиіс;

1)- 3) шарттар жиынтығ ын біз стандарттық шарттар деп атайтын боламыз. (6. 1) тең деуінің тривиалдық тан ө згеше жә не стандарттық шарттарды қ анағ аттандыратын шешімдерді параметрдің барлық мә ндері негізінде бола бермейді екен, тек оның кейбір таң далғ ан мә ндері кезінде ғ ана болады екен. (6. 1)-дің тривиалдық емес шешімдері болатын кездегі -тың мә ндері, оператордың меншікті мә ндері деп, ал оларғ а сә йкес келетін (6. 1)-дің шешімдері оператордың меншікті функциясы деп аталады.

Ең ә уелі ө зімізге белгілі, таныс болып қ алғ ан меншікті функциялар мен меншікті мә ндер жайлы есептерді сө з етейік.

1) Бө лшектің потенциялдық шұ ң қ ырдағ ы қ озғ алысын қ арастырғ ан кезде біз (16. 1) тең деуді 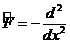дифференциалдық операторымен қ арастырдық. Шекаралық шарттар бізді оператордың (8. 5) меншікті мә ндеріне жә не (8. 7) меншікті функцияларына ә келді.

2) Егер біз оператордың сондай тү рі кезінде 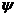-дің (0, 𝑙 ) аралық шекараларында нө лге тең болуын талап етсек, онда (8. 2) шешімінің тү рі 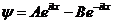болар еді. Егер 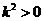болса, онда 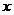-тың барлық мә ндері кезінде, 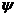функция шектеулі, сө йтіп, шешім стандарттық шарттарды қ анағ аттандырады. 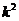теріс болатын кезде 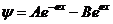, мұ нда 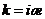, стандарттық шарттарды қ анағ аттандыратын шешімдер болмайды.

3) Осцилляторлар жайлы есепте біз 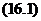шешімін 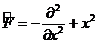операторы ү шін қ арастырдық ((10. 3)-ті қ ара). Есептің шешімі 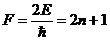, кезінде болады. Келтірілген мысалдардан кө ріп отырғ анымыздай, оператордың, біз оның спектрі деп атауғ а болатын, меншікті мә ндерінің жиынтығ ы дискреттік те (1 жә не 3 мысалдар), ү здіксіз (2-мысал) бола алады. Бірінші жағ дайда, спектрді дискреттік деп, екінші жағ дайда, ү здіксіз немесе тұ тас деп атайтын боламыз. Меншікті мә ндерінің тұ тас спектріне сә йкес келетін меншікті функциялар квадраттық интегралданады, яғ ни 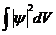интеграл жинақ ы болады. Меншікті мә ндердің тұ тас спектріне сә йкес келетін меншікті функциялар квадраттық интегралданбайды. Егер меншікті мә ндердің ә рбіреуіне тек жалғ ыз ғ ана 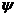меншікті функция сә йкес келетін болса, онда спектр ү стеленбеген деп аталады. Егер керісінше, бір ғ ана 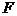меншікті мә нге бірнеше, мысалғ а, 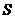меншікті мә ндер сә йкес келетін болса, онда қ арастырылып отырғ ан меншікті мә н 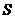еселенген деп аталады.

Келтірілген мысалдар біздің операторлар теориясына деген қ ызығ ушылық ты тудырады. Шредингер тең деуінің шешімдерін табу мә селесі белгілі тү рдегі операторлардың меншікті функциялар жайлы мә селенің дербес жағ дайы ғ ана болып табылады. Осы жерде ғ ана тоқ тап қ алмай, алғ а ұ мтылыс жасайық.

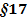. Эрмиттік операторлар

(16. 1) операторлық тең деудегі 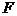меншікті мә ндердің, жалпы айтқ анда, комплекстік те болуы мү мкін. Бірақ, бізге қ ажеттісі тек заттық меншікті мә ндерге ә келетін тең деулер ғ ана болады. Меншікті мә ндері тек заттық қ ана болатын операторлар класы болады екен, олардың тек заттық меншікті мә ндері болады. Мұ ндай операторлар эрмиттік немесе ө здік тү йіндес деп аталады. Ә рбір сызық тық операторғ а басқ а бір 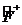операторды сә йкестеуге болады, оны біз берілген оператормен тү йіндес немесе эрмиттік тү йіндес деп атаймыз. Тү йіндес оператор

(17. 1)

шартымен анық талады. Бұ л жерде, ә деттегідей, жұ лдызша комплекс тү йіндестік шамаларды білдіреді. (17. 1)-де интегралдау тә уелсіз айнымалылардың бү кіл ө згерістері облысы бойынша жү ргізіледі. арқ ылы осы обылыстың элементі белгіленеді.

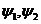функциялар (17. 1)-дегі интегралдардың жинақ ы болу талабын қ анағ аттандыруы тиіс. Сонымен қ атар солар кейбір интегралдық шарттарды қ анағ аттандыруы тиіс, олар кө біне 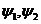функциялардың шексіздікте нө лге айналуы болып табылады. Егер оператор ө зінің тү йіндесімен бірдей тү сетін болса, яғ ни, 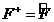, онда мұ ндай оператор эрмиттік немесе ө з-ө зіне тү йіндес деп аталады. Бұ л жағ дайда (17. 1)

(17. 2)

тү рін қ абылдайды, мұ ндағ ы

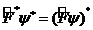
қ атынасымен анық талатын оператор.

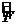оператор бастапқ ы операторғ а транспонирленген оператор деп аталады:

. (17. 3)

(17. 3)-ті (17. 1)-мен салыстыра отырып, 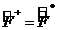деп аламыз. Тағ ы да мына қ атынастар орындалады:

, (17. 4)

. (17. 5)

. Эрмиттік операторлардың меншікті функцияларының ортогональдығ ы жә не нормалануы

Сызық тық эрмиттік оператордың тү рліш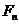е жә не 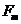меншікті мә ндеріне сә йкес келетін меншікті функциялары ө зара ортогональ болады, яғ ни

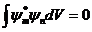
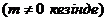(18. 1)

қ атынасын қ анағ аттандырады.

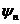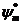Шындығ ында да, жә не функциялар (16. 1) тең деулерді қ анағ аттандырады

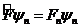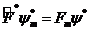, (18. 2)

оператор эрмиттік болатындық тан:

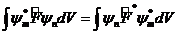(18. 3)

(18. 2) тең деуді пайдалана отырып, (18. 3) тең дікті

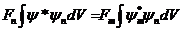
тү рінде жазамыз. Осыдан:

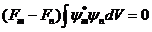. (18. 4)

Болжамдауымыз бойынша, 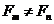болатындық тан,

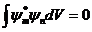(18. 5)

деп аламыз, бұ л біздің тоқ тамымызды дә лелдейді.

Алдағ ы жағ дайларды ескере отырып, дискретті спектрдің меншікті функцияларын

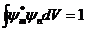(18. 6)

шартымен номалайтын боламыз, мұ ны бірге нормалау дейді.

(18. 1) жә не (18. 6) формулаларды

(18. 7)

деп біріктіреміз, мұ нда 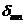-Кронекер символы:

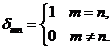
Бұ л жерде кванттық механикалық операторлардың тү рлерін теориялық негіздеуден гө рі оның практикалық қ олданылуының пайдалырақ екендігін ескере отырып, физикалық шамаларғ а сә йкестендірілген операторларды келтірейік:

1-кесте