
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема Множества и операции над ними
Тема " Множества и операции над ними"
Одними из основных, исходных понятий математики являются понятия множества и его элементов.
Множество состоит из элементов. Принадлежность элемента 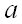 множеству
множеству 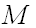 обозначается
обозначается 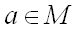 .
.
Множество может быть задано перечислением (то есть списком своих элементов), порождающей процедурой (то есть способом получения) или описанием характеристических свойств, которыми должны обладать его элементы.
Множество 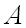 называют подмножеством множества
называют подмножеством множества 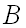 , если всякий элемент множества
, если всякий элемент множества 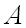 является элементом множества
является элементом множества 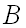 , обозначают
, обозначают 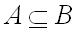 .
.
Если 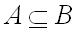 и
и 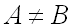 , то
, то 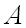 называют строгим или истинным подмножеством
называют строгим или истинным подмножеством 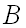 и обозначают
и обозначают 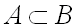 .
.
Множество, состоящее из конечного числа элементов, называют конечным.
Если число элементов множества бесконечно, то его называют бесконечным.
Число элементов в конечном множестве 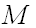 , называют мощностью
, называют мощностью 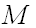 и обозначают
и обозначают 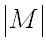 .
.
Множество мощности 0, то есть не содержащее элементов, называют пустым и обозначают 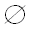 .
.
Принято считать, что пустое множество является подмножеством любого множества.
Операции над множествами
Объединением множеств 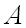 и
и 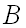 называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств
называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств 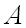 и
и 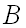 :
:
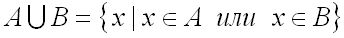 .
.
Пересечением множеств 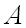 и
и 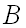 называется множество, состоящее из всех тех элементов, которые принадлежат и множеству
называется множество, состоящее из всех тех элементов, которые принадлежат и множеству 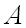 и множеству
и множеству 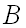 :
:
 .
.
Разностью множеств 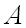 и
и 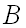 называется множество, состоящее из всех тех элементов множества
называется множество, состоящее из всех тех элементов множества 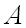 , которые не содержатся в множестве
, которые не содержатся в множестве 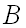 :
:
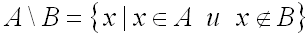 .
.
Прямым произведением 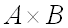 множеств
множеств 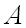 и
и 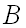 называется множество всех пар
называется множество всех пар 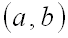 , таких, что
, таких, что 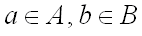 . В частности, если
. В частности, если 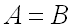 , то прямое произведение обозначается
, то прямое произведение обозначается 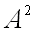 .
.
Для прямого произведения 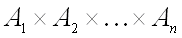 упорядоченный набор элементов
упорядоченный набор элементов 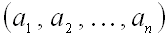 еще называют вектором,
еще называют вектором, 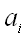 – его
– его 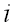 -ой компонентой (координатой), а
-ой компонентой (координатой), а 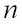 – длиной вектора.
– длиной вектора.
Теорема. Пусть 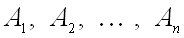 – конечные множества и
– конечные множества и 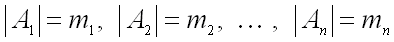 . Тогда мощность множества
. Тогда мощность множества 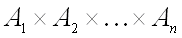 равна произведению мощностей множеств
равна произведению мощностей множеств 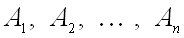 :
:
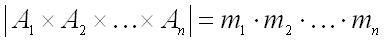 .
.
Проекцией 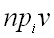 вектора
вектора 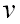 на
на 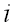 -ю ось называется его
-ю ось называется его 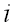 -я компонента (координата).
-я компонента (координата).
Пусть – множество 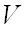 векторов одинаковой длины. Тогда проекцией множества
векторов одинаковой длины. Тогда проекцией множества 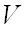 на
на 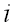 -ю ось называется множество проекций всех векторов из
-ю ось называется множество проекций всех векторов из 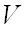 на
на 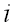 -ю ось:
-ю ось:
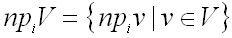 .
.
Соответствием между множествами 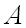 и
и 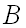 называется подмножество
называется подмножество 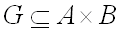 . Если
. Если 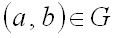 , то говорят, что
, то говорят, что 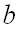 соответствует
соответствует 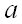 при соответствии
при соответствии 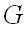 .
.
Множество 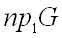 называется областью определения соответствия, множество
называется областью определения соответствия, множество 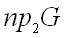 называется областью значений соответствия. Если
называется областью значений соответствия. Если 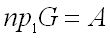 , то соответствие называют всюду определенным или полностью определенным.
, то соответствие называют всюду определенным или полностью определенным.
Множество всех 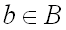 , соответствующих
, соответствующих 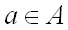 , называется образом
, называется образом 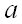 в
в 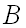 при соответствии
при соответствии 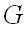 .
.
Множество всех 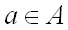 , которым соответствует
, которым соответствует 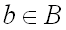 , называется прообразом
, называется прообразом 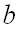 в
в 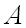 при соответствии
при соответствии 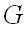 .
.
Соответствие называется функциональным, если образ любого элемента из 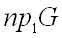 является единственный элемент из
является единственный элемент из 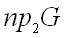 .
.
Функцией называется функциональное соответствие.
Если функция 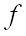 устанавливает соответствие между множествами
устанавливает соответствие между множествами 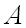 и
и 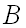 , то говорят, что функция имеет тип
, то говорят, что функция имеет тип  . Каждому элементу
. Каждому элементу 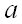 из своей области определения функция
из своей области определения функция 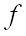 ставит в соответствие единственный элемент
ставит в соответствие единственный элемент 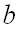 из области значений, это обозначают
из области значений, это обозначают 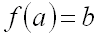 .
.

|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|