Существование сколь угодно высоких мощностей

Существование сколь угодно высоких мощностей

Теорема 1. Множество всех подмножеств непустого множества A имеет большую мощность, чем множество A.

Таким образом, если 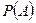- множество всех подмножеств множества A, то .

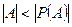Пример.

, .

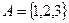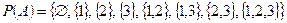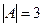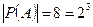Доказательство:

Пусть 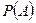- множество всех подмножеств непустого множества A. Так как множество одноэлементных подмножеств 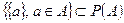эквивалентно множеству A ( 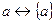), то .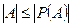

Докажем, что множество A не эквивалентно множеству 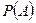. Будем доказывать от противного. Предположим, что A ~ 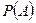. Тогда существует биекция .

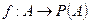Точку 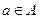будем называть точкой первого рода, если .

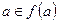Точку 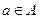будем называть точкой второго рода, если .

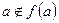Пусть 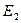- множество всех точек второго рода. Покажем, что 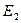не пусто. Пустое множество 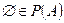. Так как 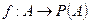- биекция, то существует точка 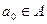, такая, что 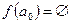, при этом 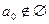. Таким образом, 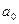- точка второго рода и множество 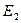не пусто.

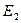является подмножеством множества A. Значит, 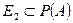. Так как f - биекция из A на 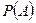, то существует точка 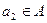, такая, что 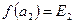. Какого рода точка ?

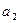Если 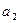- точка первого рода, т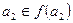о , но 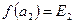- множество точек второго рода. Получили, что точка первого рода принадлежит множеству точек второго рода, чего быть не может.

Если 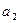- точка второго рода, т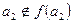о , но 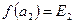- множество точек второго рода. Получили, что точка второго рода не принадлежит множеству точек второго рода, чего быть не может.

Таким образом, точка 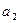не может быть ни точкой первого рода, ни точкой второго рода. Предположение неверно, следовательно, множество A не эквивалентно множеству 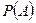. Отсюда 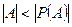. Теорема доказана.

Если A - непустое множество, то принято обозначение .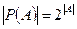

Теорема 2. Мощность множества всех подмножеств множества натуральных чисел равна c.

Доказательство:

Пусть 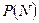- множество всех подмножеств множества N. Определим отображение 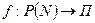, где П – множество всех последовательностей из 0 и 1.

Пусть 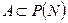, 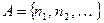. Тогда 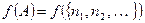есть последовательность, у которой единицы стоят на местах 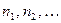, а на остальных местах нули.

Пример: ,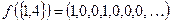

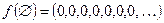
Очевидно, f - биекция. Следовательно, 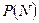~ П, но 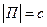, тогда .

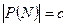Следствие. Мощность множества всех подмножеств всякого счётного множества равна c.

Доказательство: самостоятельно.

Ответ на вопрос, есть ли множества промежуточной мощности между 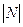и c, даёт континуум-гипотеза. Она была сформулирована Кантором в начале 80-х годов 19 века. Континуум-гипотеза состоит в том, что всякое бесконечное подмножество множества мощности континуума либо счётно, либо имеет мощность континуума.

Многочисленные попытки доказать континуум-гипотезу оказались безуспешными. Только в 1963 году Пол Джозеф Коэн установил, что континуум-гипотезу нельзя ни доказать, ни опровергнуть средствами самой теории множеств.