
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Предельные точки множества. Внутренние, внешние и граничные точки
Пусть M - метрическое пространство, E - какое-либо его подмножество.
Определение 1. Точка 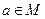 называется внутренней для множества E, если у неё существует окрестность
называется внутренней для множества E, если у неё существует окрестность 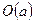 , целиком состоящая из точек множества E, т. е.
, целиком состоящая из точек множества E, т. е. 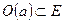 .
.
Определение 2. Внутренностью множества E в M называется множество всех внутренних точек множества E (обозначение < E> ).
Для любого множества E выполняется условие 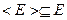 .
.
Определение 3. Точка 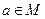 называется внешней для множества E, если у неё существует окрестность
называется внешней для множества E, если у неё существует окрестность 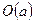 , не содержащая ни одной точки из множества E.
, не содержащая ни одной точки из множества E.
Определение 4. Точка 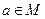 называется граничной для множества E, если в каждой её окрестности
называется граничной для множества E, если в каждой её окрестности 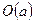 имеются как точки, принадлежащие множеству E, так и точки, не принадлежащие ему.
имеются как точки, принадлежащие множеству E, так и точки, не принадлежащие ему.
Определение 5. Множество всех граничных точек для множества E называется границей E и обозначается 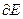 .
.
Как следует из этих определений, любая точка 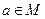 является для данного множества E либо внутренней, либо внешней, либо граничной, причём каждая из этих возможностей исключает две остальные. Множество E содержит все свои внутренние точки и не содержит внешних точек; граничные точки могут, как принадлежать, так и не принадлежать этому множеству.
является для данного множества E либо внутренней, либо внешней, либо граничной, причём каждая из этих возможностей исключает две остальные. Множество E содержит все свои внутренние точки и не содержит внешних точек; граничные точки могут, как принадлежать, так и не принадлежать этому множеству.
Определение 6. Точка 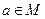 называется изолированной точкой множества E, если у неё существует окрестность
называется изолированной точкой множества E, если у неё существует окрестность 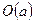 такая, что
такая, что 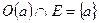 .
.
Определение 7. Точка 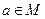 называется точкой прикосновения множества
называется точкой прикосновения множества 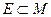 , если любая окрестность
, если любая окрестность 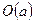 содержит, хотя бы одну точку множества E, т. е.
содержит, хотя бы одну точку множества E, т. е. 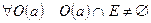 .
.
Определение 8. Точка 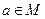 называется предельной точкой множества
называется предельной точкой множества 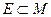 , если любая окрестность
, если любая окрестность 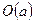 содержит, хотя бы одну точку множества E, отличную от точки a, т. е.
содержит, хотя бы одну точку множества E, отличную от точки a, т. е. 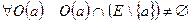 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|