Хелпикс

Главная

Контакты

Случайная статья



Тема: Межотраслевой баланс



Отраслевая матрица выпуска продукции

  Y X
А11 А12 А13 Y1 X1
А21 А22 А23 Y2 X2
А31 А32 А33 Y3 X3
Зарплата, млн. д. ед. P11 P12 P13    
% кредит P21 P22 P23    
Плата за природные ресурсы, млн. д. ед. P31 P32 P33    
Итого R1 R1 R1    

1, 2, 3 – номера отраслей

Аij – расход ресурсов каждой j-й отрасли для i-й отрасли, д. ед.

Хj – валовый выпуск продукции отрасли, д. ед.

Yj - конечная реализации отрасли, д. ед.

 

1) Рассчитать величины валового выпуска (Х)

Валовый выпуск: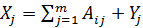

 

Х1 = А11 + А12 + А13 + Y1

Х2 = А21 + А22 + А23 + Y2

Х3 = А31 + А32 + А33 + Y3

 

2) Составить матрицу прямых затрат (А)

Матрица прямых затрат:

 

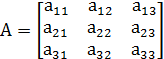, где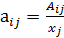

 

3) Рассчитать матрицу полных затрат (Е-А)-1

 

Поскольку

X = A X + Y →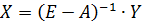

Порядок расчета матрицы полных затрат (Е-А)-1

а) Из единичной матрицы вычитаем матрицу прямых затрат

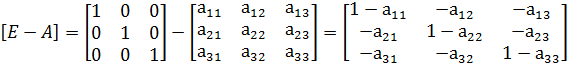
б) Полученную матрицу транспонируем:

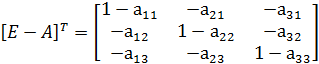
в) Находим матрицу, составленную из алгебраических дополнений, и делим на определитель:

 

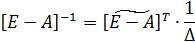
Определитель этой матрицы рассчитывается:

Δ = а11*а22*а33 + а12*а23*а31 + а13*а21*а32 - а13*а22*а31 - а12*а21*а33 - а11*а23*а32

 

 Алгебраические дополнения:

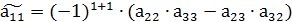
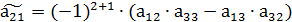
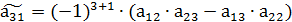 , и т. д.

 

4) Определить как изменится матрица Х, если конечная реализация во второй отрасли (У2) увеличится в 2 раза

5) Определить цены продукции в матричном виде (Ц)

 

→ ,

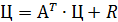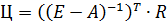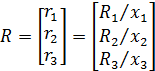
6) Рассчитать как изменятся цены при следующих условиях (для каждого условия отдельный расчет):

 - ЗП в 1й отрасли снизится в 1, 2 раза

- льготы по кредитам в 3й отрасли составят 5%

- плата за природные ресурсы возрастет во 2й отрасли на 150 д. ед.

 



  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.