Задание: изучить тему по плану и выполнить тест по закреплению темы.

Гр 204 Техническая механика Лепакова 13. 11. 21г

Тема урока: Изгиб.

Задание: изучить тему по плану и выполнить тест по закреплению темы.

План изучения темы:

1. Основные понятия и определения. Классификация видов изгиба.

2. Внутренние силовые факторы при прямом изгибе.

3. Эпюры поперечных сил изгибающих моментов.

4. Нормальные напряжения при изгибе.

5. Дифференциальные зависимости между изгибающим моментом, поперечной силой и интенсивностью распределенной нагрузки.

Тест по закреплению темы:

Выбрать один правильный ответ

1. Какие конструкции не рассчитывают на изгиб?

1. Балки.

2. Фермы.

3. Рамы.

4. Пластины.

2. Изгибающий момент считается положительным, если слева от сечения он направлен:

1. По ходу часовой стрелки?

2. Против хода часовой стрелки?

3. Поперечная сила считается положительной, если слева от сечения она действует:

1. Вниз?

2. Вверх?

4. Эпюры строят для нахождения опасных сечений?

1. да;

2. нет;

3. для определения законов изменения внутренних силовых факторов, напряжений и перемещений.

5. Что означает скачок на эпюре моментов?

1. изменение сечения;

2. наличие сосредоточенного момента;

3. приложение сосредоточенной силы.

6. Для двухопорной балки необходимо определить в начале реакции опор, а затем строить эпюры?

1. да;

2. нет;

3. это зависит от конструкции балки.

7. Знак изгибающего момента не зависит от внешних сил?

1. нет;

2. да;

3. при наличии сосредоточенного момента.

8. В поперечном сечении балки возникли изгибающий момент и поперечная сила. Укажите вид изгиба?

1. чистый изгиб;

2. поперечный изгиб.

9. В каких единицах измеряется осевой момент инерции сечения?

1. м⁴;

2. м³;

3. м².

10. Как называется внутренний силовой фактор, численно равный сумме поперечных внешних сил, приложенных к балке по одну сторону от рассматриваемого сечения?

1. осевая сила;

2. крутящий момент;

3. изгибающий момент;

4. поперечная сила.

11. Назовите внутренний силовой фактор, численно равный сумме моментов внешних сил, приложенных по одну сторону от рассматриваемого сечения относительно центра тяжести этого сечения.

1. осевая сила;

2. крутящий момент;

3. изгибающий момент;

4. поперечная сила.

12. Возникновением каких внутренних силовых факторов характеризуется прямой чистый изгиб?

1. М_изг;

2. М_изги Q;

3. Q;

4. нет правильного ответа.

13. Разделив изгибающий момент на осевой момент сопротивления, получим:

1. нормальное напряжение;

2. допускаемую силу;

3. момент инерции;

4. касательное напряжение

14. Какая геометрическая характеристика характеризует жесткость сечения при изгибе?

1. осевой момент сопротивления;

2. полярный момент сопротивления;

3. осевой момент инерции.

15. Какой вид деформации будет испытывать данная балка?

1. поперечный изгиб;

2. продольно-поперечный изгиб;

3. чистый изгиб;

4. косой изгиб.

Критерии оценивания:

Оценка «5» ставится, если обучающийся выполнил тест без ошибок;

Оценка «4» ставится, если обучающийся ответил правильно на 13-14 вопросов теста;

Оценка «3» ставится, если обучающийся ответил правильно на 11-12 вопросов теста;

Оценка «2» ставится, если обучающийся ответил правильно на 10 и меньше вопросов теста.

Учебник Сафонова Г. Г., Артюховская Т. Ю., Ермаков Д. А. Техническая механика, стр. 296-300

Электронная ссылка на учебник: znanium. com, labirint. ru

Электронные ресурсы: isopromat. ru, infourok. ru, prosopromat. ru

Ответы мне не присылать, проверю в тетради

Краткие теоретические и справочно-информационные материалы по теме:

Изгибом называется такой вид деформации бруса, при котором в его поперечных сечениях возникают изгибающие моменты.
Деформация изгиба заключается в искривлении продольной оси бруса.

Брус с прямой осью, подвергающийся изгибу, обычно называется балкой.

Если в сечениях балки возникает только изгибающий момент (поперечные силы отсутствуют), то изгиб называется чистым.

При изгибе одни слои балки растягиваются, а противоположные им – сжимаются, например:

Из балки нагруженной только изгибающим моментом

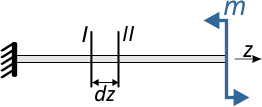
сечениями I и II мысленно вырежем фрагмент длиной dz

Как видно в данном случае верхние слои балки сжаты, а нижние – растянуты.

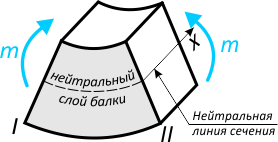
При этом наибольшему растяжению/сжатию подвержены крайние нижний и верхний слои балки.

Между ними расположен нейтральный слой, длина которого вследствие изгиба балки не изменяется.

Нейтральный слой расположен на уровне центров тяжести поперечных сечений балки, нормально к плоскости, в которой действуют изгибающие нагрузки.

Линия, образованная пересечением нейтрального слоя с поперечным сечением балки называется нейтральной линией сечения.

В общем случае плоского прямого изгиба в поперечных сечениях балки возникают два внутренних силовых фактора: изгибающий момент M и поперечная сила Q. Такой изгиб называется поперечным.

Для конкретизации направления внутренних усилий им присваиваются соответствующие индексы:

· M_x — момент, изгибающий относительно оси x (в плоскости yOz);

· Q_y — cила, направленная поперек балки вдоль оси y.

Плоский прямой (поперечный) изгиб возникает при действии на балку системы внешних сил, перпендикулярных к ее оси и лежащих в плоскости, проходящей через главную центральную ось сечения балки.

Изогнутая ось балки в этом случае – плоская кривая, совпадающая с плоскостью действия внешних сил.

Для определения внутренних силовых факторов Q и M используется метод сечений, суть которого применительно к балке показана на следующем рисунке:

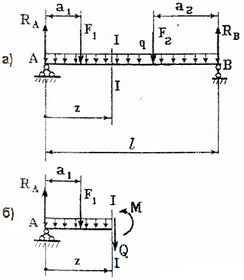
Рассматривая равновесие левой от сечения (I-I) части

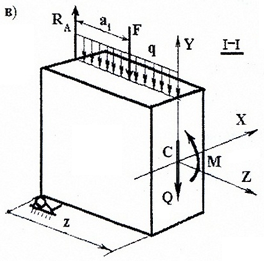
с учетом правила знаков для Q и M, запишем следующие уравнения равновесия:

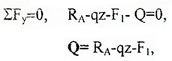
или в общем виде:

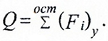
Внутренняя сила Q в поперечном сечении балки численно равна алгебраической сумме проекций на плоскость сечения всех внешних сил (активных и реактивных), действующих по одну сторону от рассматриваемого сечения.

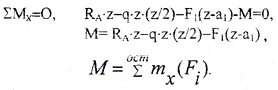
Изгибающий момент в поперечном сечении численно равен алгебраической сумме моментов внешних сил и пар, вычисленных относительно нейтральной оси рассматриваемого сечения и действующих по одну сторону от проведенного сечения.

Между изгибающим моментом M, поперечной силой Q и интенсивностью распределенной нагрузки q существуют следующие дифференциальные зависимости:

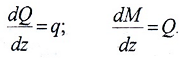
Эти формулы могут быть использованы при построении и проверке эпюр Q и M.

Графические изображения функций Q и M по длине балки называют эпюрами поперечных сил и изгибающих моментов.