Задание: изучить тему по плану, ответить на вопросы и решить задачу.

Гр 202 ОП. 02 «Техническая механика» на 09. 11. 21г

Тема урока: Расчеты на прочность по предельным состояниям.

Задание: изучить тему по плану, ответить на вопросы и решить задачу.

План изучения темы:

1. Расчеты на прочность по предельным состояниям.

2. Коэффициенты надежности по нагрузке, по материалу, по назначению и условиям работы.

3. Нормативные и расчетные нагрузки и сопротивления.

Вопросы:

1. Какие виды связей существуют?

2. Какая нагрузка называется распределенной; равнодействующей?

3. Что называется моментом силы относительно точки?

4. Проекция вектора силы на ось. Какое условие ее равенства нулю?

5. Метод сечения. Когда направления внутренних усилий положительные?

6. Что такое напряжение?

7. Какие условия прочности по предельным состояниям?

Учебник Сафонова Г. Г., Артюховская Т. Ю., Ермаков Д. А. Техническая механика, § 2. 2. 8

Электронная ссылка на учебник: znanium. com, labirint. ru

Электронные ресурсы: prosopromat. ru, interneturok. ru, soprotmat. ru

Посмотреть видеоурок: isopromat. ru

Ответы присылать мне на электронную почту: lepakova68@mail. ru или в ВК

Критерии оценивания:

Оценка «5» ставится, если обучающийся ответил на 7 вопросов в полном объёме и решил задачу без ошибок;

Оценка «4» ставится, если обучающийся ответил правильно в полном объеме на 7 вопросов и решил задачу с ошибками;

Оценка «3» ставится, если обучающийся ответил правильно в полном объеме на 7 вопросов;

Оценка «2» ставится, если обучающийся ответил на 6 и меньше вопросов.

Образец решения задачи:

Для деревянной балки прямоугольного поперечного сечения (рис. 7. 51, а) построим эпюры Q и Mz, определим высоту сечения h из условия прочности, приняв R = = 14 МПа, уу= 1, 4 и ус = 1, 0, и проверим прочность балки на скалывание по нейтральному слою, приняв RCK = 2, 4 МПа.

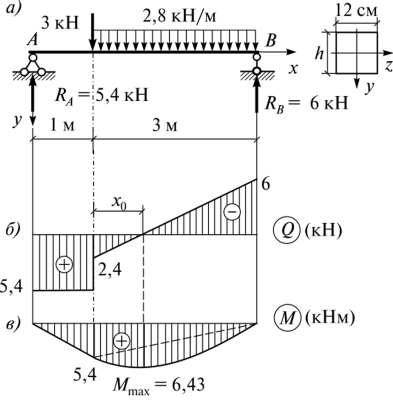
Рис. 7. 51

Определим опорные реакции:

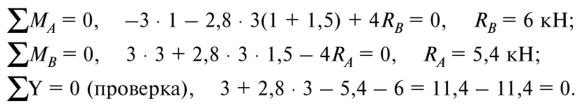
Вычислим значения Qv и Mz 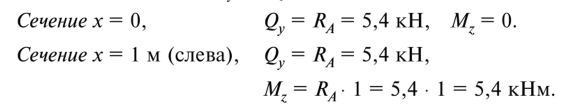в характерных сечениях балки.

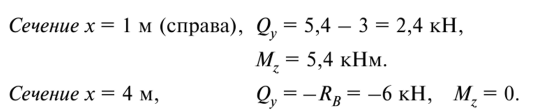
В пределах второго участка поперечная сила обращается в нуль. Положение этого сечения находим из подобия треугольников на эпюре Qy:

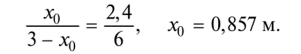
Вычислим экстремальное значение изгибающего момента в этом сечении:

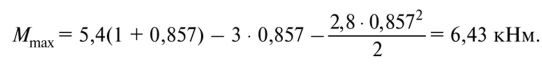
Эпюры Qy и Mz приведены на рис. 7. 51, б, в.

Опасным является сечение балки, где действует максимальный изгибающий момент. Вычислим расчетное значение изгибающего момента в этом сечении:

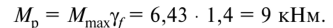
Требуемый момент сопротивления сечения

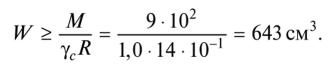
Выразим с помощью формулы момент сопротивления через высоту сечения h и приравняем его требуемому моменту сопротивления: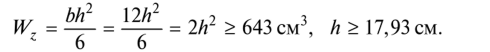

Принимаем прямоугольное сечение 12x18 см. Вычислим геометрические характеристики сечения:

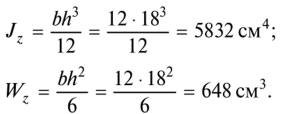
Определим наибольшие нормальные напряжения в опасном сечении балки и проверим ее прочность:

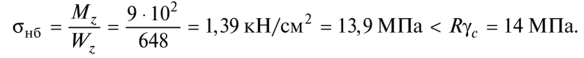
Условие прочности выполняется.

Задача для самостоятельного решения:

1. Выполнить расчет прочности стальной балки в поперечном сечении, указанном в задании на расчетной схеме.

Произвести полный расчет на прочность, построим эпюры Q и Mz, определим высоту сечения h из условия прочности, статически определимой деревянной двухопорной балки (рис. 1) при следующих данных: F=40кН, q=30 кН/м, a=0, 8 м, l=4м, допустимые нормальные и касательные напряжения: [σ ]=160 МПа и [τ ]=100 МПа, допустимый прогиб балки [f]=l/400, уу= 1, 4 и ус = 1, 0.

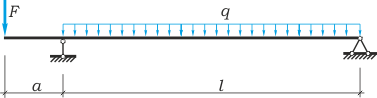
Ø Рис. 1

Краткие теоретические и справочно-информационные материалы по теме:

Расчет проходит по нормальным и касательным напряжениям, которые возникают из-за поперечной силы.
Касательные напряжения получаем по формуле Журавского и производим проверку с использованием главных напряжений по 3-ей теории прочности.
В онлайн расчет входят такие материалы, как сталь нескольких классов (С235, С245, С255, С345) и дерево трех сортов.
Также есть возможность выбора расчетной схемы: шарнир-шарнир, заделка-шарнир, заделка-заделка, свободный конец балки.
Коэффициенты поправки расчетного сопротивления дерева на изгиб приняты следующие:
Mдл = 0. 66 - совместное действие постоянной и кратковременной снеговой нагрузок
Mв = 0. 9 - нормальные условия эксплуатации дерева (влажность менее 12%)
Mт = 0. 8 - эксплуатация дерева при температуре 50 градусов
Mсс = 0. 9 - срок эксплуатации конструкции 75 лет

При расчете уже учитывается собственный вес конструкции.

Поперечная сила Q и изгибающий момент M в данном поперечном сечении балки являются соответственно главным вектором и главным моментом относительно центра тяжести сечения внутренних сил, действующих в рассматриваемом сечении. Поперечная сила численно равна сумме проекций на нормаль к оси балки (на ось y) этих сил, а изгибающий момент – сумме моментов тех же сил относительно центра тяжести сечения. Для левой отделенной части балки считаются положительными: поперечная сила, если направлена вниз; изгибающий момент, если стремится вращать рассматриваемую часть против хода часовой стрелки. Для правой отделенной части балки правила знаков для Q и M – противоположные. Можно пользоваться также следующим правилом: поперечная сила считается положительной, если она стремится повернуть прилегающий к рассматриваемому сечению участок балки по часовой стрелке; изгибающий момент считается положительным, если он вызывает растяжение нижних волокон балки. Построение эпюр выполняется по участкам загружения, в пределах которых не появляются новые сосредоточенные нагрузки и не заканчиваются, и не претерпевают изменение действующие распределенные нагрузки, вследствие чего аналитические выражения для функций Q(x) и M(x) не меняются. Эпюры вычерчиваются с указанием масштаба под расчетной схемой балки. Положительные значения поперечной силы откладываются от базовой линии вверх, изгибающего момента – вниз. На эпюре Q проставляется знак плюс на участках, расположенных выше базовой линии, и знак минус на участках ниже базовой линии; на эпюре M – наоборот. При линейных функциях M(x) и Q(x) вычисляются их значения на концах участков загружения, для нелинейных выражений M(x) и Q(x) – на концах и в середине участков загружения. Кроме того, находятся сечения, в которых поперечная сила обращается в нуль, и приводятся значения M в этих сечениях.

Расчет прочности выполняют в сечении, указанном в задании на расчетной схеме балки. В рассматриваемом сечении находят величины Q и M. При высоте балки h идеализированный двутавр, представляющий собой совокупность прямоугольных элементов – полок шириной b и толщиной t и стенки высотой (h–2t) и толщиной s.

Опоры обозначены буквами A и B. Поместим начало координат в точку A. Перед составлением уравнений равновесия необходимо выбрать направления реакций и показать их на расчетной схеме. Если в результате вычислений какая-либо реакция получится отрицательной, значит ее направление противоположно выбранному. В этом случае следует на расчетной схеме изменить ее направление на обратное и в дальнейшем считать эту реакцию положительной. Если на балку действует распределенная нагрузка, то для определения реакций опор ее заменяют равнодействующей, которая равна площади эпюры нагрузки и приложена в центре тяжести этой эпюры. Три неизвестных реакции опор определим из уравнений равновесия. Поскольку все внешние нагрузки перпендикулярны оси балки (распор отсутствует), сумма проекций всех сил на ось Z равна нулю и HA = 0. q P C Z Y A B HA a L 4 Сумма моментов всех сил относительно опорного шарнира A равна нулю Σ MA = 0. Составляя уравнение равновесия, находим опорную реакцию RB. Аналогично сумма моментов относительно опоры B – Σ MB = 0 откуда находится реакция опоры A.

Проверка правильности определения реакций может быть осуществлена путем использования условия равенства нулю суммы проекций всех сил на вертикальную ось Σ Υ = 0 или условия равенства нулю суммы моментов относительно любой точки C, отличной от A и B, т. е. Σ MC = 0.