Контакты

Случайная статья

Дифференциальные уравнения второго порядка

Дифференциальные уравнения второго порядка

Дифференциальные уравнения II порядка - уравнения, которые содержат производные или дифференциалы II порядка. Решение таких уравнений сводится к двукратному интегрированию.

Алгоритм решение уравнения у//= f(x).

1. Записать уравнение в виде: 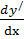= f(x).

2. Разделить переменные: 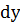^/= f(x)dx.

3. Проинтегрировать обе части уравнения: 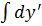= 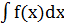, y^/= F₁(x)+c₁.

4. Записать уравнение, расписав производную через дифференциалы: 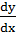= F₁(x)+c₁. 5. Разделить переменные: 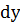= (F₁(x)+c₁)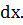

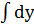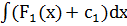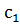6. Проинтегрировать обе части уравнения: = , у= + х+с₂.

Пример. Решите дифференциальное уравнение II порядка: у//=4х.

1. Записать уравнение в виде: = 4х

2. Разделить переменные: 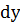^/= 4хdx

3. Проинтегрировать обе части уравнения: 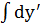= , y^/= 2х²+ c₁

4. Записать уравнение, расписав производную через дифференциалы: 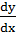= 2х²+ c₁

5. Разделить переменные: 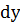= (2х²+ c₁)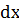

6. Проинтегрировать обе части уравнения: 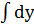= 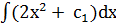, у= 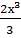+с₁х+с₂.

Решите дифференциальные уравнения:

1. у^//= 18х+2

2. у^//= х³

3. у^//= 0

4. у^//= 2 -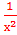

5. у^//-е^х+2 =0

Решите задачу Коши для дифференциальных уравнений:

1. е^-х у^//= 39 (х=0, у=2, у^/=1)

2. 10у^//-5= х²(у^/= , х=0, у= )

3. 5у^//-cosx=x (х=0, у=-2, у^/=-1)

4. у^//=2х³+5х (х=0, у=1, у^/=2)

5. у^//= 1- 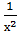(у=-1, х=1, у^/=1)

Таблица интегралов.

1. Повторите материал по теме.

2. Решите задания на решение задачи Коши 1-3.

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.