
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Практическая работа. Тема: Основные теоремы о пределах. Первый и второй замечательные пределы. Вычисление пределов на бесконечности и в точке. Краткие теоретические сведения по теме
Практическая работа
Тема: Основные теоремы о пределах. Первый и второй замечательные пределы. Вычисление пределов на бесконечности и в точке
Цель работы: учиться вычислять пределы функций в точке и на бесконечности и в точке
В результате выполнения практической работы обучающийся
должен знать: понятия и методы вычисления предела функции в точке, на бесконечности;
должен уметь: применять методы вычисления предела функции в точке, на бесконечности, раскрывать неопределенности вида  .
.
Форма проведения работы: практикум.
Краткие теоретические сведения по теме
Предел функции 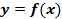 в точке
в точке 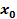 ‑ это величина
‑ это величина 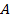 (конечная или бесконечная), к которой стремится значение функции
(конечная или бесконечная), к которой стремится значение функции 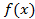 если аргумент функции
если аргумент функции 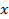 стремится к данному числу
стремится к данному числу  .
.
Обозначение: 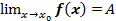 .
.
Если функция 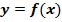 непрерывна в точке
непрерывна в точке  , то
, то 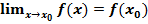
Пример 1: Найти предел функции 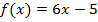 в точке
в точке 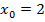 .
.
Решение. Запишем предел функции 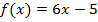 в точке
в точке 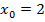 :
: 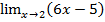 . Чтобы найти этот предел подставим вместо переменной
. Чтобы найти этот предел подставим вместо переменной 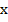 число 2, получим:
число 2, получим: 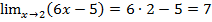 .
.
Пример 2: Вычислить  .
.
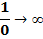
|
Решение. Подставим вместо переменной 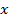 число -8, получим:
число -8, получим:  .
.
Предел функции 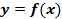 на
на 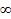 ‑ это величина
‑ это величина 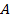 (конечная или бесконечная), к которой стремится значение функции
(конечная или бесконечная), к которой стремится значение функции 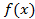 если аргумент функции
если аргумент функции 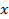 стремится к
стремится к 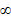 .
.
Обозначение: 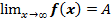 .
.
Пример 3: Вычислить 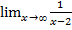 .
.
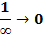
|
Решение. В функцию вместо 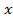 подставим
подставим 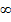 , получим:
, получим: 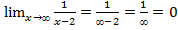 .
.
Для раскрытия неопределенности вида  необходимо разделить числитель и знаменатель дроби на наивысшую степень числителя или знаменателя.
необходимо разделить числитель и знаменатель дроби на наивысшую степень числителя или знаменателя.
Пример 4: Вычислите 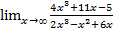 .
.
Решение. В функцию вместо 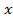 подставим
подставим 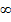 , получим неопределенность
, получим неопределенность  . Для раскрытия такой неопределенности разделим числитель и знаменатель дроби на наивысшую степень числителя или знаменателя, т. е. на
. Для раскрытия такой неопределенности разделим числитель и знаменатель дроби на наивысшую степень числителя или знаменателя, т. е. на 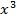 , получим:
, получим:
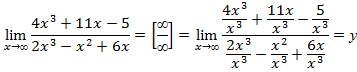
сократим каждую дробь и вновь вместо 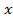 подставим
подставим 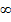 , получим
, получим
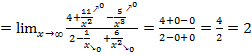 .
.
Пример 5: Вычислите предел функции  при
при 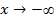 и
и 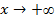 .
.
Решение. Запишем предел функции 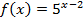 при
при 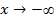 :
: 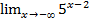 .
.
Чтобы найти этот предел вместо переменной 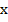 подставим
подставим 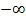 , получим:
, получим:
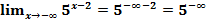 =
=
Применим свойство степеней 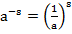 , получим
, получим 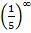 . Делаем вывод, что степень при бесконечном увеличении показателя приближается к бесконечно малому значению, т. е. стремится к 0:
. Делаем вывод, что степень при бесконечном увеличении показателя приближается к бесконечно малому значению, т. е. стремится к 0:
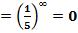 .
.
Теперь запишем предел функции 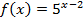 при
при 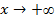 :
: 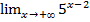 .
.
Чтобы найти этот предел вместо переменной 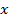 подставим
подставим  , получим:
, получим:
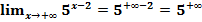 =
=
Делаем вывод, что при бесконечном увеличении показателя степень 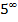 бесконечно увеличивается, т. е. стремится к
бесконечно увеличивается, т. е. стремится к 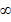 :
:
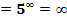 .
.
Задания на практическую работу:
1. Вычислить пределы функций в точке:
а)  ; в)
; в) 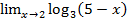 ; д)
; д) 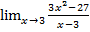 ;
;
б) 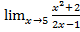 ; г)
; г) 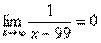 и)
и) 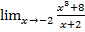 .
.
2. Вычислить пределы функций на бесконечности:
а) 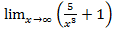 ; в)
; в) 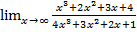 ; д)
; д) 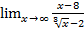 ;
;
ж) 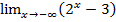 ;
;
б) 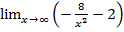 ; г)
; г) 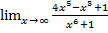 ; е)
; е) 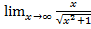 ; з)
; з) 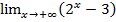 .
.
Контрольные вопросы:
1. Что называют пределом функции в точке?
2. Как вычислить предел функции в точке?
3. Что называют пределом функции на бесконечности?
4. Как раскрыть неопределенность вида  ?
?
5. Чему равен предел отношения константы к бесконечно большой величине?
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|