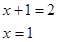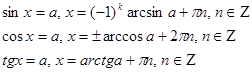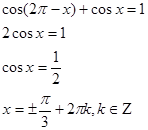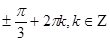- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Математика. Метод замены уравнения равносильным.. Теоремы равносильности. Пример.
Математика
ПР№11 Общие методы решений тригонометрических уравнений.
Решите уравнения все -получите «5»
Долгожданную троечку можно получить за правильно решенные три первых примера.
Основная литература: «Математика» 11 класс: учебник для общеобразовательных учреждений (базовый уровень) /А. Г. Мордкович.
| I вариант | IV вариант |
1) 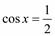 ; 2) ; 2) 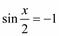 ;
3) ;
3) 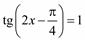 ;
4) ;
4) 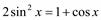 ;
5) ;
5) 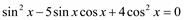 ;
6) ;
6) 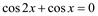 . .
| 1) 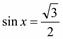 ; 2) ; 2) 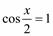 ;
3) ;
3) 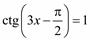 ;
4) ;
4) 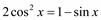 ;
5) ;
5) 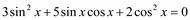 ;
6) ;
6) 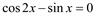 . .
|
| 1 вариант | 2 вариант |
| 1 Беднягин 2 Беднягин 3 Богданов 4 Ваулин 5 Воронин 6 Гуляев 7 Домолоков 8 Заварин 9 Злотник 10 Каренин 11 Колчин | 12 Корнилов 13 Костюченко 14 Кузнецов 15 Матковский 16 Мухачев 17 Никитин 18 Николаев 19 Припутнев 20 Романов 21 Сенатов 23 Чунин 24 Кутищев 25 Мамедов |
Решение.
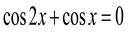
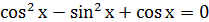
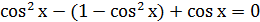
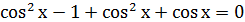
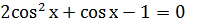
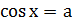
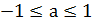
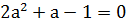

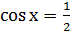
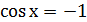
Найдите переменную самостоятельно и запишите ответ.
|
Метод замены уравнения равносильным. | ||
| Показательные уравнения | Логарифмические уравнения | Тригонометрические уравнения |
|
Теоремы равносильности Два уравнения называются равносильными, если множества их корней совпадают (в том числе, уравнения, не имеющие корней, считаются равносильными). Теорема 1. Если любое выражение, входящее в уравнение, заменить тождественно равным ему на области определения уравнения выражением, то получим уравнение, равносильное данному. Теорема 2. Если к обеим частям уравнения прибавить выражение, имеющее смысл на области определения уравнения, то получим уравнение, равносильное данному. Следствие. Если любое слагаемое перенести из одной части уравнения в другую, поменяв его знак на противоположный, то получим уравнение, равносильное данному. Теорема 3. Если обе части уравнения умножить (разделить) на выражение, имеющее смысл и отличное от нуля на области определения уравнения, то получим уравнение, равносильное данному. | ||
| Уравнение равносильно f(x) = g(x).
Пример. Уравнение
Ответ. 1 | Уравнение 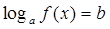 равносильно уравнению
равносильно уравнению
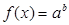 , где , где 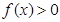 Пример.
Уравнение
Пример.
Уравнение 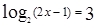 равносильно уравнению равносильно уравнению 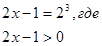
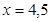 Ответ. 4, 5
Ответ. 4, 5
| Тригонометрические уравнения, решаемые с помощью тригонометрических формул, сводятся к одному из нескольких типов, решаемые стандартными методами. Пример. Ответ.
|
Уравнение loga f(x) = loga g(x)
(f(x) > 0, g(x)> 0, a> 0, a≠ 1)
равносильно f (x) = g(x).
Пример.
 Проверка.
Проверка. 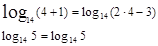 Ответ. 4
Ответ. 4
| ||
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|
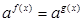 (a > 0, a≠ 1)
(a > 0, a≠ 1)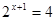 преобразуем в уравнение равносильно уравнению
преобразуем в уравнение равносильно уравнению