
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Дисциплина – Математика
ФИО преподавателя Мисюк Татьяна Максимовна
электронная почта musik@inbox. ru
| Группа | Дата занятия | Тема | Срок сдачи | Форма контроля |
| Б-21 | 20 ноября | Самостоятельная работа № 5. Тема: Вычисление площади плоской фигуры, длины кривой, объёма и площади тел вращения | 22 ноября | Решение задач |

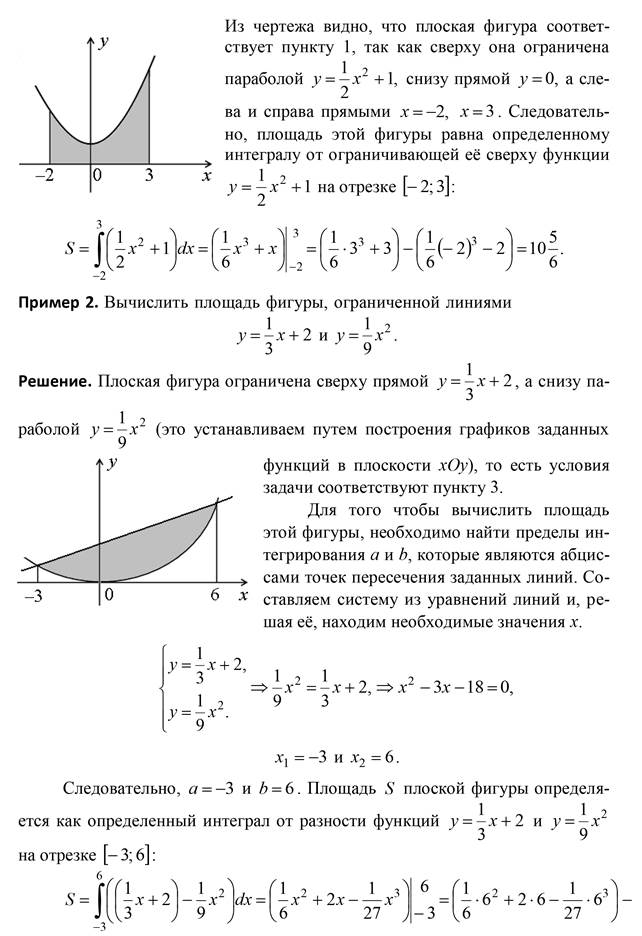

Пример 3. Вычислите площадь фигуры, ограниченной линиями:
а) 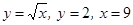 ; б)
; б) 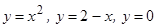 .
.
| № | План вычисления площади криволинейной трапеции | Применение плана | |
| шага | а) 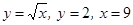
| б) 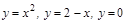
| |
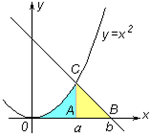
| Строим заданные линии и штриховкой отмечаем фигуру, площадь которой надо найти. Установим, является ли эта фигура криволинейной трапецией | 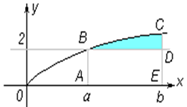
| 
| |
| Записываем формулу для вычисления площади искомой фигуры | 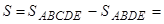
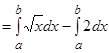
| 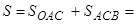
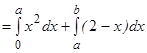
| |
| Находим пределы интегрирования | 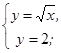 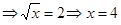 , ,
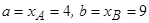
| 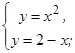 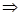 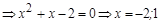
| |
| Вычисляем искомую площадь по формуле (*) | 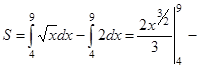
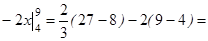 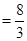 , ,
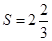 (кв. ед. ) (кв. ед. )
| 
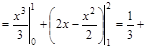
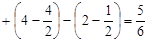 , ,
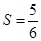 (кв. ед. ) (кв. ед. )
| |
Пример 4. 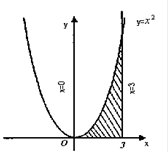 Определить площадь S фигуры, заключённой между ветвью кривой y = x2, осью OX и прямыми x = 0, x = 3.
Определить площадь S фигуры, заключённой между ветвью кривой y = x2, осью OX и прямыми x = 0, x = 3.
Решение: 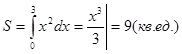
Пример 5. Найти площадь S фигуры, заключённой между осью OX и кривой y = x2 – 4x.
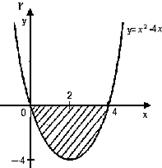
| Решение: рассмотрим точки пересечения кривой y = x2 – 4x с осью Oх:
y = 0; 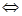 x2 – 4x = 0 x2 – 4x = 0 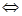 x ( x – 4 ) = 0; x ( x – 4 ) = 0; 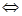 x1 = 0 или x2 = 4.
Найдём производную функции x1 = 0 или x2 = 4.
Найдём производную функции 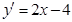 , и точки экстремума: , и точки экстремума:
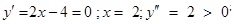 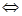 x = 2 – точка min,
y(2) = - 4.
Искомая площадь ограничена сверху осью OX, снизу графиком функции y = x2 – 4x, слева прямой x = 0, справа прямой x = 4. Так как на отрезке x = 2 – точка min,
y(2) = - 4.
Искомая площадь ограничена сверху осью OX, снизу графиком функции y = x2 – 4x, слева прямой x = 0, справа прямой x = 4. Так как на отрезке 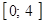 y < 0, то y < 0, то
|
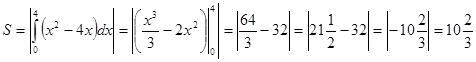 (кв. ед. )
(кв. ед. )
Пример 6. Найти площадь фигуры, заключённой между линиями y = x3, x=-1, x=2 и осью OX.
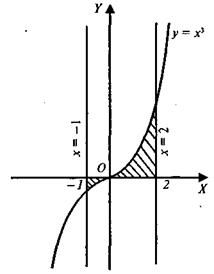
| Решение: найдем точки пересечения графика функции 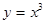 с осью ОХ:
y = x3; y = 0 с осью ОХ:
y = x3; y = 0 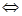 x = 0; Вычислим производную функции: y’ = 3x2; y’ = 0 x = 0; Вычислим производную функции: y’ = 3x2; y’ = 0 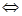 x = 0 . Найдем значение второй производной в точке х=0: y” = 6x; y” (0) = 0. Вычислим y”(-1) = -=6; y”(1) = 6; x = 0 . Найдем значение второй производной в точке х=0: y” = 6x; y” (0) = 0. Вычислим y”(-1) = -=6; y”(1) = 6; 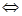 Т. к. y” меняет знак при переходе через х =0 Т. к. y” меняет знак при переходе через х =0 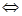 т. (0; 0) – точка перегиба. Искомая площадь состоит из двух частей, поэтому: т. (0; 0) – точка перегиба. Искомая площадь состоит из двух частей, поэтому:
|
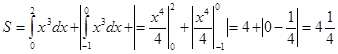 (кв. ед. )
(кв. ед. )
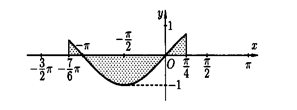
Пример 7. Найти площадь фигуры ограниченной кривой 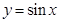 , прямыми
, прямыми 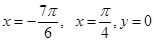
Решение: Построим график функции
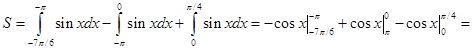
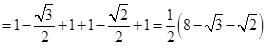
Пример 8. Найти площадь фигуры, ограниченной линиями x - 2y + 4 = 0, y = 0 и x + y – 5 = 0
Решение: Выполним построение фигуры.
Построим прямую x - 2y + 4 = 0: y = 0, x = -4, A( -4; 0); x = 0, y = 2, B(0; 2).
Построим прямую x + y – 5 = 0: y = 0, x = 5, C(5; 0); x = 0, y = 5, D(0; 5).
Найдем точку пересечения прямых, решив систему уравнений:

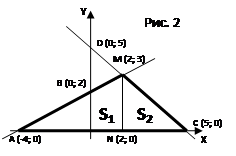 Для вычисления искомой площади разобьем треугольник AMC на два треугольника AMN и NMC, так как при изменении x от A до N площадь ограничена прямой x - 2y + 4 = 0, а при изменении x от N до С – прямой x + y – 5 = 0.
Для вычисления искомой площади разобьем треугольник AMC на два треугольника AMN и NMC, так как при изменении x от A до N площадь ограничена прямой x - 2y + 4 = 0, а при изменении x от N до С – прямой x + y – 5 = 0.
Для треугольника AMN имеем: x - 2y + 4 = 0; y = 0, 5x + 2, т. е. f(x) = 0, 5x + 2, a = -4, b = 2. Для треугольника NMC имеем: x + y – 5 = 0, y = 5 – x, т. е. f(x) = 5 – x, a = 2, b = 5.
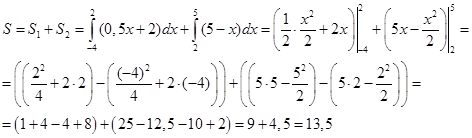
Ответ. S = 13, 5 кв. ед.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|