
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Дисциплина – Математика. Степень с рациональным показателем. Дидактический материал
Дисциплина – Математика
ФИО преподавателя Мисюк Татьяна Максимовна
электронная почта musik@inbox. ru
| Группа | Дата занятия | Тема | Срок сдачи | Форма контроля |
| ПКД-11 | 20 ноября | Тема: Степень с действительным показателем, свойства степени | 22 ноября | Решение задач |
Степень с рациональным показателем
Определение: Степенью числа 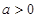 с рациональным показателем
с рациональным показателем 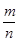 называется значение корня
называется значение корня 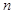 –ой степени из числа
–ой степени из числа 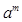 .
.
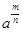 =
= 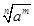 .
.
Свойства: для любых чисел 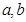 , для любых целых чисел
, для любых целых чисел 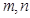
1. 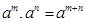 ; 2.
; 2. 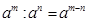 ;
;
3. 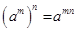 ; 4.
; 4. 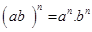 ;
;
5. 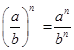 ; 6.
; 6. 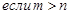 , то
, то 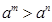 при
при 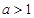 ;
; 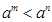 при
при 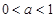 .
.
Свойства: для 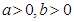 и любых рациональных чисел
и любых рациональных чисел 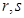
1. 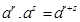 ; 2.
; 2. 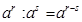 ;
;
3. 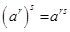 ; 4.
; 4. 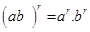 ;
;
5. 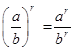 ;
;
6. 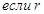 - рациональное число и
- рациональное число и 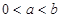 , то
, то 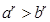 при r
при r 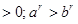 при r
при r 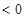
7. для рациональных чисел 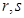 из неравенства r
из неравенства r 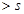 , получаем
, получаем 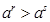 при
при 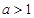 ,
, 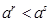 , при
, при 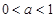 .
.
Пример 1. Представьте выражение в виде степени с рациональным показателем: а) 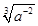 ; б)
; б) 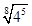 ; в)
; в) 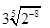 .
.
Решение:
а) 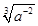 =
= 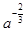
Ответ: 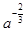
б) 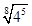 =
= 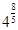
Ответ: 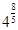
в) 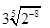 =
= 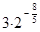
Ответ: 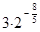
Пример 2. Представьте выражение в виде корня: а) 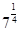 б)
б) 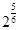 в)
в) 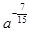
Решение:
а) 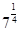 =
= 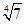
Ответ: 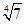
б) 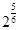 =
= 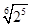 =
= 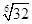
Ответ: 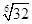
в) 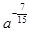 =
= 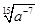
Ответ: 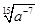
Пример 3. Найдите значение числового выражения:
а) 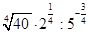 ; б)
; б) 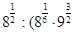 ); в)
); в) 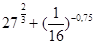 -
- 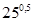
Решение:
а) 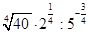 =
= 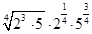 =
= 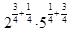 = 2 · 5 = 10. Ответ: 10
= 2 · 5 = 10. Ответ: 10
б) 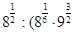 ) =
) = 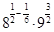 =
= 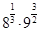 = 2 · 27 = 54 Ответ: 54
= 2 · 27 = 54 Ответ: 54
в) 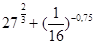 -
- 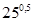 = 9 +
= 9 + 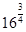 -
- 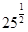 = 9 + 27 – 5 = 31 Ответ: 21
= 9 + 27 – 5 = 31 Ответ: 21
Пример 4. Упростите выражения: а) 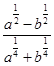 ; б)
; б) 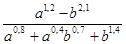 .
.
Решение:
а) 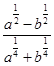 =
= 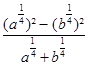 =
= 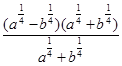 =
= 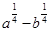 Ответ:
Ответ: 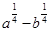
б) 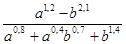 =
= 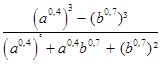 =
= 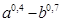 Ответ:
Ответ: 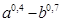
Пример 5. Сравните числа: а) 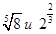 ; б)
; б) 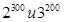
Решение: а) 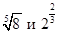 , запишем
, запишем 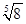 в виде степени с рациональным показателем:
в виде степени с рациональным показателем: 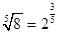 . Получаем
. Получаем 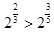 , так как
, так как 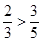 .
.
Ответ: 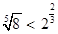 .
.
б) 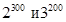 . Запишите эти числа в виде степеней с одинаковыми показателем:
. Запишите эти числа в виде степеней с одинаковыми показателем: 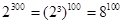 ,
, 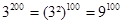 , так как 8< 9, получаем
, так как 8< 9, получаем 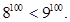
Ответ: 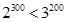 .
.
Дидактический материал
1. Представьте выражение в виде степени с рациональным показателем:
а) 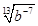 Ответ:
Ответ: 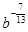 ; б)
; б) 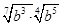 Ответ:
Ответ: 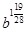 ; в)
; в) 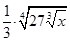 Ответ:
Ответ: 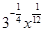
2. Представьте выражение в виде корня:
а) 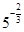 б)
б) 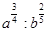 в)
в) 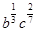 Ответ:
Ответ: 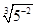 Ответ:
Ответ: 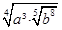 Ответ:
Ответ: 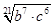
3. Найдите значение числового выражения:
а) 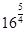 б)
б) 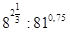 в)
в) 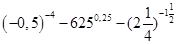 +19(-
+19(- 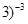
Ответ: 32 Ответ: 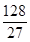 Ответ: 10
Ответ: 10
4. Упростите выражения:
а) 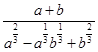 ; б)
; б) 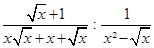 ; в)
; в) 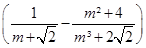 ·
· 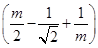 Ответ:
Ответ: 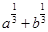 Ответ:
Ответ: 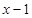 Ответ:
Ответ: 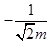
5. Сравните числа:
а) 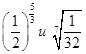 ; б)
; б) 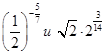 ; в)
; в) 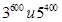 .
.
Ответ: 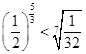 Ответ:
Ответ: 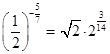 Ответ:
Ответ: 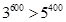 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|