Понятие функции

Определение функции можно сформулировать по-разному. Рассмотрим несколько вариантов, чтобы усвоить наверняка.

1. Функция — это взаимосвязь между величинами, то есть зависимость одной переменной величины от другой.

Знакомое обозначение y = f (x) как раз и выражает идею такой зависимости одной величины от другой. Величина у зависит от величины х по определенному закону, или правилу, которое обозначается f.

Вывод: меняя х (независимую переменную, или аргумент) — меняем значение у.

2. Функция — это определенное действие над переменной.

Значит, можно взять величину х, как-то над ней поколдовать — и получить соответствующую величину у.

В технической литературе можно встретить такие определения функции для устройств, в которых на вход подается х — на выходе получается у. Схематично это выглядит так:

В этом значении слово «функция» используют и в далеких от математики областях. Например, так говорят о функциях ноутбука, костей в организме или даже о функциях менеджера в компании. В каждом перечисленном случае речь идет именно о неких действиях.

3. Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества. Это самое популярное определение в учебниках по математике.

Например, в функции у = 2х каждому действительному числу х ставит в соответствие число в два раза большее, чем х.

Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.

Например, для функции вида

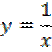
область определения выглядит так:

· х ≠ 0 (потому что на ноль делить нельзя)

И записать это можно так: D (y): х ≠ 0.

Область значений — множество у, то есть это значения, которые может принимать функция.

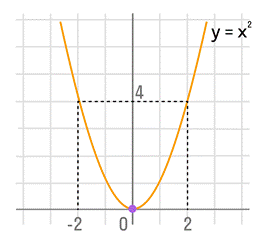
Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.

Для примера рассмотрим соответствие между двумя множествами — человек-владелец странички в инстаграм и сама страничка, у которой есть владелец. Такое соответствие можно назвать взаимно-однозначным — у человека есть страничка, и это можно проверить. И наоборот — по аккаунту в инстаграм можно проверить, кто им владеет.

В математике тоже есть такие взаимно-однозначные функции. Например, линейная функция у = 3х +2. Каждому значению х соответствует одно и только одно значение у. И наоборот — зная у, можно сразу найти х.

х	-3	-2	-1
у=3х+2	-7	-4	-1

Рассмотрим другие типы соответствий между множествами.

Например, фрукты и цвет каждого:

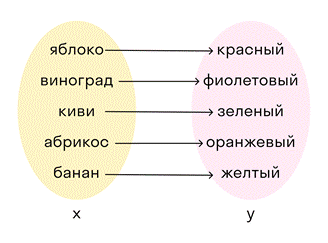
У каждого фрукта есть свой цвет. Но такое соответствие нельзя назвать взаимно-однозначным. Например, яблоко может быть и красным, и желтым и даже зеленым.

Пример такого соответствия в математике — функция у = х². Один и тот же элемент второго множества у = 4 соответствует двум разным элементам первого множества: х = 2 и х = -2.

Так на примере с фруктами можно показать соответствие, которое нельзя назвать функцией:

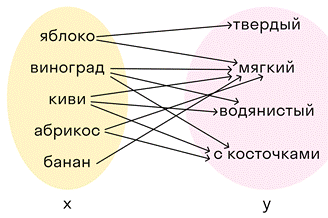
Видно, что в первом множестве есть элементы, которым соответствует два или три элемента из второго множества. Описать такое соответствие математически было бы сложнее.