11). Чему равенarcctg(-1)?. 12). При каких значениях x можно использовать выражение arcsin x?. 13). Какое уравнение не имеет корней?. 3). Что является целым числом в x = 2πn?. 5). Для какого выражения подходит область значений (− ; )?. 7). Каки

11). Чему равенarcctg(-1)?

а) 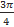б) в) − г) 0

12). При каких значениях x можно использовать выражение arcsin x?

а) − 1⩾ x⩾ 1 б) − 1⩽ x⩽ 1 в) 0> x> 1 г) − 1< x> 1

13). Какое уравнение не имеет корней?

а) sinx = 0 б) cosx = − в) sin6x = 0, 6 г) sinx =

Тригонометрические уравнения.

2 вариант

1). Какое решение имеет тригонометрическое уравнение cos(x) = a, если |a| ⩽ 1?

a) x = (-1)ⁿ arcsin(a) + π n б) x = ±arccos(a) + 2π n

в) x = arcsin(a)n + π n г) x = 2π n

2). Решите уравнение tg5x =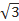

а) x = 5π n, n∈ ℤ б) x = 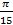+ 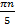, n∈ ℤ

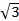в) x = - π n, n∈ ℤ г) x = -π + π n, n∈ ℤ

3). Что является целым числом в x = 2π n?

а)n б) 2 в) π г)x

4). Какой способ решения как основной можно применить для уравнения:

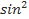x + 2sinx − 3 = 0?

а) способ разложения на множители

б) способ однородных уравнений

в) способ с применением ограниченности суммы

г) способ замены переменной

5). Для какого выражения подходит область значений (− ; )?

а) 3arctg(-x) б) arcsinx в)arctgx г) arccosx

6). Чему равенcos 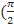+ 2π n) = …

а) 1 б) 0 в) -2 г) 7

7). Каким знаком обозначается множество целых чисел?

а) Z б) ∈ в) = г) N

8). Какое значение имеет x в уравнении cos x = 1?

а) π + 2π n, n ∈ ℤ б) − π n, n ∈ ℤ в) 2π + 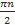, n ∈ ℤ г) 2π n, n ∈ ℤ

9). Чему равен результат выражения sin2x − 2 + cos2x после упрощения?

а) 0 б) 1 в) − 1 г) cos²x

10). Решите уравнение tgx = 0

а) x = − 2π n, n∈ ℤ б) x = π n, n∈ ℤ в) x = + π n, n∈ ℤ г) x = 2π n, n ∈ ℤ

11). Чему равенarccos(− )?

а) 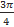б) в) − г) 0

12). При каких значениях x можно использовать выражение arccos x?

а) − 1⩾ x⩾ 1 б) )− 1< x> 1 в) 0> x> 1 г) − 1⩽ x⩽ 1

13). Какое уравнение не имеет корней?

а) sinx = 0 б) cosx = − в) sin6x = 1, 6 г) sinx =