Мгновенная скорость

Неравномерное движение может быть как прямолинейным, так и криволинейным.

Чтобы полностью описать неравномерное движение точки, надо знать её положение и скорость в каждый момент времени.

Запомни Скорость точки в данный момент времени называется мгновенной скоростью.

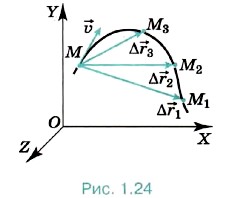Поделив вектор Δ 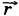₁ на промежуток времени Δ t₁ найдём такую скорость равномерного прямолинейного движения, с которой должна была бы двигаться точка, чтобы за время Δ t попасть из положения М в положение М₁. Эту скорость называют средней скоростью перемещения точки за время Δ t₁.

Обозначив её через 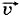_ср1, запишем: 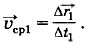Средняя скорость направлена вдоль секущей ММ₁. По той же формуле мы находим скорость точки при равномерном прямолинейном движении.

Для того чтобы определить скорость в данный момент времени, когда точка занимает положение М, найдём средние скорости за всё меньшие и меньшие промежутки времени:

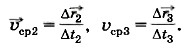
При уменьшении промежутка времени Δ t перемещения точки уменьшаются по модулю и меняются по направлению. Соответственно этому средние скорости также меняются как по модулю, так и по направлению. Но по мере приближения промежутка времени Δ t к нулю средние скорости всё меньше и меньше будут отличаться друг от друга. А это означает, что при стремлении промежутка времени Δ t к нулю отношение 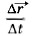стремится к определённому вектору как к своему предельному значению. В механике такую величину называют скоростью точки в данный момент времени или просто мгновенной скоростью и обозначают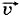

Мгновенная скорость точки есть величина, равная пределу отношения перемещения Δ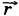

к промежутку времени Δ t, в течение которого это перемещение произошло, при стремлении промежутка Δ t к нулю.

Мгновенная скорость направлена по касательной к траектории.

Для неравномерного движения также справедлив закон сложения скоростей. В этом случае складываются мгновенные скорости.

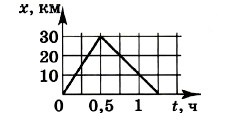A1. На рисунке представлен график зависимости координаты тела от времени. Средняя скорость движения тела равна 1) 48 км/ч 3) 40 км/ч 2) 60 км/ч 4) 0 A2. Уравнение движения тела х = 4 + 5t. Все величины выражены в СИ. Через время, равное 2 с после начала движения, скорость тела равна

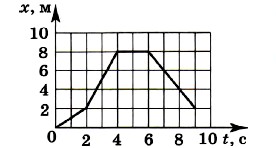
1) 7 м/с 2) 2, 5 м/с 3) 5 м/с 4) 14 м/с A3. На рисунке показана зависимость координаты тела от времени. Определите максимальное значение модуля мгновенной скорости. 1) 1 м/с 3) 2 м/с 2) 3 м/с 4) 8/9 м/с A4. Определите значения средней путевой скорости и модуля средней скорости перемещения за 9 с (см. рис. к тесту АЗ). 1) 14/9 м/с, 2/9 м/с 3) 2 м/с, 2/9 м/с 2) 2/3 м/с, 2/3 м/с 4) 1/3 м/с, 16/9 м/с

12 Следующая ⇒