
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема: Обратные тригонометрические функции: y=arcsinx, y=arccosx, y=arctgx, y=arcctgx. Свойства и графики
Урок
Тема: Обратные тригонометрические функции: y=arcsinx, y=arccosx, y=arctgx, y=arcctgx. Свойства и графики
Цели урока: ввести обратные тригонометрические функции, описать их свойства, научиться применять свойства функций для решения задач.
Задание: изучить по информационной карте тему, письменно прочитать по графикам свойства функций и выполнить упражнения.
Информационная карта к уроку
 Ход урока
Ход урока
I. Изучение нового материала:
1. Функция у=sin х на всей области определения не является монотонной, поэтому выберем отрезок 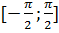 , на котором она монотонно возрастает и вспомним, что
, на котором она монотонно возрастает и вспомним, что 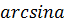 определяется как угол из отрезка
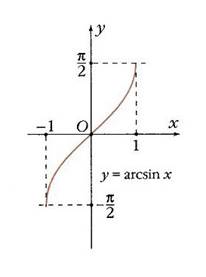
определяется как угол из отрезка 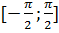 . Следовательно, можно определить обратную функцию у=arcsin х, график которой симметричен графику у=sin х на отрезке [-1; 1] относительно прямой у=х.
. Следовательно, можно определить обратную функцию у=arcsin х, график которой симметричен графику у=sin х на отрезке [-1; 1] относительно прямой у=х.
Прочитаем свойства функции.
1) D(y)=[-1; 1]
2) E(y)= 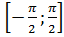
3) Функция возрастает на всей области определения.
4)  Функция нечётная, т. к. график симметричен относительно начала координат
Функция нечётная, т. к. график симметричен относительно начала координат
arcsin(-х)=- arcsin х
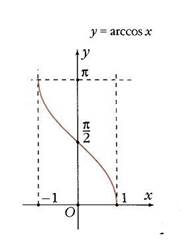
2. Аналогично определим для функции у=cos х обратную функцию на отрезке 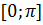 , где cos х убывает и
, где cos х убывает и 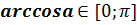 . Построим график функции y=arccosx, который симметричен графику у=cos х на отрезке [-1; 1] относительно прямой у=х.
. Построим график функции y=arccosx, который симметричен графику у=cos х на отрезке [-1; 1] относительно прямой у=х.
Прочитаем по графику свойства функции.
1) D(y)=[-1; 1]
2) E(y)= 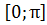
3) Функция убывает на всей области определения.
4) Функция общего вида 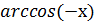 =
= 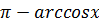
3. Т. к. функции  y=tg x
y=tg x  ; y=ctg x монотонны на области определения, то для них можно задать обратные функции:
; y=ctg x монотонны на области определения, то для них можно задать обратные функции: 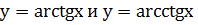
На рисунках изображены графики этих функций.
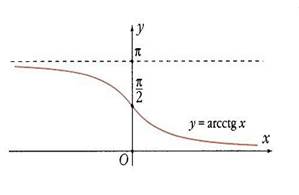
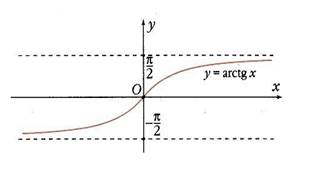 Нарисуйте эти графики и по графикам опишите свойства функций.
Нарисуйте эти графики и по графикам опишите свойства функций.
II. Выполните упражнение:
1) Найти число целых значений функции у= 12arccos х.
Решение: 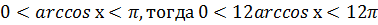
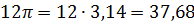 , значит, целых значений будет 37.
, значит, целых значений будет 37.
Ответ: 37
2) Найти множество значений функций: y=2arcsinx-1, y=3arccosx+2
3) Найти множество значений функции: 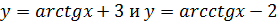
III. Дом. задание: § 43; № 750; 752
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|