
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тригонометрические подстановки
Тригонометрические подстановки
q Интегралы вида
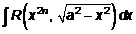 ;
; 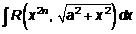 ;
; 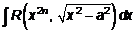
интегрируются с помощью следующих тригонометрических подстановок:
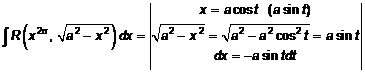 ;
;
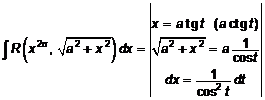 ;
;
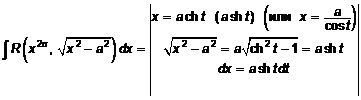 .
.
Пример 9. 19. Найти интеграл 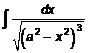 .
.
Решение:
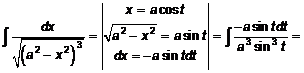
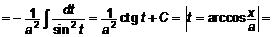
 .
.
Принимая во внимание, что 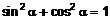 , упростим полученный ответ:
, упростим полученный ответ:
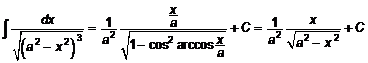 .
.
Замечание 9. 2
Для интегралов вида 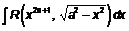 ,
, 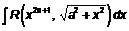 ,
, 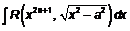 также можно использовать тригонометрические подстановки. Однако проще их вычислять, делая замену
также можно использовать тригонометрические подстановки. Однако проще их вычислять, делая замену 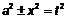 или
или 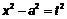 .
.
Интегрирование некоторых классов тригонометрических функций
q Интеграл вида
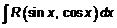 ,
,
где 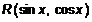 ― рациональная функция своих аргументов
― рациональная функция своих аргументов 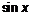 и
и 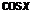 , всегда можно проинтегрировать с помощью универсальной подстановки
, всегда можно проинтегрировать с помощью универсальной подстановки 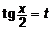 :
:
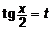
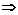
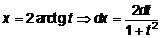 ;
;
 ;
; 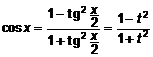 .
.
Таким образом, в результате сделанной подстановки исходный интеграл от тригонометрических функций стал интегралом от рациональной функции переменной t, то есть 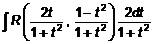 .
.
Пример 9. 20. Найти интеграл 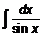 .
.
Решение:

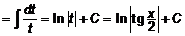 .
.
Рассмотренная подстановка дает возможность проинтегрировать любую функцию вида 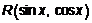 . Однако на практике она часто приводит к получению сложных интегралов от рациональных функций. Поэтому полезно знать и другие подстановки.
. Однако на практике она часто приводит к получению сложных интегралов от рациональных функций. Поэтому полезно знать и другие подстановки.
q В интеграле вида 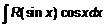 рационально сделать подстановку
рационально сделать подстановку
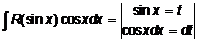 .
.
Пример 9. 21. Найти интеграл 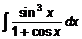 .
.
Решение:

 .
.
q Интегралы вида 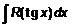 берутся с помощью подстановки
берутся с помощью подстановки
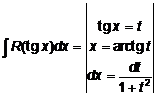 .
.
q В интегралах вида 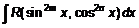 , где
, где 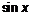 и
и 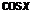 содержатся в четных степенях, делается подстановка
содержатся в четных степенях, делается подстановка
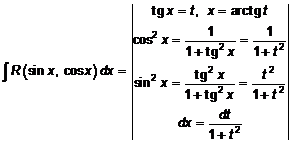 .
.
q В интегралах вида 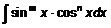 , где хотя бы один из показателей степеней нечетный, например n, а m — любое число, следует применить формулу
, где хотя бы один из показателей степеней нечетный, например n, а m — любое число, следует применить формулу 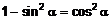 . В частности, если
. В частности, если 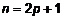 — нечетное число, то
— нечетное число, то

 .
.
q В интегралах вида 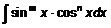 , где m и n — четные неотрицательные, используются формулы понижения степени
, где m и n — четные неотрицательные, используются формулы понижения степени
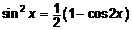 ;
; 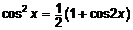 .
.
q Интегралы вида
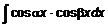 ;
; 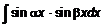 ;
; 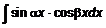 ,
,
где 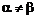 , берутся при помощи следующих формул:
, берутся при помощи следующих формул:
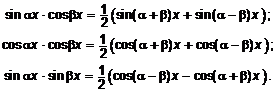
q Интегралы вида
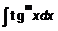 ;
; 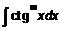 ,
,
где 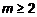 — целое число, берутся, если к подынтегральной функции прибавить и отнять
— целое число, берутся, если к подынтегральной функции прибавить и отнять 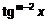 (или
(или 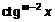 ) и применить формулу
) и применить формулу 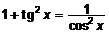 (или
(или 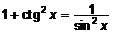 ).
).
Пример 9. 23. Найти интеграл 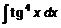 .
.
Решение:
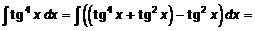
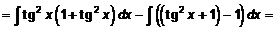
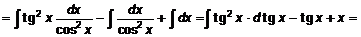
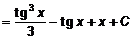 .
.
q Иногда полезно использовать тригонометрическое тождество 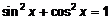 . Это удобно, если под знаком интеграла стоят выражения
. Это удобно, если под знаком интеграла стоят выражения  и
и 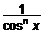 , где n — четное неотрицательное число.
, где n — четное неотрицательное число.
Пример 9. 24. Найти интеграл 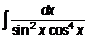 .
.
Решение:
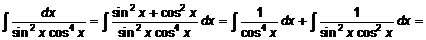
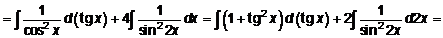
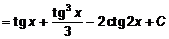 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|