Δ y=f(x0+Δx) - f(x0). (1)

Производная функции

Урок на тему: " Что такое производная? Определение производной"

Что будем изучать:
1. Введение в понятие производной.
2. Чуть-чуть истории.
3. Определение производной.
4. Производная на графике функции. Геометрический смысл производной.
5. Алгоритм нахождения производной функции.
6. Дифференцирование функции.
7. Примеры.

Введение в понятие производной

Существует множество задач совершенно разных по смыслу, но при этом есть математические модели, которые позволяют рассчитывать решения наших задач совершенно одинаковым способом. Например, если рассмотреть такие задачи как:
а) Есть некоторый счет в банке, который постоянно изменяется один раз в несколько дней, сумма постоянно растет, требуется найти с какой скоростью растет счет.
б) Завод выпускает конфеты, есть некоторый постоянный прирост выпуска конфет, найти насколько быстро увеличивается прирост конфет.
в) Скорость движения автомобиля в некоторый момент времени t, если известно положение автомобиля, и он движется по прямой линии.
г) Нам дан график функции и в некоторой точке к нему проведена касательная, требуется найти тангенс угла наклона к касательной.

Формулировка наших задач совершенно разная, и, кажется, что они решаются совершенно разными способами, но математики придумали как можно решить все эти задачи совершенно одинаковым способом. Было введено понятие производной.

В настоящее время понятие производной находит большое применение в логистике и коммерческой деятельности. Умение применять производную к исследованию функции – важный элемент математической культуры.

Чуть-чуть истории

Понятие «производная» возникло в XVII веке в связи с необходимостью решения ряда задач из физики, механики и математики.

Великий французский математик Пьер Ферма в 1629 г. Научился находить касательные к алгебраическим прямым.

В 1638г Ферма поделился этим открытием со своим земляком Рене Декартом, который тоже занимался этой проблемой и нашел свой метод построения касательных к алгебраическим кривым.

Ферма далеко продвинулся в применении дифференциальных методов. Он использовал их не только для проведения касательных, но, к примеру, для нахождения максимумов, вычисления площадей.

Однако ни Ферма, ни Декарт не сумели свести полученные научные выводы и результаты в единую систему. Тем не менее, выдвинутые идеи не пропали впустую. Многие из них легли в основу нового метода математического анализа – дифференциального исчисления.

«Дифференциальное исчисление – это описание окружающего нас мира, выполненное на математическом языке. Производная помогает нам успешно решать не только математические задачи, но и задачи практического характера в разных областях науки и техники».

Основоположниками этого метода считаются Вильгельм Лейбниц (1646 – 1716) и Исаак Ньютон (1642 – 1727).

Независимо друг от друга И. Ньютон и Г. Лейбниц разработали аппарат, которым мы и пользуемся в настоящее время. Рассматривали понятие производной в своих работах Лейбниц и Ньютон, применение нашему термину они находили в геометрии и механике соответственно.

И. Ньютон в основном опирался на физическое представление о мгновенной скорости движения, а Г. Лейбниц использовал понятие бесконечно малой.

С помощью дифференциального исчисления был решен целый ряд задач теоретической механики, физики и астрономии. В частности, ученые предсказали возвращение кометы Галлея, что было большим триумфом науки XVII века.

Очень многие великие ученые внесли свой вклад в зарождение и развитие дифференциального исчисления. Среди них – Джеймс Грегори, Якоб Бернулли, Гийом Франсуа Лопиталь, Леонард Эйлер, Карл Фридрих Гаусс. В 1797 г. термин «производная» ввел великий математик – Жозеф Луи Лагранж, перевод на русский язык получается из французского слова derivee, он же и ввел современные обозначения производной которые мы рассмотрим позже.

Чуть позже мы с вами узнаем, что производная определяется через предел, но существует небольшой парадокс в истории математики. Математики научились считать производную раньше, чем ввели понятие предела и собственно поняли, что же такое производная.
Обратите внимание, что наш учебник называется «Алгебра и начала математического анализа». Мы начинаем изучать новый раздел математики «Математический анализ». В нашей учебной программе мы будем изучать только основы – «начала» анализа. Одна из тем этого раздела – «Понятие производной». Математика в школе – это достаточно сложный предмет и самое главное для учащихся – понять, зачем она нужна. Мы изучаем производную. А так ли это важно в жизни? Давайте попробуем вместе в этом разобраться.

Продолжить урокхочется словами Бориса Пастернака

Во всем мне хочется дойти

До самой сути.

В работе, в поисках пути,

В сердечной смуте.

До сущности протекших дней,

До их причины,

До оснований, до корней,

До сердцевины.

И сейчас мы постараемся дойти до самой сути определения производной и покажем ее применение в различных областях знаний.

Сегодня у нас будет встречаться много новых терминов. «Производная» – это то, что «произведено» какой-то функцией. Простой пример: Яйцо – это производная курицы. Понятие производной довольно трудное, т. к. основано на абстрактном восприятии. Мы рассмотрим ситуацию, известную нам из повседневной жизни.

Мы едем из Кирова до Орлова (78 км). Рассмотрим график этого движения. На оси абсцисс – время t, по оси ординат – пройденный путь s(t). На весь путь ушло 1, 5 часа. Как узнать, с какой скоростью мы ехали. (Пройденный путь разделить на время 78: 1, 5 = 52(км/ч)

- Мы всё время ехали с такой скоростью? (Нет, в течение пути она менялась, могла быть и больше 52 и меньше).

- Так какую скорость мы получим? (Среднюю).

- Рассмотрим участок времени Δ t (пусть с 10. 30 до 11 часов). За это время мы проехали отрезок пути Δ s (пусть 40 км). С какой скоростью мы проехали этот отрезок пути? (40: 1 = 40 км/ч или Δ s: Δ t).

- Какая скорость получится? (Средняя) Vср. = Δ s: Δ t

- Если мы уменьшим отрезок времени до 0, что произойдет со скоростью? Представьте себе, на посту ГИБДД скорость отслеживается с помощью радара. В момент пересечения луча радара автомобилем на табло радара высвечивается цифры скорости. Будет ли она равна средней скорости (может да, а может, нет). Как можно назвать такую скорость (мгновенной), т. к. мы рассматриваем скорость в какое-то мгновение.

Если отрезок времени стремится к 0, скорость из средней превращается в мгновенную:

Вот мы подошли к понятию производной пути. Производная обозначаетсяy', f''(x).

Производная пути – это мгновенная скорость. Vмгнов. = S´ (t)

- Где мы можем увидеть значение мгновенной скорости? (Радар, спидометр).
- Можем мы увидеть значение средней скорости? (Нет, её можно вычислить)

Перейдем от конкретной ситуации к любой математической функции f(x) по той же схеме.

Определение производной

Изучая поведение функции y=f(x) около конкретной точки x₀, важно знать, как меняется значение функции при изменении значения аргумента. Для этого используют понятия приращений аргумента и функции.

Пусть функция y=f(x) определена в точках x₀ и x₁. Разность x₁− x₀ называют приращением аргумента (при переходе от точки x₀ к точке x₁), а разность f(x₁) - f(x₀) называют приращением функции.

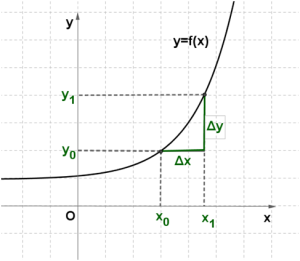
Приращение аргумента обозначают Δ x (читают: дельта икс; Δ — прописная буква греческого алфавита " дельта"; соответствующая строчная буква пишется так: δ ). Приращение функции обозначают Δ y или Δ f.

Итак, x₁-x₀=Δ x, значит, x₁=x₀+Δ x.

f(x₁) - f(x₀) = Δ y, значит,

Δ y=f(x0+Δ x) - f(x0). (1)

Нельзя истолковывать термин " приращение" как " прирост".

Пусть функция y=f(x) определена на некотором интервале, содержащим внутри себя некоторую точку xₒ. Приращение аргумента Δ x – не выходит из нашего интервала. Найдем приращение Δ y и составим отношение Δ y/Δ x, если существует предел этого отношения при Δ x стремящимся к нулю, то указанный предел называют производной функции y=f(x) в точке xₒ и обозначают f’(xₒ ).

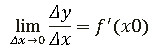
Попробуем объяснить, что такое производная не математическим языком:
На математическом языке: производная - предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю.
На обычном языке: производная – скорость изменения функции в точке xₒ.
Давайте посмотрим на графики трех функций:

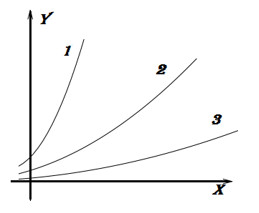
Ребята, как вы думаете, какая из кривых растет быстрее?
Ответ, кажется, очевиден всем 1 кривая растет быстрее остальных. Мы смотрим, насколько круто идет вверх график функции. Другими словами — насколько быстро меняется ордината при изменении х. Одна и та же функция в разных точках может иметь разное значение производной — то есть может меняться быстрее или медленнее.

Производная на графике функции. Геометрический смысл производной

Теперь давайте посмотрим, как же найти производную с помощью графиков функции:

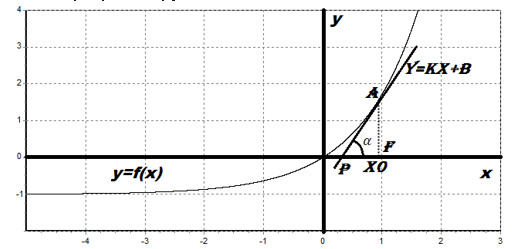
Посмотрим на наш график функции: Проведём в точке c абсциссой xₒ касательную к графику функции. Касательная и график нашей функции соприкасаются в точке А. Нам надо оценить, насколько круто вверх идет график функции. Удобная величина для этого — тангенс угла наклона касательной.

Определение. Производная функции в точке xₒ равна тангенсу угла наклона касательной, проведённой к графику функции в этой точке.

f' (xₒ )=tg(α )

Угол наклона касательной выбирается как угол между касательной и положительным направлением оси абсцисс.
И так производная нашей функции равна:

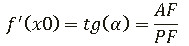
И так, производная в точке xₒ равна тангенсу угла наклона касательной, это геометрический смысл производной.

Алгоритм нахождения производной функции

Алгоритм нахождения производной функции y=f(x).
а) Зафиксировать значение x, найти f(x).
б) Найти приращение аргумента x+ Δ x, и значение приращения функции f(x+ Δ x).
в) Найти приращение функции Δ y= f(x+ Δ x)-f(x).
г) Составить соотношение: Δ y/Δ x
д) Вычислить

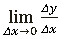
- это и есть производная нашей функции.

Дифференцирование функции

Если функции y=f(x)имеет производную в точке x, то ее называют дифференцируемой в точке x. Процесс нахождения производной называют дифференцированием функции y=f(x).
Вернемся к вопросу непрерывности функции. Если функция дифференцируема в некоторой точке, тогда к графику функции в этой точке можно провести касательную, функция не может иметь разрыв в этой точки, тогда просто напросто нельзя провести касательную.
И так запишем выше сказанное как определение:
Определение. Если функция дифференцируема в точке x, то она непрерывна в этой точке.
Однако, если функция непрерывна в точке, то это не значит, что она дифференцируема в этой точке. Например, функция y=|x| в точке x=0 непрерывна, но касательную провести нельзя, а значит и производной не существует.

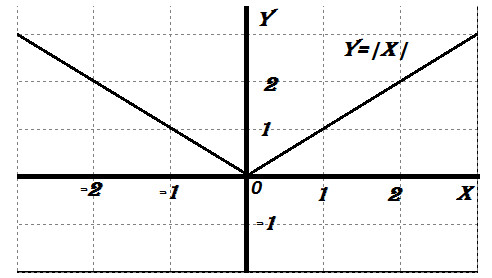
Примеры производной

Найти производную функции: y=3x
Решение:
Будем пользоваться алгоритмом поиска производной.
1) Для фиксированного значения x, значение функции y=3x
2) В точке x+ Δ x, y=f(x+ Δ x)=3(x+ Δ x)=3x+3 Δ x

3) Найдем приращение функции: Δ y= f(x+ Δ x)-f(x)= 3x+3 Δ x-3x=3Δ x

4) Составим соотношение:

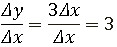
5)Найдем предел:

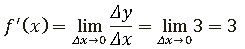
Ответ: f' (x)=3

Найти производную функции y=5x²

Решение:
Будем пользоваться алгоритмом поиска производной.

1)Для фиксированного значения x, значение функции y=5x²

2)В точке x+ Δ x, y=f(x+ Δ x)=5(x+ Δ x)^²=5(x²+2xΔ x+Δ x²)

3)Найдем приращение функции:

Δ y= f(x+ Δ x)-f(x)= 5x²+10xΔ x+5Δ x²-5x²=10xΔ x+5Δ x²

4) Составим соотношение:

5)Найдем предел:

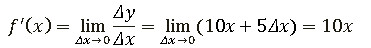
Ответ: f' (x)=10x

Найти производную функции y=2x²-x+1

Решение:

Будем пользоваться алгоритмом поиска производной.

1)Для фиксированного значения x, значение функции

y=2x²-x+1

2)В точке x+ Δ x, y=f(x+ Δ x)=2(x+ Δ x)²-(x+ Δ x)+1= =2(x²+2xΔ x+Δ x² )-(x+ Δ x)+1

Найдем приращение функции: Δ y= f(x+ Δ x)-f(x)= = 2x²+4xΔ x+ 5Δ x²-(x+ Δ x)+1-2x²+x-1= =4xΔ x+5Δ x²-Δ x
3) Составим соотношение:

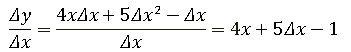
5)Найдем предел:

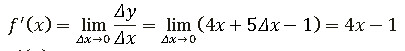
Ответ: f' (x)=4x-1

Операция вычисления производной называется дифференцированием.

- Где в жизни применяется понятие производной? В физике – это скорость, ускорение, работа; в математике – это исследование различных функций при практических расчетах в автомобилестроении, судостроении, электронике и т. д.

Задачи для самостоятельного решения

Найти производную функции по алгоритму:
а) y=5y=5;
б) y=10xy=10x;
в) y=2x2+xy=2x2+x;
г) y=3x3y=3x3.