
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Понятие перпендикулярных плоскостей
Понятие перпендикулярных плоскостей
Две плоскости, которые пересекаются, называются перпендикулярными, если третья плоскость, проведенная перпендикулярно к линии пересечения этих плоскостей, пересекает их по перпендикулярным прямым. На рис. 216 α  β, так как плоскости α и β пересекаются по прямой с, плоскость γ, перпендикулярная к с, пересекает α и β по прямым а и b, перпендикулярные.
β, так как плоскости α и β пересекаются по прямой с, плоскость γ, перпендикулярная к с, пересекает α и β по прямым а и b, перпендикулярные.

Определение перпендикулярности плоскостей не зависит от выбора плоскости γ. Действительно, возьмем другую плоскость γ 1, перпендикулярную к прямой с (рис. 217).
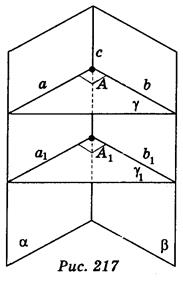
Поскольку с  γ и прямые a и b лежат в плоскости β и пересекаются в точке А, то с
γ и прямые a и b лежат в плоскости β и пересекаются в точке А, то с  а, с
а, с  b (по определению перпендикулярности прямой и плоскости).
b (по определению перпендикулярности прямой и плоскости).
Аналогично с  а1, с
а1, с  b1. Кроме того, а и а1b, b и b1 лежат соответственно в плоскостях α и β. Следовательно, а || а1 и b || b1. Так а
b1. Кроме того, а и а1b, b и b1 лежат соответственно в плоскостях α и β. Следовательно, а || а1 и b || b1. Так а  b, а || a1 и b || b1, то а1
b, а || a1 и b || b1, то а1  b1
b1
Решение задач
1. Приведите примеры моделей перпендикулярных плоскостей из окружения.
2. Покажите на модели прямоугольного параллелепипеда перпендикулярны грани (плоскости).
3. Дано изображение куба ABCDA1B1C1D1. Укажите плоскости, которые перпендикулярны к плоскости:
а) АВС; б) ADC1; в) АСС1.
4. На двух перпендикулярных плоскостях выбрали по прямой. Может ли случиться, что эти прямые:
а) параллельны; б) пересекаются; в) скрещивающиеся?
Ответ проиллюстрируйте примерами из окружения.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|