Продолжение темы 6

Рассмотрим варианты намотки:

1. Продольно-поперечная намотка: n=2, j₁=0⁰, j₂=p/2, тогда 2h₁-h₂=0 или h₂/h₁=2.

2. Спиральная намотка: число слоев n=1, угол намотки j₁=j₀, тогда

h(3соs²j₀-1)=0, cos²j₀=1/3 и j₀=54⁰44^¢, что было получено раньше.

3. Спиральная намотка с кольцевым усилением: n=2, j₁=j, j₂=p/2, тогда h₂/h₁=3cos²j-1, и эта структура может существовать, когда отношение h₂/h₁³ 0, то есть когда угол j£ j₀.

4. Спиральный слой с осевым усилением: n=2, j₁=j, j₂=0 и h₂/h₁=1/2(1-cos²j).

Тогда при j< j₀ спиральный слой должен быть усилен кольцевыми нитями, а при j> j₀ - продольными. Оптимальные соотношения толщин h₂/h₁, при изменении угла j приведены на рис 2. 4.

Теперь рассмотрим общий случай нагружения, когда все три усилия плоской задачи не равны нулю. В случае оптимальной структуры связь между деформациями имеет вид e_a=e_b=e₁_i=e₂_i=e, e_a_b=e₁₂ⁱ и соотношения упругости (2. 18) примут вид

N_a=(B₁₁+B₁₂)e; N_b=(B₁₂+B₂₂)e; N_a_b=(B₃₁+B₃₂)e. (2. 25)

Исключая деформацию e из соотношений (2. 25), получим два условия для получения расположения армирующих элементов по траектории главных напряжений

(В₁₁+В₁₂)N_b-(B₂₁+B₂₂)N_a и (B₃₁+B₃₁)(N_a+N_b)-(B₁₁+2B₁₂+B₂₂)N_a_b=0. (2. 26)

Тогда, используя физические соотношения для каждого слоя с учетом соотношения между деформациями и выражением e в форме (2. 23), напряжения в слоях материала можно представить в виде

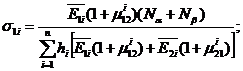
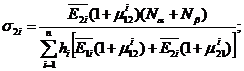
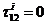. (2. 27) Для равнопрочной структуры из (2. 27) можем получить уже известное условие (2. 12) 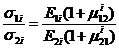. Если материал во всех слоях одинаков, то после подстановки коэффициентов В_pq, выражения (2. 26) примут вид

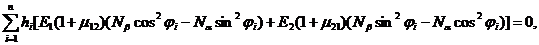(2. 28)

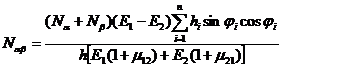(2. 29)

Условие (2. 28) определяет оптимальную схему армирования не единственным образом в соответствии с распределением нормальных усилий N_a и N_b, которые должны иметь одинаковый знак. Касательное усилие N_a_b при этом не может быть задано произвольно и должно удовлетворять условию (2. 29). Условие N_a_b=0 (N_a¹ 0, N_b¹ 0) определяет симметричную схему армирования j₁=j, j₂=-j. Максимально допустимое значение N_a_b, как это следует из (2. 28), реализуется при j=±45⁰ и равно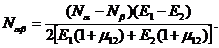

На примере проиллюстрируем определение оптимальной структуры без учета связующего для цилиндрической оболочки радиусом R, нагруженной внутренним давлением p и крутящим моментом М. Выражения для усилий определяются зависимостью

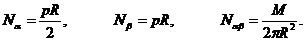
Выражения (2. 28), (2. 29), если считать Е₂=m₁₂=m₂₁=0, примут вид:

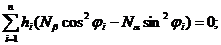
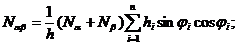
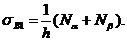
Тогда толщина оболочки равна 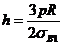и оптимальные схемы армирования будут отвечать условиям

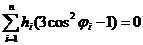и 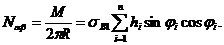(2. 30)

Если оболочка изготовлена одним семейством спиральной намотки под углом j₀, то равенства (2. 30) дадут условие j₀=54⁰44^¢ и ограничение по крутящему моменту М= 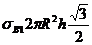(структура при j₀=±54⁰44¢ воспринимает только давление). Если ввести кольцевую подмотку с толщиной h₂ и углом j₂=p/2, то из равенства (2. 30) получим условия на толщины кольцевого h₂ и спирального h₁ слоев в виде 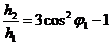и ограничение на крутящий момент М=s_в12pR²h₁sinj₁cosj₁. То есть кольцевой слой не участвует в работе на кручение оболочки, но разгружая спиральный слой, позволяет увеличить диапазон изменения крутящего момента. С учетом того, что 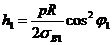, максимальный крутящий момент М_max=ppR³tgj₁.

Тема 7 3. ПРОЕКТИРОВАНИЕ ТОНКОСТЕННЫХ СТЕРЖНЕЙ (2 ч. )

Тонкостенные стержни широко используются в ракетно-космической технике. Это многочисленные тяги к рулям управления летательных аппаратов, стержни крепления двигателей и отдельных отсеков между собой. В основном эти стержни работают на растяжение-сжатие. Наиболее ответственный момент работы таких стержней связан с действием сжимающих нагрузок. Рассмотрим порядок проектирования таких стержней.

Применяемые в конструкции стержни чаще всего бывают трубчатого сечения. Параметры такого стержня приведены на рис. 3. 1. Примем, что искомыми параметрами являются радиус стержня R, толщина – h и угол укладки волокон ±j. Известными будут его длина l и сжимающая сила Р. Структуру стенки стержня, будем считать, образованной двухслойной намоткой: ±j и p/2. Угол p/2 необходим для структуры, исходя из конструктивно – технологических соображений, так как это обеспечивает работу при возможных изменениях нагрузки, растрескивании связующего, повышении местной устойчивости и позволяют присоединять концевые узлы крепления.

Целевая функция при известной длине стержня представляет массу поперечного сечения и может быть записана в виде М=2pRhr. Здесь r - плотность материала, h - суммарная толщина и равна h=h_j+h_К, h_j - спиральный слой, h_к - кольцевой слой. В выражении для массы не учитывается длина и масса металлической законцовки стержня. В целевую функцию входит толщина стенки стержня, которая косвенно учитывает угол укладки j.

Запишем ограничения, которым должна удовлетворять конструкция при удовлетворении условия М=min.

1. Ограничение по прочности. Если это условие должно удовлетворяться для волокна и связующего, то представим его в форме:

- для волокна 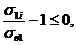(3. 1)

- для связующего 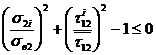. (3. 2)

Для этого в каждом слое необходимо вычислить эти напряжения, в которые войдут относительные толщины слоев. Относительная толщина кольцевой подмотки обычно задается из технологических соображений, поэтому считается заданной, а искомой будет полная толщина стенки и сам угол намотки спирального слоя j. Величины s₁_i, s₂_i, t₁₂ⁱ находится по известной схеме расчета от действия сжимающего усилия N_x=P/2pR (N_y=0, N_xy=0). Из физических соотношений 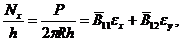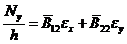находим деформации стенки e_x и e_y, а затем деформации e₁_i и e₂_i вдоль и поперек армирования слоев стержня по формулам

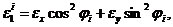
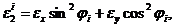
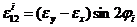И наконец напряжения в этих слоях

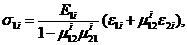
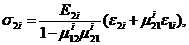
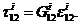
2. Условие потери устойчивости стержня по Эйлеру.

Считаем, что концы стержня шарнирно оперты и формула записывается в виде 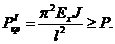Здесь для трубчатого стержня круглого сечения момент инерции J=pR³h, а средний модуль упругости структуры Е_x вычисляется по обычным формулам и равен Е_x= 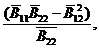где коэффициенты 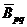ортотропной структуры, в которые входят известные относительные толщины слоев 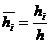, вычисляются известным способом. Неизвестной остается общая толщина стенки стержня h. Тогда формулу Эйлера можно представить в форме

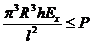. (3. 3)

3. Условие местной потери устойчивости стенки, как цилиндрической оболочки. Приближенную формулу для ортотропной структуры стенки оболочки можно представить в виде

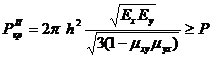
Это ограничение не зависит от радиуса и его можно разрешить относительно толщины h, которая будет минимально допустимой

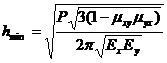(3. 4)

4. Ограничение по частоте колебания стержня. Это ограничение является обязательным и имеет вид 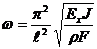> w_зад, где r - плотность материала, w_зад- заданное значение частоты. Или с учетом выражений J=pR³h, F=2pRh приведем формулу к виду

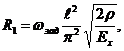(3. 5)

где R₁- минимальное значение радиуса, при котором может быть обеспечено это условие.

Эти четыре ограничения можно реализовать графически, построив функции по параметрам R=R(h) при заданном угле j. Для каждого угла j можно определить область существования оптимальных параметров h и R, и найти минимальную площадь сечения. Рассмотрим пример определения оптимальных параметров сечения стержня. Примем для стержня следующие значения характеристик материала: E_x=18750 МПа, Е_y= 43750 МПа, j=45⁰, r=1, 55г/см³. Тогда ограничения (3. 4) и (3. 5) дают минимальные значения толщины h_min=0, 31мм, и радиуса R_min=41, 2 мм. Все расчеты по принятым ограничениям приведены на графиках рис. 3. 2.

В рассмотренном примере, как видно из графика, оптимальные параметры определяются единственными значениями h и R на пересечении линий 3 и 4, так как в этом случае удовлетворяются и два других ограничения.

Тема 8 4. ОПТИМАЛЬНОЕ АРМИРОВАНИЕ ПЛАСТИН (4 ч. )

Пример 1 [4]: Рассмотрим изгиб прямоугольной шарнирно-опёртой квадратной пластины со стороной “a” (рис. 4. 1). Поверхность пластины нагружена равномерно распределенной нагрузкой q. Рассмотрим известное решение Навье в тригонометрических рядах для этой задачи, удерживая только первый член прогиба 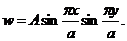Для ортотропной пластины имеем известное решение в виде:

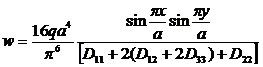. (4. 1)

Максимальное значение прогиба находится в точке пластины при x=y=a/2 и равно 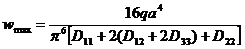. Предположим, что пластина армирована равнопрочной тканью, для которой Е₁=Е₂=Е, G₁₂=G, m₁₂=m₂₁=m. Располагая волокна вдоль координатных осей, получим следующие значения цилиндрических жесткостей:

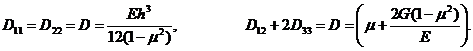
В этом случае максимальное значение прогиба равно

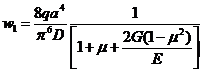
Теперь найдем оптимальное направление траекторий укладки волокон, при которой жесткость пластин будет максимальной. Для этого воспользуемся ранее рассмотренным подходом при определении оптимального армирования в точке. Используя полученное решение, определим напряжение в пластине с помощью физических соотношений

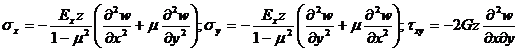куда необходимо подставить решение (4. 1) и полученные выражения в условие 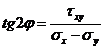откуда и находится оптимальный угол армирования. В нашем случае для квадратной пластины s_x=s_y. Поэтому tg2j=¥ или 2j=p/2. Тогда угол армирования равен j= ± p/4, то есть волокна необходимо направлять по диагоналям. Проверим полученное решение. Для равнопрочной ткани вычислим модули жесткости в направлении осей x и y при угле укладки j= ±45⁰ по формуле

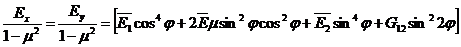что дает соотношение 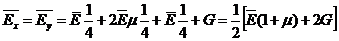. Принимая для ткани известное выражение для изотропного материала 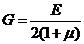, полученную выше формулу можно переписать в виде: 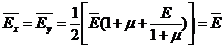. Тогда максимальный прогиб в центре пластины с учетом того, что [D₁₁+2(D₁₂+2D₃₃)+D₂₂]=4D, равен .

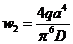Оценим эффективность этих двух структур для одинаковых по геометрии пластин. Вычислим отношение максимальных прогибов

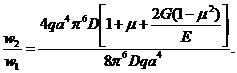
Для стеклоткани, приняв m=0, 15 и G/E=0, 1, найдем w₂/w₁=0, 5+0, 065+0, 0983=0, 663. Для ткани из углепластика, приняв m=0, 13 и G/E=0, 05, получим w₂/w₁=0, 5+0, 075+0, 09775=0, 673, то есть жесткость пластинки, армированной по траекториям главных напряжений, существенно выше.

Пример 2: Рассмотрим прямоугольную панель, армированную под углами ±j, размерами а´ b и нагруженную сжимающими усилиями N вдоль оси x (рис. 4. 2). В данной задаче, при заданных размерах пластины и нагрузке, искомыми параметрами будут толщина h и угол укладки ±j. Естественно такая структура при разрушении связующего становится механизмом, но в данной задаче найдем оптимальный угол укладки с позиции работы пластины на устойчивость, прочности материала и минимальной массы. Целевая функция - масса конструкции представляется в виде М=a^.b^.r× h. Функция массы линейно зависит от толщины пластины. Запишем ограничения, которым должна удовлетворять панель. Так как пластина имеет только два угла направления волокон, то она способна воспринимать нагрузку пока не разрушилось связующее. Иначе такая структура становится механизмом и необходимо добавление третьего слоя с иным направлением волокон, чем ±j. Тогда ограничение по прочности с учетом работы связующего запишем в форме

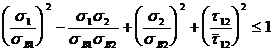Это выражение для однонаправленных материалов можно представить для каждого слоя отдельно по прочности в направлении волокон 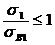и по прочности связующего от действия напряжений s₂ и t₁₂ в виде: 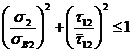и выбрать из этих условий необходимую толщину.

Второе ограничение должно обеспечивать общую потерю устойчивости пластины при шарнирном опирании по всем сторонам. Условие запишем с учетом соотношений сторон с=а/b и числе полуволн n=1 в направлении оси y.

Тогда ограничение принимает вид [8]

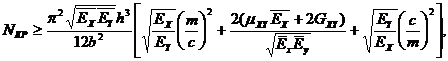
где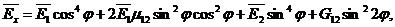

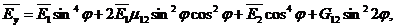
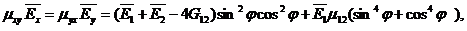
m - число полуволн, образующиеся при потере устойчивости в направлении оси x. Минимальное значение критической нагрузки зависит от числа полуволн. Число m определяется свойствами материала пластины и его можно установить по геометрическим и жесткостным параметрам, то есть

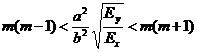Теперь необходимо выбрать алгоритм решения задачи оптимизации. Это может быть метод случайного поиска с многократным решением прямой задачи. В этом случае беря ряд произвольных точек в пространстве проектирования (то есть, задаваясь углами укладки волокон и толщинами слоя), вычисляем целевую функцию и ограничения, после чего выбираем новые значения параметров, при которых выполняется направление к минимальному весу конструкции. Для рассматриваемой пластины этот подход можно проиллюстрировать графически.

Рассмотрим пример. Пусть материалом конструкции является стеклопластик со следующими свойствами однонаправленной ленты:

модуль упругости вдоль и поперек направления волокон равны: Е₁=60 ГПа, Е₂=10 ГПа, модуль сдвига G₁₂=4 ГПа, коэффициент Пуассона m₁₂=0, 25, прочность материала вдоль направления волокон s_в1=1200 МПа, поперек направления волокон при растяжении s⁺_в2=20 МПа, при сжатии s ^- _в2=-100 МПа, прочность при сдвиге t₁₂=30 МПа. Сжимающую нагрузку принимаем N=100кПа× м. Рассмотрим, как меняются напряжения s₁, s₂, t₁₂ в слоях и толщина пластины h при изменении угла направления волокон j в диапазоне 0£ j£ p/2 (рис. 4. 3).

Использование ограничения по устойчивости позволяет при постоянном значении сжимающей силы построить кривые зависимости изменения толщины пластины от изменения угла укладки и изменение за счет этого соотношения жесткости в направлении осей x и y. Эти зависимости приведены на рис. 4. 4. Там же приведены необходимые толщины при удовлетворении условия прочности. Как видно из построенных зависимостей, определяющим условием является ограничение по устойчивости пластины во всем диапазоне изменения углов укладки волокон. На графике нанесены значения толщины при m=1 и m=2 для заданного отношения сторон - кривые 1 и 2 соответственно. Эти значения совпадают при j=45⁰. Там же приведен случай для квадратной пластины (кривая 3). Для заданной пластины толщину конструкции определяет нижняя граница значений толщины при m=1 и m=2 и оптимальная величина ее будет h=5, 6мм в диапазоне угла укладки волокон j»60⁰. Линия 4 характеризует изменение толщин по углу укладки при ограничении по прочности.

Тема 9 5. ОПТИМАЛЬНОЕ АРМИРОВАНИЕ БАЛОЧНЫХ КОНСТРУКЦИЙ (лопасть вертолета) (6 ч. )

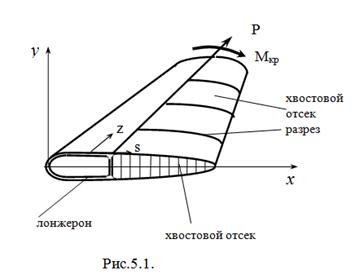
Рассмотрим лопасть вертолёта, которая является классическим примером длинномерной балки. На рис. 5. 1 показана схема лопасти, нагрузки и направления осей. Лопасть, по форме и характеру работы, представляет собой подвижное крыло, которое набегает на воздушный поток, при этом скорость обтекания переменна по длине. За счет обтекания лопасти потоком создаются аэродинамические силы, которые можно свести к перерезывающей силе Q_y, крутящему M_z и изгибающему M_x моментам. Эти силовые факторы определяют напряжения и перемещения лопасти при передвижениях по аэродрому. Основная расчетная нагрузка на лопасть образует центробежная сила P при вращении лопасти на рабочих режимах полета и крутящий момент М_z.

Геометрия лопасти известна. Конструкция, не считая узла крепления, состоит из лонжерона, расположенного в передней части сечения (рис. 5. 1) и хвостового отсека с поперечными разрезами. Этот отсек необходим для образования подъемной силы, а всю нагрузку воспринимает лонжерон. Таким образом, вес хвостовой части известен и проектированию подлежит лонжерон. Основным расчетным случаем является полетный случай с максимальной скоростью вращения лопастей. Остальные случаи полета, посадки, маневрирования по аэродрому и стоянки являются поверочными.

Основными ограничениями, накладываемыми на конструкцию при проектировании, будут прочность от растягивающих центробежных сил и крутильная жесткость лопасти или предельный угол закручивания концевого сечения q_пр. Теперь рассмотрим структуру материала лонжерона. Для восприятия переменных по длине нормальных и крутящих нагрузок, как известно, необходимо иметь три слоя с разным направлением волокон. Оптимальными направлениями будут для первого слоя (толщиной h₁), угол укладки j₁=0 и двух других слоев (толщиной h₂) углы укладки j₂=-j₃=p/4. Таким образом, пространство проектирования определяется двумя параметрами h₁ и h₂ и целевая функция, масса лонжерона, имеет вид М=LS(h₁+h₂)r, где L - длина лонжерона, S - длина периметра сечения лонжерона, r - плотность материала.

Запишем ограничения, которые необходимо удовлетворить при определении толщин.

1. Ограничение по прочности в каждом слое, которое позволяет найти необходимые толщины, удовлетворяющие этому ограничению:

- прочность вдоль волокна 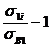£ 0

- прочность связующего 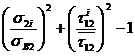£ 0

2. Ограничение по жесткости при кручении. Погонный угол закручивания сечения 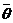определяется с помощью теоремы Кастильяно и для сечения расчетная формула имеет вид:

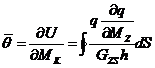. (5. 1)

Здесь 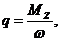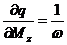, где w - удвоенная площадь поперечного сечения лонжерона, ограниченная наружным контуром. Погонный угол закручивания в сечении q не должен превышать допускаемое значение q_доп. Для композитного лонжерона сдвиговая жесткость G_zsh=B₃₃. В расчетном сечении имеем известное значение момента М_z, поэтому формулу (5. 1) можем записать в виде

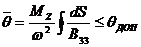3. Технологические ограничения. Так как толщина элементарного слоя композита d_эл известна, то толщина слоев h₁ и h₂ должна быть кратной элементарной толщине, то есть h₁=n₁d_эл_,h₂=n₂d_эл, где n₁ и n₂ – количество элементарных слоев в слоях 1 и 2. Количество слоев n₂ должно быть четным числом, так как этот слой имеет два направления укладки волокон.

4. Ограничения по собственным частотам колебаний. Для лопасти вертолета такое ограничение является достаточно сложным из-за того, что скорость набегающего потока по длине лопасти переменна и таких резонансных частот будет достаточно много в диапазоне эксплуатации вертолета. Гораздо проще такое ограничение будет реализовываться для лопастей ветряков, так как для них оно имеет одно верхнее значение w_max. В этом случае ограничение примет вид

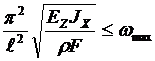Для определения напряженно-деформированного состояния в лонжероне необходимо выбрать расчетную схему. Для длинномерной конструкции лонжерона такой схемой является балочная теория, в которой принято считать контур недеформированным, а изменения деформаций в поперечном сечении соответствуют закону плоскости. В рабочем состоянии лопасть становится прямой и каждое сечение подвергается растяжению и кручению. Тогда для однозамкнутого сечения лонжерона деформации определяются с помощью физических соотношений, которые имеют вид:

- для продольных деформаций ,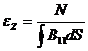

- для сдвиговых деформаций ,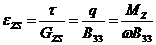

где .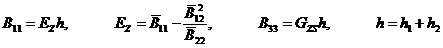

Тогда можно определить деформации в слоях с помощью формул преобразования:

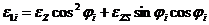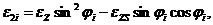
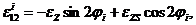
а затем и напряжения, используя физические соотношения

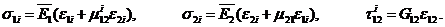
Теперь, когда сформулированы целевая функция и ограничения, можно определить минимум целевой функции, которая напрямую зависит от толщины стенок лонжерона. Толщина стенок переменна по длине лонжерона, так как по длине меняются нагрузки и может меняться площадь поперечного сечения. Так как целевая функция зависит от двух параметров, то легко проделать графическое построение изменения этих толщин и определить в зоне удовлетворения всех ограничений минимальные значения параметров.

Рассмотрим пример проектирования лонжерона, выполненного из стеклопластика. Расчет проведем без учета связующего. Пусть геометрические параметры лонжерона и свойства материала равны L=10, 6 м, S=0, 25 м,

w=2´ 10^-2 м², Е₁=65000 МПа, σ _в1=1200 МПа, δ _эл=0, 6 мм.

Структура лонжерона состоит из продольного слоя (h₁, j₁=0) и спирального слоя (h₂, j₂=±p/4). В расчетном сечении действуют нагрузки: Р=450 кН, M_Z=500 Нм. Максимально допустимый угол закручивания концевого сечения q_max £ 5⁰. Результаты расчета представлены в виде графиков на рис. 5. 2. Здесь Ι - ограничение по прочности продольного слоя 1; Ι Ι - ограничение по прочности спирального слоя; III - ограничение по жесткости; 1 - расчетная оптимальная точка; 2 - оптимальная точка с учетом технологической толщины монослоя.

В точке 1 расчетные толщины h₁ и h₂ удовлетворяют всем рассмотренным ограничениям (кроме ограничения по частоте), но с учетом технологической толщины монослоя (d_эл=0, 6 мм) реальная толщина слоев в сечении будет h₁=1, 2 мм, h₂=3 мм, а суммарная толщина стенки h=4, 2 мм. Если принять толщину продольного слоя h₁=0, то в этом случае h₂=7, 2 мм, что существенно больше, чем двухслойная структура.