
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
1. Основы комбинаторики.
Тема: Приёмы решения комбинаторных и вероятностно-статистических задач
План:
1. Основы комбинаторики.
1. 1 Понятие о комбинаторике. Перебор вариантов. Правила умножения и сложения.
1. 2 Размещения, перестановки и сочетания с повторением и без повторения.
1. 3 Основной закон комбинаторики
2. Элементы теории вероятностей.
2. 1 Пространство элементарных событий. Событие. Достоверное и невозможное события
2. 2 Классическое определение вероятности. Классический пример классического определения.
2. 3 Геометрическая и статистическая вероятности.
3. Простейшие статистические понятия.
3. 1 Задачи математической статистики.
3. 2 Математическое ожидание, мода, медиана.
1. Основы комбинаторики.
1. 1 Комбинаторика – раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, можно скомбинировать из заданных объектов; раздел математики, который занят поисками ответов на вопросы: сколько всего есть комбинаций в том или ином случае, как из всех этих комбинаций выбрать наилучшую.
Долгие времена комбинаторика развивалась в глубинах
арифметики, геометрии, алгебры. Однако как ветвь математики комбинаторика возникла только в XVII веке. Комбинаторику как самостоятельный раздел математики первым стал рассматривать выдающийся немецкий учёный Готфрид Вильгельм Лейбниц в своей работе < < Об искусстве комбинаторики> >, опубликованной в 1666 году (Здесь же он вводит термин < < комбинаторика> > ).
Простые задачи решают обыкновенным полным перебором возможных вариантов без составления различных таблиц и схем. В таких задачах нужно внимательно прочитать условие задачи и выписать все нужные комбинации, а затем посчитать их количество и дать ответ.
Пример 1. Сколько двузначных чисел можно скомбинировать, имея три цифры 3; 5; 9? (цифры могут повторяться)
Пример 2. Сколько найдется двухзначных чисел, скомбинированных из цифр: 0, 5, 8, если нельзя использовать повторение цифр?
Полный перебор – метод решения математических задач. Принадлежит к классу методов отыскания решений перечислением всех возможных вариантов. Сложность полного перебора обусловливаться количеством всевозможных решений задачи. Если решений будет очень много, то школьникам будет не интересно считать такие задачи, поэтому рекомендуется брать простые задачи. Важно, чтоб ребята понимали, что этот метод решения не единственный. В дальнейшем при изучении нового материала необходимо возвращаться к этому методу.
Решение многих комбинаторных задач основывается на двух фундаментальных правилах, называемых правилом суммы и правилом произведения. Прежде всего, определимся в терминологии. Если имеется, к примеру, 5 шаров в ящике, то мы будем говорить, что один шар из ящика можно выбрать пятью способами. Правила суммы и произведения справедливы не только для двух, но и для любого числа объектов.
Пример 3. Сколько может быть различных комбинаций выпавших граней при бросании двух игральных костей? (Игральная кость --- это кубик, на гранях которого нанесены числа 1, 2, 3, 4, 5, 6)
Пример 4. В корзинке лежат 6 бананов и 3 апельсина. Сколькими способами можно выбрать пару плодов, состоящую из банана и апельсина?
Пример 5. У пекаря имеется 12 цветов. Пекарь выбирает цвета для окраски мастики для изготовления двух фигурок разных цветов. Сколькими способами это можно сделать?
1. 2 Размещениями из n элементов по k 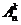 называются всевозможные комбинации по k элементов, составленные из элементов данных n видов. При этом две комбинации считаются различными, если они либо отличаются друг от друга хотя бы одним элементом, либо состоят из одних и тех же элементов, но расположенных в разном порядке.
называются всевозможные комбинации по k элементов, составленные из элементов данных n видов. При этом две комбинации считаются различными, если они либо отличаются друг от друга хотя бы одним элементом, либо состоят из одних и тех же элементов, но расположенных в разном порядке.
Примеры
Перестановками из n элементов называют всевозможные комбинации из n элементов, каждая из которых содержит все элементы по одному разу. [9] Комбинации отличаются друг от друга лишь порядком элементов.
Примеры
Сочетаниями из n элементов по k ( 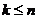 ) называют всевозможные комбинации по k элементов, составленные из данных n элементов. Комбинации отличаются друг от друга только по составу, но не порядком элементов. Число сочетаний из n по k обозначается
) называют всевозможные комбинации по k элементов, составленные из данных n элементов. Комбинации отличаются друг от друга только по составу, но не порядком элементов. Число сочетаний из n по k обозначается 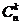 .
.
Примеры
1. 3 Основной закон комбинаторики
Пример. В волейбольной секции 9 человек. Они ходили на тренировки нерегулярно. Сколько всего различных вариантов прихода на тренировку?
Примечание. Задачу рассмотреть двумя способами и подвести к основному закону комбинаторики.
2. Элементы теории вероятностей.
2. 1 Элементарное событие. Пространство элементарных событий.
Событие A – подмножество пространства элементарных событий.
Достоверное событие, как множество, совпадающее с пространством элементарных событий. Понятие невозможного события.
Пример 1. Бросание монеты: однократное, двукратное, многократное, по определенному правилу.
Пример 2. Бросание кубика: однократное, двукратное, многократное, по определенному правилу.
2. 2 Классическое определение вероятности с использованием понятия вероятности элементарного события:
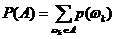 , где
, где 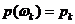 - вероятности элементарных исходов, благоприятствующих событию А.
- вероятности элементарных исходов, благоприятствующих событию А.
Свойства
1. 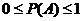
2. 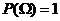
3. 
Пример: бросание монеты до первого выпадения Герба.
Классический пример классической вероятности – все события равновероятны и их конечное число.
2. 3 Геометрическая и статистическая вероятности.
Необходимость рассмотрения других определений вероятности.
Геометрическая вероятность события, как отношение длин (площадей, объемов).
Пример 1. Бросание монеты на разграфленный стол.
Геометрическая вероятность в негеометрических задачах.
Пример 2. Задача о встрече.
Статистическое представление о вероятности.
Задачи о большом числе опытов, проводимых в одинаковых условиях.
3. Простейшие статистические понятия.
3. 1 Задачи математической статистики.
Примеры практико-ориентированных задач, связанных с математической статистикой
Пример 1
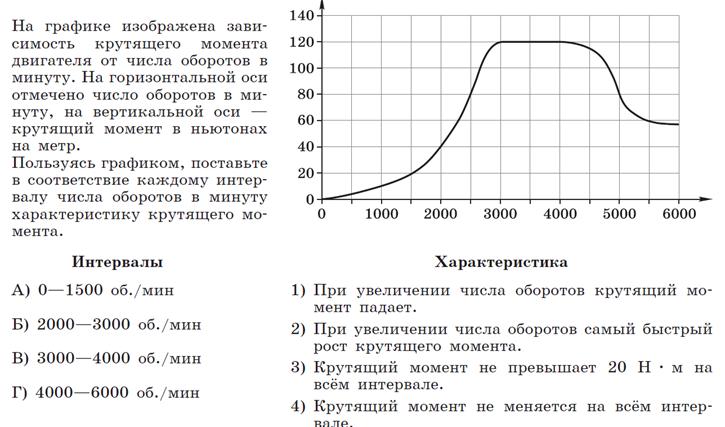
Пример 2
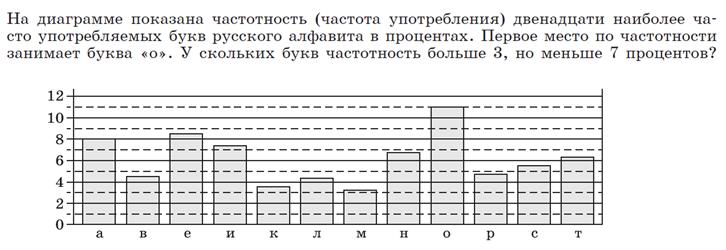
3. 2 Математическое ожидание, мода, медиана.
Математическим ожиданием называется среднее арифметическое всех значений совокупности:

(немного упрощено для школьников).
Мода 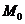 дискретного вариационного ряда – это варианта с максимальной частотой.
дискретного вариационного ряда – это варианта с максимальной частотой.
Медиана  вариационного ряда – это значение, которая делит его на две равные части (по количеству вариант). То есть, медиана – это варианта, которая находится в середине упорядоченного вариационного ряда.
вариационного ряда – это значение, которая делит его на две равные части (по количеству вариант). То есть, медиана – это варианта, которая находится в середине упорядоченного вариационного ряда.
Пример.
Рассмотрим расчет моды и медианы в дискретном вариационном ряду:
| Стаж, лет, X | Число рабочих, чел, f | Накопленные частоты |
| (11) | ||
| ИТОГО: | - |
Определить моду и медиану.
Мода Мо= 4 года, так как этому значению соответствует наибольшая частота f = 5.
Т. е. наибольшее число рабочих имеют стаж 4 года.
Для того, чтобы вычислить медиану, найдем предварительно половину суммы частот. Если сумма частот является числом нечетным, то мы сначала прибавляем к этой сумме единицу, а затем делим пополам:
Ме=16/2=8
Медианой будет восьмая по счету варианта.
Для того, чтобы найти, какая варианта будет восьмой по номеру, будем накапливать частоты до тех пор, пока не получим сумму частот, равную или превышающую половину суммы всех частот. Соответствующая варианта и будет медианой.
Ме= 4 года.
Т. е. половина рабочих имеет стаж меньше четырех лет, половина больше.
Литература
1. Генкин С. А., Итенберг И. В., Фомин Д. В. Ленинградские математические кружки. — Киров: АСА, 1994. — 272 с.
2. Яглом А. М., Яглом И. М. Неэлементарные задачи в элементарном изложении. М., ГТТИ, 1954. — 554с. (Выпуск 5 серии " Библиотека математического кружка" )
3. Сайт «Решу ОГЭ (ЕГЭ)» http: //math-ege. sdamgia. ru, math-oge. sdamgia. ru
4. Конспект урока по алгебре ≪ Комбинаторные задачи≫ 9–10 класс. [Электронный ресурс] — Режим доступа: https: //doc4web. ru/algebra/konspekt-uroka-po-algebrekombinatornie-zadachi-klass. html
5. Комбинаторные задачи. [Электронный ресурс] — Режим доступа:
http: //pandia. ru/text/77/415/82046. php
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|