
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема занятия: Дифференцирование функций
Тема занятия: Дифференцирование функций
Задания:
1) внимательно просмотрите видеоролики
Вычисление производных: https: //www. youtube. com/watch? v=v4_kYEpKwjc
Производная сложной функции: https: //www. youtube. com/watch? v=jcGiIx6B97A
Дифференциал функции: https: //www. youtube. com/watch? v=WKZzfpGiHK4
Приближенные вычисления с помощью дифференциала: https: //www. youtube. com/watch? v=DLDnWzvm1Vo
2) ответьте устно на вопросы:
- Что означает термин «приращение»? Как найти приращение аргумента? Как найти приращение функции?
- Что называется производной функции в точке? Как называется действие нахождения производной?
- Как обозначается производная функции?
- Чему равна производная алгебраической суммы нескольких функций?
- Как вычислить производную произведения? Как вычислить производную частного?
- Какая функция называется сложной? Как найти производную сложной функции?
- Что называется дифференциалом функции? Как обозначается дифференциал функции?
3) выпишите формулы и правила вычисления производных;
4) выполните задания практической части работы.
Скан решения направлять в личном сообщении
Практическая часть
1. Вычислите производную функции:
а)  б)
б)  в)
в) 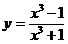
2. Найдите производную функции y=f(x) и вычислить ее значение в точке х0:
а)  , х0=2 б)
, х0=2 б) 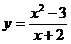 , х0= -1
, х0= -1
3. Найдите производную сложной функции:
а)  б)
б)  в)
в) 
4. Найдите дифференциалы следующих функций:



5. Вычислить значение дифференциала следующих функций:
 , если х=2,
, если х=2, 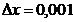
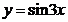 , если
, если 
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|